Ermitteln Sie die Gleichung der Tangente an \(G_h\) im Punkt \((-2|h(-2))\). Berechnen Sie den Wert, den das Modell für die Größe des Winkels liefert, den die Blattränder an der Blattspitze einschließen.
(6 BE)
Lösung zu Teilaufgabe 3b
Gleichung der Tangente an \(G_h\) im Punkt \((-2|h(-2))\)
1. Lösungsansatz: Allgemeine Geradengleichung
\[h(x) = -\frac{1}{2}x^2 + 2x + 4\,; \quad D = \mathbb R\]
\(S_{1}\,(-2|-2)\enspace\) (siehe Teilaufgabe 2a)
Allgemeine Geradengleichung
\[y = mx + t\]
Wobei \(m\) die Steigung und \(t\) der \(y\)-Achsenabschnitt der Geraden ist.
\[T\,\colon\,y = m_{T} \cdot x + t\]
Steigungsfaktor \(m_{T}\) der Tangente \(T\) berechnen:
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[m_{T} = h'(-2)\]
Erste Ableitung \(h'\) bilden:
\[h(x) = -\frac{1}{2}x^2 + 2x + 4\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[\begin{align*}h'(x) &= -\frac{1}{2} \cdot 2 \cdot x + 2 \\[0.8em] &= -x + 2\end{align*}\]
\[m_{T} = h'(-2) = -(-2) + 2 = 4\]
\(y\)-Achsenabschnitt \(t\) berechnen:
\[T\,\colon\,y = 4x + t\]
\[S_{1}\,(-2|-2)\]
\[\begin{align*} S_{1} \in T\,\colon\, -2 &= 4 \cdot (-2) + t \\[0.8em] -2 &= -8 + t & &| +8 \\[0.8em] 6 &= t \end{align*}\]
\[\Longrightarrow \quad T\,\colon\,y = 4x + 6\]
2. Lösungansatz: Tangentengleichung
\[h(x) = -\frac{1}{2}x^2 + 2x + 4\,; \quad D = \mathbb R\]
\(S_{1}\,(-2|-2)\enspace\) (siehe Teilaufgabe 2a)
Gleichung einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\;(x_0|f(x_0)) \):
\[y = f'(x_{0}) \cdot (x - x_{0}) + f(x_{0})\]
\[T\,\colon\, y = h'(x_{0}) \cdot (x - x_{0}) + h(x_{0})\]
Erste Ableitung \(h'\) bilden:
\[h(x) = -\frac{1}{2}x^2 + 2x + 4\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[\begin{align*}h'(x) &= -\frac{1}{2} \cdot 2 \cdot x + 2 \\[0.8em] &= -x + 2\end{align*}\]
\[h'(x_{0}) = h'(-2) = -(-2) + 2 = 4\]
Gleichung der Tangente aufstellen:
\[\begin{align*}y &= h'(x_{0}) \cdot (x - x_{0}) + h(x_{0}) \\[0.8em] &= 4 \cdot (x - (-2)) + (-2) \\[0.8em] &= 4x + 8 - 2 \\[0.8em] &= 4x + 6\end{align*}\]
\[\Longrightarrow \quad T\,\colon\,y = 4x + 6\]
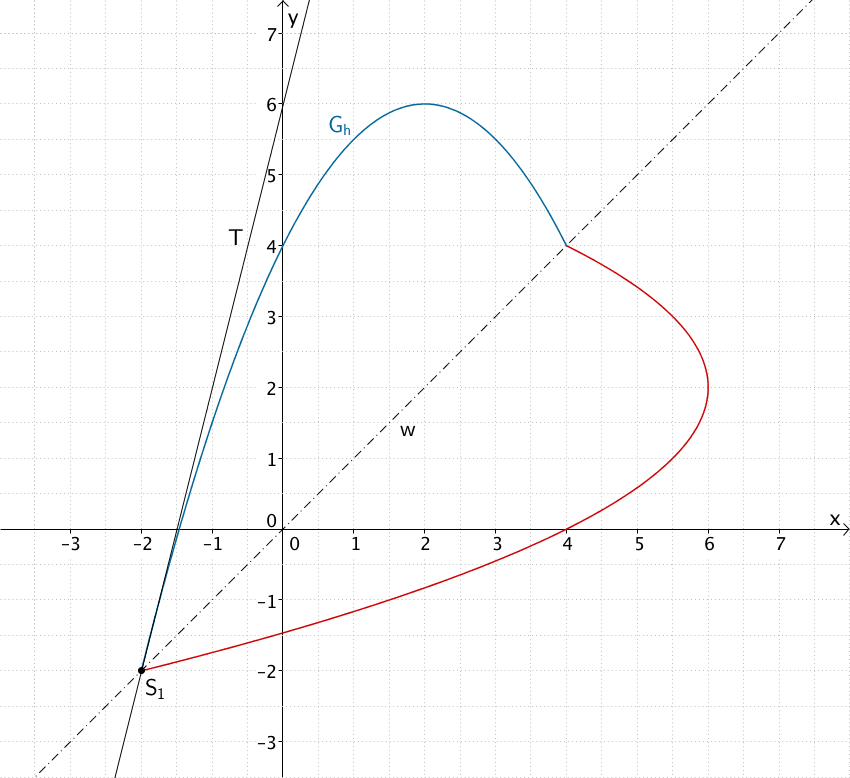
Tangente \(T\) an \(G_h\) im Punkt \(S_{1}(-2|-2)\)
Wert, den das Modell für die Größe des Winkels liefert, den die Blattränder an der Blattspitze einschließen
Es sei \(\varphi\) das Maß des Winkels, den die Blattränder im Modell an der Blattspitze einschließen.
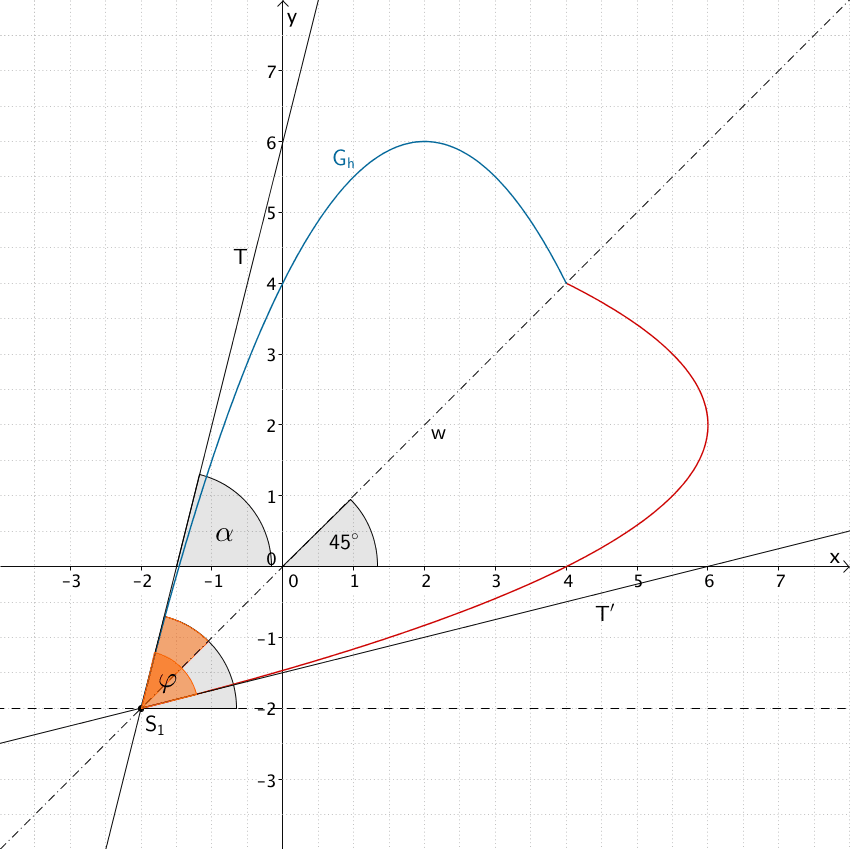
Der Winkel \(\varphi\), den die Blattränder im Modell an der Blattspitze einschließen, ist gleich dem spitzen Winkel, den die Tangente \(T\) und die an der Winkelhalbierenden \(w\) gespiegelte Bildtangente \(T'\) einschließen. Der Wert des Winkels \(\varphi\) lässt sich mithilfe des Steigungswinkel \(\alpha\) der Tangente \(T\) berechnen.
\[\varphi = 2 \cdot (\alpha - 45^{\circ})\]
Steigungswinkel \(\alpha\) der Tangente \(T\) berechnen:
Steigungswinkel \(\alpha\) einer Gerade \(g \colon y = m \cdot x +t\)
\[\tan \alpha = m \qquad \alpha \neq 90^\circ\]
\[m_{T} = 4\enspace\]
\[\begin{align*}\tan{\alpha} &= m_{T} \\[0.8em] \tan{\alpha} &= 4 & &| \; \tan^{-1}(\dots) \\[0.8em] \alpha &\approx 75{,}96^{\circ}\end{align*}\]
Winkel \(\varphi\) berechnen:
\[\begin{align*}\varphi &= 2 \cdot (\alpha - 45^{\circ}) \\[0.8em] &= 2 \cdot (75{,}96^{\circ}- 45^{\circ}) \\[0.8em] &= 61{,}92^{\circ}\end{align*}\]
Die Größe des Winkels, den die Blattränder im Modell an der Blattspitze einschließen, beträgt 61,92°.

