Bestimmen Sie die Koordinaten zweier Punkte \(C\) und \(D\) so, dass \(C\) auf \(h\) liegt und das Viereck \(ABCD\) eine Raute ist.
(4 BE)
Lösung zu Teilaufgabe b
Ein Raute ist ein Viereck mit vier gleich langen Seiten, von denen jeweils zwei gegenüberliegende zueinander parallel sind (Parallelogramm mit vier gleich langen Seiten).
(vgl. Abiturskript - 2.1.6 Nachweis von Vierecken, spezielle Vierecke)
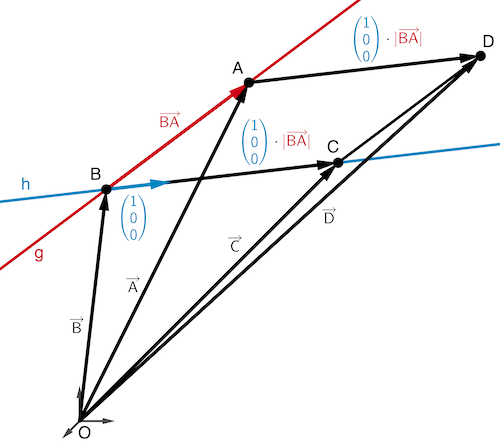
Planskizze (schematisch, optional): Der Punkt \(C\) soll auf der Gerade \(h\) liegen. Damit das Viereck \(ABCD\) eine Raute ist, muss \(\overline{BC} = \overline{BA}\) gelten.
Da der Richtungsvektor \(\textcolor{#0087c1}{\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}}\) von \(\textcolor{#0087c1}{h}\) ein Einheitsvektor der Länge \(1\) ist, ergibt die Vektoraddition \(\overrightarrow{B} + \textcolor{#0087c1}{\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}} \cdot \textcolor{#cc071e}{\vert \overrightarrow{BA} \vert}\) den Ortsvektor des Punktes \(C\).
Und mit \([AD] \parallel [BC]\) errechnet die Vektoraddition \(\overrightarrow{A} + \textcolor{#0087c1}{\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}} \cdot \textcolor{#cc071e}{\vert \overrightarrow{BA} \vert}\) den Ortsvektor des Punktes \(D\).
Länge (Betrag) des Verbindungsvektor \(\overrightarrow{BA}\) berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\(A(3|5|5)\), \(B(1|1|1)\)
\[\begin{align*}\textcolor{#cc071e}{\vert \overrightarrow{BA} \vert} &= \vert\overrightarrow{A} - \overrightarrow{B}\vert = \left| \begin{pmatrix} 3\\5\\5 \end{pmatrix} - \begin{pmatrix} 1\\1\\1 \end{pmatrix}\right| = \left| \begin{pmatrix} 2\\4\\4 \end{pmatrix} \right| \\[0.8em] &= \sqrt{2^2 + 4^2 + 4^2} = \sqrt{36} = \textcolor{#cc071e}{6} \end{align*}\]
Koordinaten der Punkte \(C\) und \(D\) bestimmen:
\[\overrightarrow{C} = \overrightarrow{B} + \textcolor{#0087c1}{\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}} \cdot \textcolor{#cc071e}{\vert \overrightarrow{BA} \vert} = \begin{pmatrix} 1\\1\\1 \end{pmatrix} + \textcolor{#0087c1}{\begin{pmatrix}1\\0\\0 \end{pmatrix}} \cdot \textcolor{#cc071e}{6} = \begin{pmatrix}7\\1\\1 \end{pmatrix}\]
\[\Rightarrow \, C(7|1|1)\]
\[\overrightarrow{D} = \overrightarrow{A} + \textcolor{#0087c1}{\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}} \cdot \textcolor{#cc071e}{\vert \overrightarrow{BA} \vert} = \begin{pmatrix} 3\\5\\5 \end{pmatrix} + \textcolor{#0087c1}{\begin{pmatrix}1\\0\\0 \end{pmatrix}} \cdot \textcolor{#cc071e}{6} = \begin{pmatrix}9\\5\\5 \end{pmatrix}\]
\[\Rightarrow \, D(9|5|5)\]


