Aufgabe 1
Gegeben ist die Funktion \(f\) mit \(f(x) = -\dfrac{3}{x - 2}\).
a) Bestimmen Sie \(\lim \limits_{x\,\to\,-\infty}f(x)\) und \(\lim \limits_{x\,\to\,+\infty}f(x)\). Beschreiben Sie Ihre Ergebnisse in Worten und interpretieren Sie diese graphisch.
b) Der Graph der Funktion \(g\) geht aus dem Graphen der Funktion \(f\) durch Verschiebung in \(x\)-Richtung und in \(y\)-Richtung hervor, wobei er die Asymptoten mit den Gleichungen \(x = 3\) und \(y = -2\) besitzt. Geben Sie die zugehörige Verschiebung in \(x\)-Richtung und in \(y\)-Richtung an sowie einen Funktionsterm von \(g\).
c) Der Graph der Funktion \(h\) entsteht aus dem Graphen der Funktion \(f\) durch eine Streckung mit dem Faktor 3 in \(y\)-Richtung und eine anschließende Verschiebung um 2 in \(y\)-Richtung. Der Graph der Funktion \(k\) entsteht aus dem Graphen der Funktion \(f\) durch die angegebene Streckung und Verschiebung in umgekehrter Reihenfolge. Entscheiden Sie, ob folgende Aussage richtig ist: „Die Funktionsterme von \(h\) und \(k\) unterscheiden sich." Begründen Sie ihre Entscheidung.
Aufgabe 2
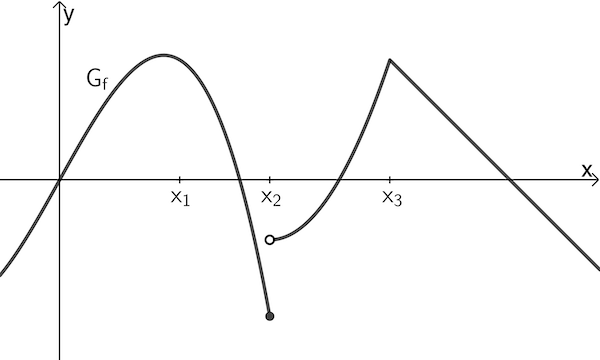
a) Die Abbildung zeigt den Graphen einer Funktion \(f\). Erläutern Sie anhand des Graphen, ob die Funktion \(f\) an den Stellen \(x_1\), \(x_2\) und \(x_3\) jeweils stetig ist.
b) Gegeben ist die Funktion
\[g \colon x \mapsto \begin{cases} \begin{align*} &ax + a &&\text{für} \; x < 1 \\[0.8em] &-2 &&\text{für}\;1 \leq x < 5 \\[0.8em] &b \cdot (x^3 - 10x^2 + 25x)-2 &&\text{für}\;x \geq 5 \end{align*} \end{cases}\enspace\text{mit}\;a, b \in \mathbb R\]
Bestimmen Sie den Wert von \(a\) so, dass \(g\) an der Stelle \(x = 1\) stetig ist und zeigen Sie, dass \(g\) an der Stelle \(x = 5\) unabhängig vom Wert von \(b\) stetig ist.
Aufgabe 3
Gegeben ist die Funktion \(f \colon x \mapsto \dfrac{x(x-3)}{(x-2)^2}\) mit maximaler Definitionsmenge \(D_f\).
a) Geben Sie \(D_f\) an und entscheiden Sie, welcher der Graphen I bis IV den Graphen der Funktion \(f\) darstellt. Begründen Sie Ihre Entscheidung.
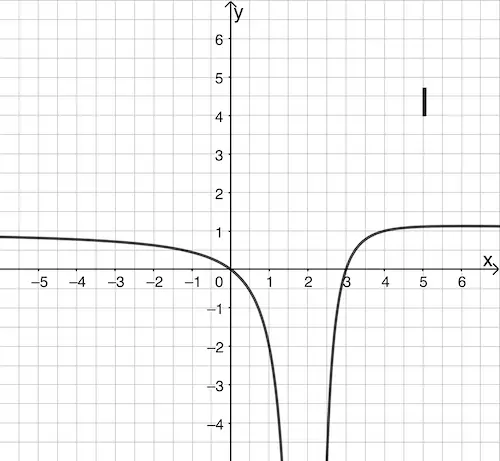
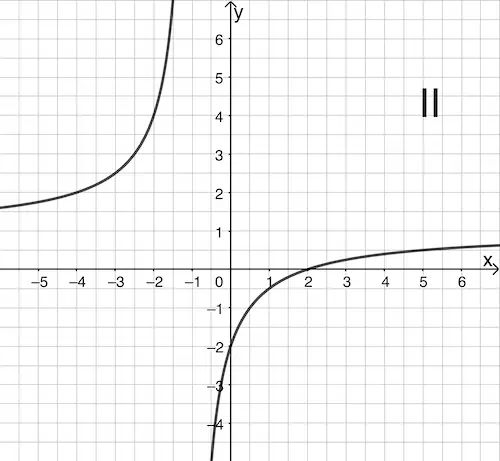
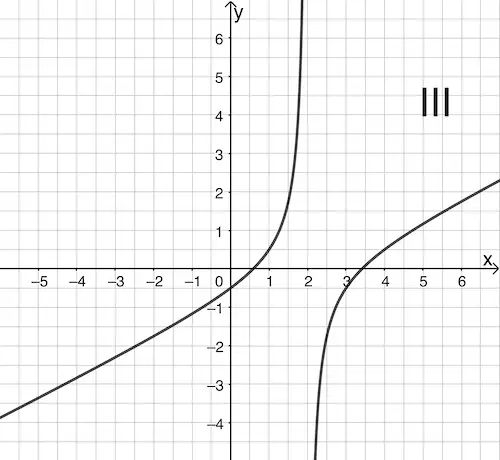
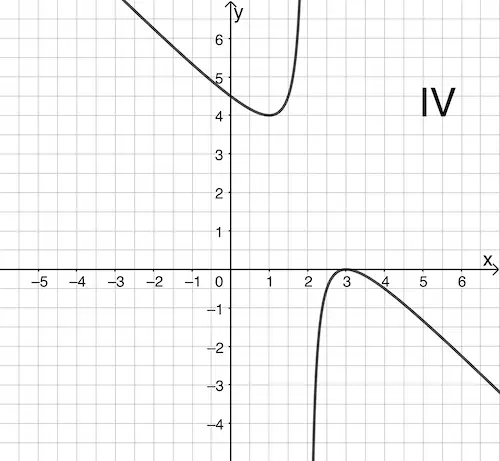
b) Graph IV zeigt den Graphen einer gebrochenrationalen Funktion \(g\), der eine schräge Asymptote mit der Gleichung \(y = -x + 4\) besitzt. Die Koordinaten der Schnittpunkte des Graphen von \(g\) mit den Koordinatenachsen sowie die Polstelle von \(g\) sind ganzzahlig.
Geben Sie an, welcher der folgenden Funktionsterme die Funktion \(g\) beschreibt.
\[\text{A}\quad\frac{1}{x - 2} -x +4\]
\[\text{B}\quad-\frac{1}{x-2} -x +4\]
\[\text{C}\quad\frac{1}{2-x} +x - 4\]
\[\text{D}\quad\frac{1}{2-x}-x-4\]
Aufgabe 4
Gegeben ist die gebrochenrationale Funktion \(f \colon x \mapsto \dfrac{-2x-4}{x^3+6x^2+9x}\) mit maximaler Definitionsmenge \(D_f\). Der Graph von \(f\) wird mit \(G_f\) bezeichnet.
a) Geben Sie die Nullstelle von \(f\) an. Untersuchen Sie \(f\) auf Polstellen und geben Sie \(D_f\) an. Bestimmen Sie das Verhalten von \(G_f\) an den Definitionslücken.
b) Untersuchen Sie \(G_f\) auf schräge oder waagrechte Asymptoten.
c) Berechnen Sie \(f(-4)\) und \(f(1)\) und zeichnen Sie \(G_f\) im Bereich \(-7 < x < 4\) in ein Koordinatensystem.
Aufgabe 5
a) Bestimmen Sie den Grenzwert \(\lim \limits_{x\,\to\,2} f(x)\) mit \(f(x) = \dfrac{4x^2-6x-4}{x-2}\).
(Zwischenergebnis: \(x = 2\) ist Nullstelle von \(f\))
b) Die Grenzwertbetrachtung lässt auf eine besondere Eigenschaft der gebrochrationalen Funktion \(f\) schließen. Geben sie diese an und beschreiben Sie kurz wie sich der Graph von \(f\) an der Stelle \(x = 2\) verhält.
Aufgabe 6
Beim Fernsehsender „Sport TV" treten bei Live-Übertragungen mit einer Wahrscheinlichkeit von 4 % Bildstörungen auf. Wenn das Bild gestört ist, kommt es mit einer Wahrscheinlichkeit von 60 % auch zu Tonstörungen. Bei 13,6 % der Übertragungen kommt es zu Bild- oder Tonstörungen.
Betrachte werden folgende Ereignisse:
\(B\): „Es tritt eine Bildstörung bei der Live-Übertragung auf",
\(T\): „Es tritt eine Tonstörung bei der Live-Übertragung auf".
a) Zeigen Sie, dass bei 12 % aller Live-Übertragungen Tonstörungen auftreten.
b) Berechnen Sie die Wahrscheinlichkeit dafür, dass bei einer Live-Übertragung
- ein einwandfreies Bild empfangen wird, falls der Ton gestört ist.
- Bild oder Ton einwandfrei empfangen werden.
c) Untersuchen Sie, ob die Ereignisse \(B\) und \(T\) stochastisch unabhängig sind.


