Die in \(\mathbb R\) definierte Funktion \(f\) besitzt die Nullstelle \(x = 2\), außerdem gilt \(f'(x) > 0\) für alle \(x \in \mathbb R\). Abbildung 2 zeigt den Graphen \(G_f\) von \(f\).
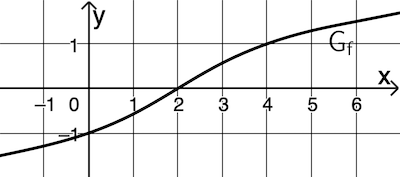
Betrachtet wird die Funktion \(g \colon x \mapsto \ln{\left( f(x) \right)}\) mit maximaler Definitionsmenge \(D_g\). Geben Sie \(D_g\) an und ermitteln Sie mithilfe von Abbildung 2 diejenige Stelle \(x\), für die \(g'(x) = f'(x)\) gilt.
(3 BE)
Lösung zu Teilaufgabe 3b
\[g(x) = \ln{\left( f(x) \right)}\]
Maximale Definitionsmenge \(D_g\)
\[D_g = ]2;+\infty[\]
Begründung (nicht verlangt)
Die natürliche Logarithmusfunktion ist in \(\mathbb R^+\) definiert. Deshalb muss im Falle der Funktion \(g(x) = \ln{\left( f(x) \right)}\) gelten: \(\textcolor{#0087c1}{f(x) > 0}\).
Maximale Definitionsmenge bestimmen
Gebrochenrationale Funktion / Quotient von Funktionen
\[x \mapsto \dfrac{Zähler(x)}{\textcolor{#e9b509}{\underbrace{Nenner(x)}_{\Large{\neq \, 0}}}}\]
Nullstelle(n) des Nenners ausschließen!
Wurzelfunktion
\[x \mapsto \sqrt{\mathstrut\smash{\textcolor{#e9b509}{\underbrace{\dots}_{\Large{\geq\,0}}}}} \\ {}\]
Der Wert des Terms unter der Wurzel (Radikand ) darf nicht negativ sein!
(natürliche) Logarithmusfunktion
\(x \mapsto \ln{(\,\textcolor{#e9b509}{\underbrace{\dots}_{\Large{>\,0}}}\,)}\) bzw. \(x \mapsto \log_{a}{(\,\textcolor{#e9b509}{\underbrace{\dots}_{\Large{>\,0}}}\,)}\)
Die (Natürliche) Logarithmusfunktion ist in \(\textcolor{#e9b509}{\mathbb R^{+}}\) definiert!
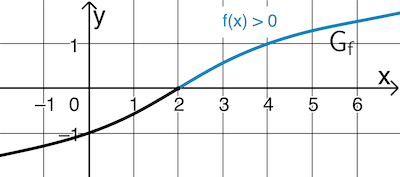Abb. 2
Im Bereich \(x > 2\) verläuft \(G_f\) oberhalb der \(\textcolor{#0087c1}{x}\)-Achse, d. h. es gilt \(\textcolor{#0087c1}{f(x) > 0}\) für \(x \in \; ]2;+\infty[\).
Somit ist \(D_g =\; ]2;+\infty[\) der maximale Definitionsbereich der Funktion \(g\).
Stelle, für die \(g'(x) = f'(x)\) gilt, mithilfe von Abbildung 2 ermitteln
Mithilfe der Ableitungsfunktion \(g'\) gelingt es, die Gleichung \(g'(x) = f'(x)\) in eine Bedingung für \(f(x)\) umzuformen.
Erste Ableitung \(g'\) bilden:
Hierfür wird die Kettenregel benötigt.
\[g(x) = \textcolor{#0087c1}{\ln{\left( \textcolor{#cc071e}{f(x)} \right)}}; \; D_g = \; ]2;+\infty[\]
Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
vgl. Merkhilfe
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
vgl. Merkhilfe
\[g'(x) = \textcolor{#0087c1}{\frac{1}{\textcolor{#cc071e}{f(x)}}} \cdot \textcolor{#cc071e}{f'(x)} = \frac{f'(x)}{f(x)}\]
Somit folgt:
\[\begin{align*}g'(x) &= f'(x) \\[0.8em] \frac{f'(x)}{f(x)} &= f'(x) &&| : f'(x) \; \text{mit}\; f'(x) > 0\;\text{(vgl. Angabe)} \\[0.8em] \frac{1}{f(x)} &= 1 &&| \cdot f(x) \\[0.8em] \textcolor{#cc071e}{1} &\textcolor{#cc071e}{=} \textcolor{#cc071e}{f(x)} \end{align*}\]
Anmerkung:
Die Angabe \(f'(x) > 0\) ist für die Lösung der Gleichung entscheidend, da andernfalls \(f'(x) =0\) als Lösung der Gleichung berücksichtigt werden müsste.
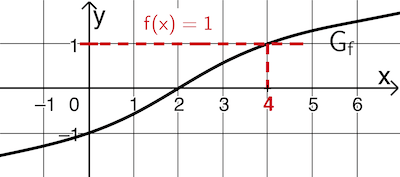Abb. 2
Mithilfe von Abbildung 2 ergibt sich \(\textcolor{#cc071e}{f(4) = 1}\). Damit ist \(x = 4\) diejenige Stelle, für die \(g'(x) = f'(x)\) gilt.
