In einem Modell für einen Küstenabschnitt am Meer beschreibt die \(x_1x_2\)-Ebene die horizontale Wasseroberfläche und die Gerade \(g\) die Uferlinie. Die Ebene \(E\) stellt im betrachteten Abschnitt den Meeresboden dar. Eine Boje schwimmt auf der Wasseroberfläche an der Stelle, die dem Koordinatenursprung \(O\) entspricht (vgl. Abbildung). Eine Längeneinheit entspricht einem Meter in der Realität.
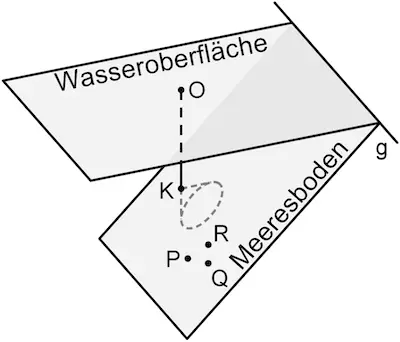
Bestimmen Sie die Größe des Winkels, unter dem der Meeresboden gegenüber der Wasseroberfläche abfällt.
(3 BE)
Lösung zu Teilaufgabe d
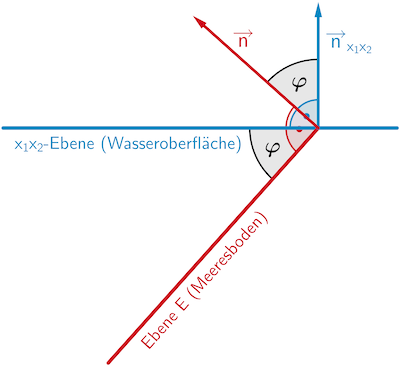
Die Größe des Winkels, unter dem der Meeresboden gegenüber der Wasseroberfläche abfällt, entspricht im Modell der Größe des Schnittwinkels \(\varphi\) zwischen der \(\textcolor{#0087c1}{x_1x_2}\)-Ebene und der Ebene \(\textcolor{#cc071e}{E}\). Der Schnittwinkel der Ebenen ist gleich dem Winkel zwischen den Normalenvektoren der Ebenen (Skizze schematisch, nicht verlangt).
\(\textcolor{#0087c1}{\overrightarrow{n}_{x_1x_2} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}}\) ist ein Normalenvektor der \(\textcolor{#0087c1}{x_1x_2}\)-Ebene.
\(\textcolor{#cc071e}{\overrightarrow{n} = \begin{pmatrix} 2 \\ -1 \\ 2 \end{pmatrix}}\) ist ein Normalenvektor der Ebene \(\textcolor{#cc071e}{E}\) (vgl. Teilaufgabe b).
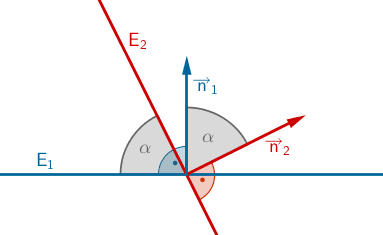
Schnittwinkel \(\boldsymbol{\alpha}\) zweier Ebenen
\[E_1\colon \enspace \overrightarrow{n}_1 \circ \left( \overrightarrow{X} - \overrightarrow{A} \right) = 0\]
\[E_2\colon \enspace \overrightarrow{n}_2 \circ \left( \overrightarrow{X} - \overrightarrow{B} \right) = 0\]
\[\cos \alpha = \frac{\vert \overrightarrow{n}_1 \circ \overrightarrow{n}_2 \vert}{\vert \overrightarrow{n}_1 \vert \cdot \vert \overrightarrow{n}_2 \vert} \enspace \Rightarrow \enspace \alpha = \cos^{-1}(\dots)\]
\[(0^{\circ} \leq \alpha \leq 90^{\circ})\]
\[\begin{align*} \cos{\varphi} &= \frac{\vert \textcolor{#0087c1}{\overrightarrow{n}_{x_1x_2}} \circ \textcolor{#cc071e}{\overrightarrow{n}}\vert}{\vert \textcolor{#0087c1}{\overrightarrow{n}_{x_1x_2}} \vert \cdot \vert \textcolor{#cc071e}{\overrightarrow{n}} \vert} = \frac{\left| \textcolor{#0087c1}{\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}} \circ \textcolor{#cc071e}{\begin{pmatrix} 2 \\ -1 \\ 2 \end{pmatrix}} \right|}{\left| \textcolor{#0087c1}{\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}} \right| \cdot \left| \textcolor{#cc071e}{\begin{pmatrix} 2 \\ -1 \\ 2 \end{pmatrix}} \right|} \\[0.8em] &= \frac{\vert \textcolor{#0087c1}{0} \cdot \textcolor{#cc071e}{2} + \textcolor{#0087c1}{0} \cdot \textcolor{#cc071e}{(-1)} + \textcolor{#0087c1}{1} \cdot \textcolor{#cc071e}{2} \vert}{\sqrt{\textcolor{#0087c1}{0}^2 + \textcolor{#0087c1}{0}^2 + \textcolor{#0087c1}{1}^2} \cdot \sqrt{\textcolor{#cc071e}{2}^2 + \textcolor{#cc071e}{(-1)}^2 + \textcolor{#cc071e}{2}^2}} \\[0.8em] &= \frac{2}{1 \cdot 3} = \frac{2}{3} &&| \; \text{TR:}\; \cos^{-1}(\dots) \\[2.4em] \varphi &= \cos^{-1}\left( \frac{2}{3} \right) \approx 48{,}2^{\circ}\end{align*}\]


