Bedingte Wahrscheinlichkeit
Bei der Betrachtung zweier Ereignisse \(A\) und \(B\) eines Zufallsexperiments müssen folgende beiden Fälle sorgfältig unterschieden werden:
Es interessiert die Wahrscheinlichkeit dafür, dass die Ereignisse \(A\) und \(B\) zugleich eintreten.
Es interessiert die Wahrscheinlichkeit dafür, dass das Ereignis \(B\) unter der Voraussetzung eintritt, dass das Ereignis \(A\) bereits eingetreten ist (oder umgekehrt). Diese Wahrscheinlichkeit wird als bedingte Wahrscheinlichkeit von \(\boldsymbol{B}\) unter der Bedingung \(\boldsymbol{A}\) bezeichnet.
Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit für das Eintreten des Ereignisses \(B\) unter der Voraussetzung oder der Bedingung, dass das Ereignis \(A\) bereits eingetreten ist, heißt bedingte Wahrscheinlichkeit von \(\boldsymbol{B}\) unter der Bedingung \(\boldsymbol{A}\) und wird durch die Schreibweise \(P_{A}(B)\) gekennzeichnet.
Es gilt: \(P_{A}(B) = \dfrac{P(A \cap B)}{P(A)} \quad (P(A) \neq 0)\)
(vgl. Merkhilfe)
Bedingte Wahrscheinlichkeit und Baumdiagramm
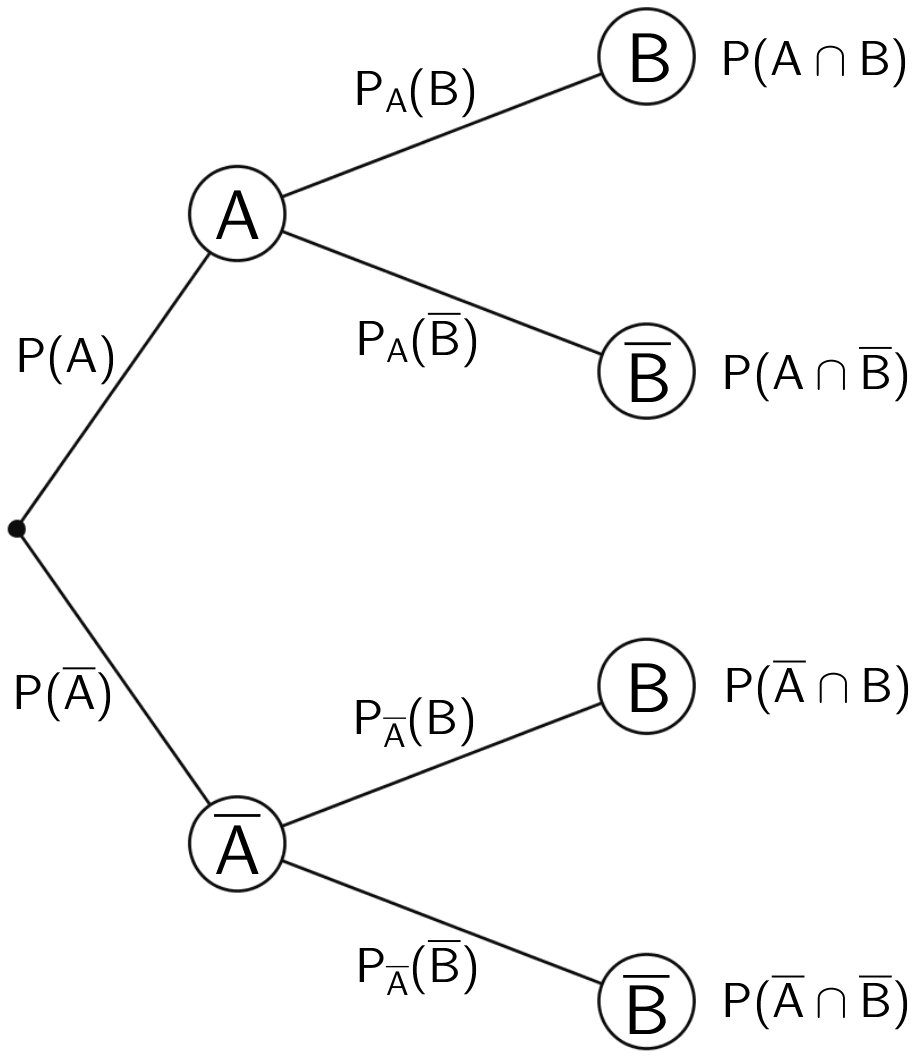
Die bedingten Wahrscheinlichkeiten werden bei einem Baumdiagramm an den Pfaden der zweiten Stufe (oder höher) angetragen.
Treten an den Pfaden der zweiten Stufe (oder höher) die gleichen Wahrscheinlichkeiten auf, gilt also beispielsweise \(P_{A}(B) = P_{\overline{A}}(B) = P(B)\), so sind die Ereignisse \(A\) und \(B\) unabhängig (vgl. Abiturskript - 3.1.6 Unabhängigkeit von Ereignissen).
An den Enden der Pfade eines Baumdiagramms stehen die Wahrscheinlichkeiten für das gleichzeitige Eintreten von Ereignissen.
Bedingte Wahrscheinlichkeit und Vierfeldertafel
Die bedingten Wahrscheinlichkeiten ergeben sich bei einer Vierfeldertafel als Quotient aus dem Eintrag einer inneren Zelle und dem Eintrag einer Randzelle.
Beispiele:
\[P_{A}(B) = \frac{P(A \cap B)}{P(A)}\]
\[P_{B}(A) = \frac{P(A \cap B)}{P(B)}\]
| \(A\) | \(\overline{A}\) | ||
| \(B\) | \(P(A \cap B)\) | \(P(\overline{A} \cap B)\) | \(P(B)\) |
| \(\overline{B}\) | \(P(A \cap \overline{B})\) | \(P(\overline{A} \cap \overline{B})\) | \(P(\overline{B})\) |
| \(P(A)\) | \(P(\overline{A})\) | \(1\) |
Liegt eine Vierfeldertafel der absoluten Häufigkeiten (Anzahlen) vor, lassen sich die bedingten Wahrscheinlichkeiten ebenfalls als Quotient aus dem Eintrag einer inneren Zelle und dem Eintrag einer Randzelle berechnen, denn es gilt beispielsweise:
\[P_{A}(B) = \frac{P(A \cap B)}{P(A)} = \frac{\frac{\vert A \cap B}{\cancel{\vert \Omega \vert}}}{\frac{\vert A \vert}{\cancel{\vert \Omega \vert}}} = \frac{\vert A \cap B \vert}{\vert A \vert }\]
| \(A\) | \(\overline{A}\) | ||
| \(B\) | \(\vert A \cap B \vert\) | \(\vert \overline{A} \cap B \vert\) | \(\vert B \vert\) |
| \(\overline{B}\) | \(\vert A \cap \overline{B} \vert\) | \(\vert \overline{A} \cap \overline{B} \vert\) | \(\vert \overline{B} \vert\) |
| \(\vert A \vert\) | \(\vert \overline{A} \vert\) | \(\vert \Omega \vert\) |
Beispielaufgabe
Ein Unternehmen produziert täglich 10000 integrierte Schaltkreise (Integrated Circuit, IC) eines bestimmten Typs. Erfahrungsgemäß beträgt der Ausschussanteil 1 %. Das eingesetzte elektronisches Verfahren zur Qualitätsprüfung erkennt einen defekten IC mit einer Wahrscheinlichkeit von 99 %. Ein funktionsfähiger IC wird mit 98 % Wahrscheinlichkeit nicht beanstandet.
Betrachtet werden folgende Ereignisse:
\(B\): „Das Prüfverfahren beanstandet den IC."
\(D\): „IC ist defekt."
a) Erstellen Sie eine vollständig ausgefüllte Vierfeldertafel der absoluten Häufigkeiten (Anzahlen).
b) Berechnen Sie die Wahrscheinlichkeiten \(P_{\overline{D}}(B)\) und \(P_{D}(\overline{B})\) und beschreiben Sie deren Bedeutung im Sachzusammenhang.
Ereignisse:
\(B\): „Das Prüfverfahren beanstandet den IC."
\(\overline{B}\): „Das Prüfverfahren beanstandet den IC nicht."
\(D\): „IC ist defekt."
\(\overline{D}\): „IC ist funktionsfähig."
a) Vollständig ausgefüllte Vierfeldertafel der absoluten Häufigkeiten (Anzahlen)
Gegeben:
\[\vert \Omega \vert = 10000\]
\[P(D) = 0{,}01\]
Bedingte Wahrscheinlichkeit: \(P_{D}(B) = 0{,}99\)
Bedingte Wahrscheinlichkeit: \(P_{\overline{D}}(\overline{B}) = 0{,}98\)
Absolute Häufigkeiten (Anzahlen) berechnen:
\[\begin{align*}P(D) = \frac{\vert D \vert}{\vert \Omega \vert} \quad \Longleftrightarrow \quad \vert D \vert &= P(D) \cdot \vert \Omega \vert \\[0.8em] &= 0{,}01 \cdot 10000 \\[0.8em] &= 100\end{align*}\]
\[\vert \overline{D} \vert = \vert \Omega \vert - \vert D \vert = 10000 - 100 = 9900\]
Anhand der gegebenen bedingten Wahrscheinlichkeiten \(P_{D}(B)\) und \(P_{\overline{D}}(\overline{B})\) werden die absoluten Häufigkeiten (Anzahlen) der Ereignisse \(B \cap D\) und \(\overline{B} \cap \overline{D}\) berechnet.
\[\begin{align*} P_{D}(B) &= \frac{P(B \cap D)}{P(D)} \\[0.8em] P_{D}(B) &= \frac{\frac{\vert B \cap D \vert}{\cancel{\vert \Omega \vert}}}{\frac{\vert D \vert}{\cancel{\vert \Omega \vert}}} \\[0.8em] P_{D}(B) &= \frac{\vert B \cap D \vert}{\vert D \vert} \\[0.8em] \Longleftrightarrow \quad \vert B \cap D \vert &= P_{D}(B) \cdot \vert D \vert \\[0.8em] &= 0{,}99 \cdot 100 \\[0.8em] &= 99 \end{align*}\]
\[\begin{align*} P_{\overline{D}}(\overline{B}) &= \frac{P(\overline{B} \cap \overline{D})}{P(\overline{D})} \\[0.8em] P_{\overline{D}}(\overline{B}) &= \frac{\frac{\vert \overline{B} \cap \overline{D} \vert}{\cancel{\vert \Omega \vert}}}{\frac{\vert \overline{D} \vert}{\cancel{\vert \Omega \vert}}} \\[0.8em] P_{\overline{D}}(\overline{B}) &= \frac{\vert \overline{B} \cap \overline{D} \vert}{\vert \overline{D} \vert} \\[0.8em] \Longleftrightarrow \quad \vert \overline{B} \cap \overline{D} \vert &= P_{\overline{D}}(\overline{B}) \cdot \vert \overline{D} \vert \\[0.8em] &= 0{,}98 \cdot 9900 \\[0.8em] &= 9702 \end{align*}\]
Absolute Häufigkeiten in die Vierfeldertafel eintragen:
| \(B\) | \(\overline{B}\) | ||
| \(D\) | \(99\) | \(100\) | |
| \(\overline{D}\) | \(\qquad\) | \(9702\) | \(9900\) |
| \(10000\) |
Vierfeldertafel der absoluten Häufigkeiten (Anzahlen)
Vierfeldertafel zeilen- bzw. spaltenweise durch Subtraktion oder Addition vervollständigen:
\[\begin{align*}\vert \overline{B} \cap D \vert &= \vert D \vert - \vert B \cap D \vert \\[0.8em] &= 100 - 99 \\[0.8em] &= 1\end{align*}\]
\[\begin{align*}\vert B \cap \overline{D} \vert &= \vert \overline{D} \vert - \vert \overline{B} \cap \overline{D} \vert \\[0.8em] &= 9900 - 9702 \\[0.8em] &= 198\end{align*}\]
| \(B\) | \(\overline{B}\) | ||
| \(D\) | \(99\) | \(\textcolor{#e74c3c}{1}\) | \(100\) |
| \(\overline{D}\) | \(\textcolor{#e74c3c}{198}\) | \(9702\) | \(9900\) |
| \(10000\) |
Vierfeldertafel der absoluten Häufigkeiten (Anzahlen)
\[\begin{align*}\vert B \vert &= \vert B \cap D \vert + \vert B \cap \overline{D} \vert \\[0.8em] &= 99 + 198 \\[0.8em] &= 297 \end{align*}\]
\[\begin{align*}\vert \overline{B} \vert &= \vert \overline{B} \cap D \vert + \vert \overline{B} \cap \overline{D} \vert \\[0.8em] &= 1 + 9702 \\[0.8em] &= 9703\end{align*}\]
oder
\[\begin{align*} \vert \overline{B} \vert &= \vert \Omega \vert - \vert B \vert \\[0.8em] &= 10000 - 297 \\[0.8em] &= 9703 \end{align*}\]
| \(B\) | \(\overline{B}\) | ||
| \(D\) | \(99\) | \(\textcolor{#e74c3c}{1}\) | \(100\) |
| \(\overline{D}\) | \(\textcolor{#e74c3c}{198}\) | \(9702\) | \(9900\) |
| \(\textcolor{#e74c3c}{297}\) | \(\textcolor{#e74c3c}{9703}\) | \(10000\) |
Vierfeldertafel der absoluten Häufigkeiten (Anzahlen)
b) Wahrscheinlichkeiten \(P_{\overline{D}}(B)\) und \(P_{D}(\overline{B})\)
Die bedingten Wahrscheinlichkeiten \(P_{\overline{D}}(B)\) und \(P_{D}(\overline{B})\) lassen sich mithilfe der ausgefüllten Vierfeldertafel der absoluten Häufigkeiten berechnen.
| \(B\) | \(\overline{B}\) | ||
| \(D\) | \(99\) | \(1\) | \(100\) |
| \(\overline{D}\) | \(198\) | \(9702\) | \(9900\) |
| \(297\) | \(9703\) | \(10000\) |
Vierfeldertafel der absoluten Häufigkeiten (Anzahlen)
\[\begin{align*}P_{\overline{D}}(B) &= \frac{P(B \cap \overline{D})}{P(\overline{D})} \\[0.8em] &= \frac{\frac{\vert B \cap \overline{D} \vert}{\cancel{\vert \Omega \vert}}}{\frac{\vert \overline{D} \vert}{\cancel{\vert \Omega \vert}}} \\[0.8em] &= \frac{\vert B \cap \overline{D} \vert}{\vert \overline{D} \vert} \\[0.8em] &= \frac{198}{9900} \\[0.8em] &= 0{,}02 \\[0.8em] &= 2\,\% \end{align*}\]
\[\begin{align*}P_{D}(\overline{B}) &= \frac{P(\overline{B} \cap D)}{P(D)} \\[0.8em] &= \frac{\frac{\vert \overline{B} \cap D \vert}{\cancel{\vert \Omega \vert}}}{\frac{\vert D \vert}{\cancel{\vert \Omega \vert}}} \\[0.8em] &= \frac{\vert \overline{B} \cap D \vert}{\vert D \vert} \\[0.8em] &= \frac{1}{100} \\[0.8em] &= 0{,}01 \\[0.8em] &= 1\,\% \end{align*}\]
Bedeutung der bedingten Wahrscheinlichkeiten \(P_{\overline{D}}(B)\) und \(P_{D}(\overline{B})\) im Sachzusammenhang:
\(B\): „Das Prüfverfahren beanstandet den IC."
\(\overline{B}\): „Das Prüfverfahren beanstandet den IC nicht."
\(D\): „IC ist defekt."
\(\overline{D}\): „IC ist funktionsfähig."
Die bedingte Wahrscheinlichkeit \(P_{\overline{D}}(B)\) beschreibt die Wahrscheinlichkeit dafür, dass das Prüfverfahren einen funktionsfähigen IC beanstandet.
Die bedingte Wahrscheinlichkeit \(P_{D}(\overline{B})\) beschreibt die Wahrscheinlichkeit dafür, dass das Prüfverfahren einen defekten IC nicht beanstandet.

