Gegeben ist die Schar der in \(\mathbb R\) definierten Funktionen \(f_{n} \colon x \mapsto x^4 - 2x^n\) mit \(n \in \mathbb N\) sowie die in \(\mathbb R\) definierte Funktion \(f_{0} \colon x \mapsto x^4 - 2\).
Die Abbildungen 1 bis 4 zeigen die Graphen der Funktionen \(f_{0}\), \(f_{1}\), \(f_{2}\) bzw. \(f_{4}\). Ordnen Sie jeder dieser Funktionen den passenden Graphen zu und begründen Sie drei Ihrer Zuordnungen durch Aussagen zur Symmetrie, zu den Schnittpunkten mit den Koordinatenachsen oder dem Verhalten an den Grenzen des Definitionsbereichs des jeweiligen Graphen.
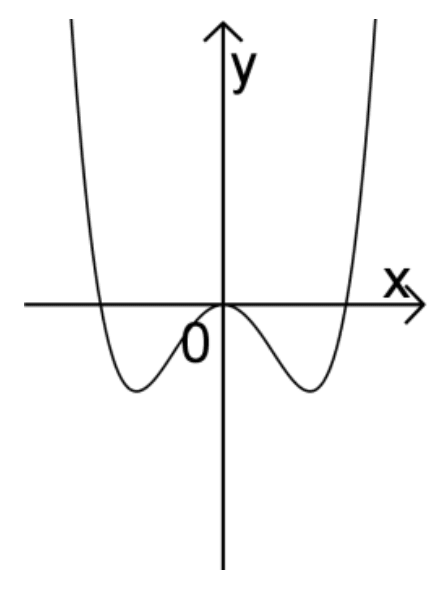 Abb. 1
Abb. 1
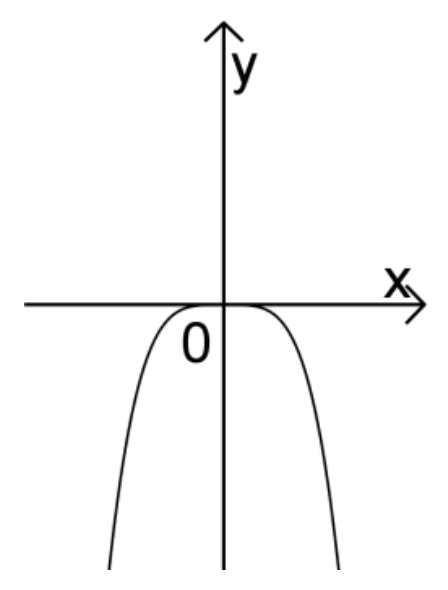 Abb. 2
Abb. 2
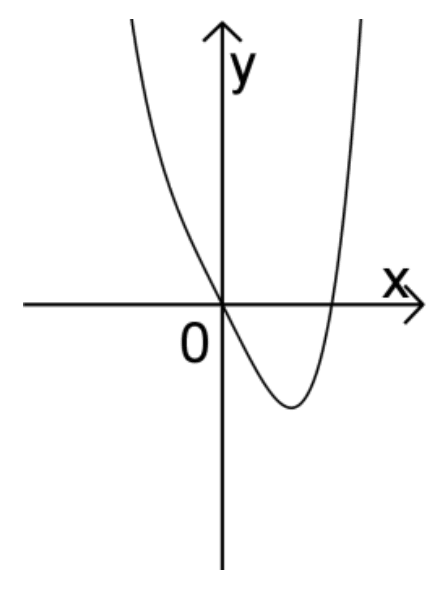 Abb. 3
Abb. 3
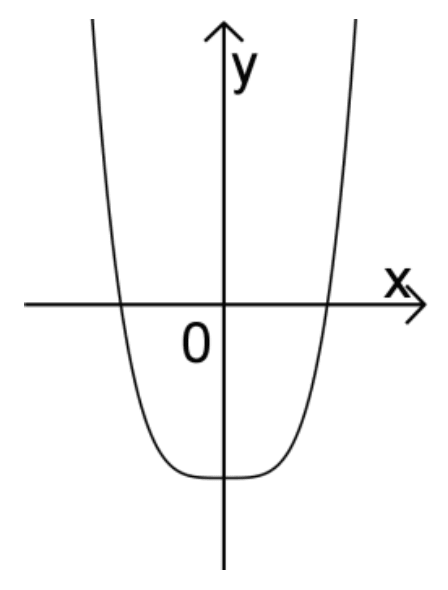 Abb. 4
Abb. 4
(4 BE)
Lösung zu Teilaufgabe 2a
Funktionsgraphen zuordnen
\[f_{n}(x) = x^{4} - 2x^{n}\,; \enspace D = \mathbb R\,, \enspace n \in \mathbb N\]
\[f_{0} = x^{4} - 2\,; \enspace D = R\]
1. Möglichkeit: Funktionsgraphen den Funktionstermen zuordnen
Funktionsterme formulieren:
\[f_{1}(x) = x^{4} -2x = x\cdot (x^{3} - 2)\]
\[f_{2}(x) = x^{4} - 2x^{2} = x^{2} \cdot (x^{2} - 2)\]
\[f_{4}(x) = x^{4} - 2x^{4} = -x^{4}\]
Mögliche Argumentationskette:
Abbildung 4 zeigt einen Funktionsgraphen, der als einziger nicht durch den Ursprung verläuft, sondern die \(y\)-Achse im Negativen schneidet.
\[f_{1}(0) = f_{2}(0) = f_{4}(0) = 0\]
\[f_{0}(0) = -2\,; \enspace S_{y}\,(0|-2)\]
\(\boldsymbol{\Longrightarrow \quad}\) Abb. 4 zeigt den Graphen der Funktion \(\boldsymbol{f_{0}}\).
Von den drei verbleibenden Abbildungen zeigt Abbildung 2 einen Funktionsgraphen, der als einziger eine vierfache Nullstelle im Ursprung besitzt bzw. der als einziger für \(x \to \pm \infty\) gegen \(-\infty\) verläuft.
\[\begin{align*}f_{4}(x) &= 0 \\[0.8em] -x^{4} &= 0 \\[0.8em] x &= 0\end{align*}\]
\(\Longrightarrow \quad x = 0\) ist vierfache Nullstelle des Graphen der Funktion \(f_{4}\).
bzw.
\[\lim \limits_{x \, \to \, \pm \infty} f_{4}(x) = \lim \limits_{x \, \to \, \pm \infty} -x^{4} = -\infty\]
\(\boldsymbol{\Longrightarrow \quad}\) Abb. 2 zeigt den Graphen der Funktion \(\boldsymbol{f_{4}}\).
Von den zwei verbleibenden Abbildungen zeigt Abbildung 1 einen Funktionsgraphen, der als einziger symmetrisch zur \(y\)-Achse verläuft bzw. der als einziger eine doppelte Nullstelle im Ursprung und zwei einfache Nullstellen besitzt.
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
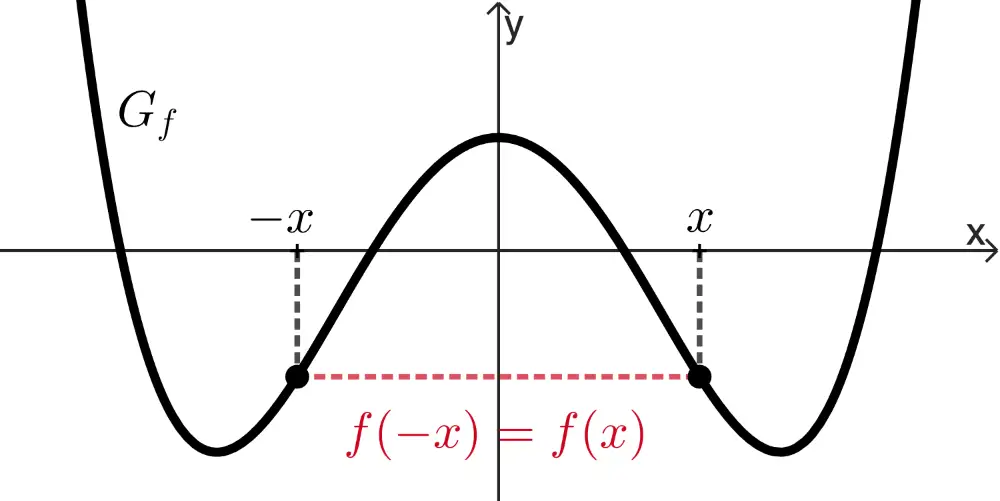
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
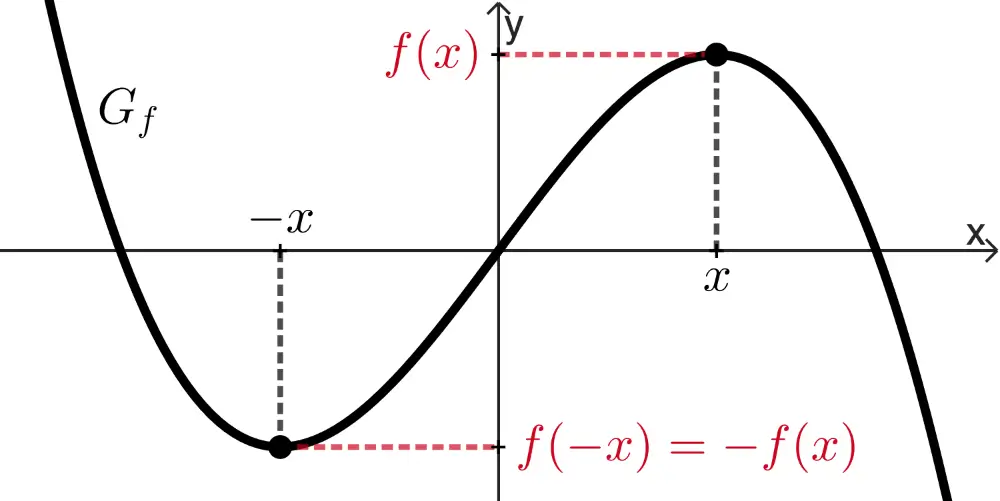
\[f_{2}(-x) = (-x)^{4} - 2 \cdot (-x)^{2} = x^{4} - 2x^{2} = f_{2}(x)\]
\(\Longrightarrow \quad\)Der Graph der Funktion \(f_{2}\) ist achsensymmetrisch zur \(y\)-Achse
Alternative Argunemtation: Der Graph der Funktion \(f_{2}\) ist achsensymmetrisch zur \(y\)-Achse, weil der Funktionsterm der ganzrationalen Funktion \(f_{2}\) ausschließlich aus Potenzen mit geraden Exponenten besteht.
bzw.
\[\begin{align*}f_{2}(x) &= 0 \\[0.8em] x^{2} \cdot (x^{2} - 2) &= 0\end{align*}\]
\(\Longrightarrow \quad x = 0\) ist doppelte Nullstell und \(x = -\sqrt{2}\) sowie \(x = \sqrt{2}\) sind einfache Nullstellen des Graphen der Funktion \(f_{2}\).
\(\boldsymbol{\Longrightarrow \quad}\) Abb. 1 zeigt den Graphen der Funktion \(\boldsymbol{f_{2}}\).
\(\boldsymbol{\Longrightarrow \quad}\) Abb. 3 zeigt den Graphen der Funktion \(\boldsymbol{f_{3}}\) (Ausschlussprinzip).
2. Möglichkeit: Funktionsterme den Funktionsgraphen zuordnen
Funktionsterme formulieren:
\[f_{1}(x) = x^{4} -2x = x\cdot (x^{3} - 2)\]
\[f_{2}(x) = x^{4} - 2x^{2} = x^{2} \cdot (x^{2} - 2)\]
\[f_{4}(x) = x^{4} - 2x^{4} = -x^{4}\]
Mögliche Argumentationskette:
\[f_{4}(x) = -x^{4}\]
Spiegeln von Funktionsgraphen
Spiegelung an der \(x\)-Achse: \(g(x) = -f(x)\)
Spiegelung an der \(y\)-Achse: \(h(x) = f(-x)\)
Der Graph der Funktion \(f_{4}\) geht durch Spiegelung des Graphen der Funktion \(x \mapsto x^{4}\) an der \(x\)-Achse hervor.
Der Wertebereich der Funktion \(f_{4}\) ist \(W = \mathbb R_{0}^{-}\).
\[\lim \limits_{x \, \to \, \pm \infty} -x^{4} = - \infty\]
\(\boldsymbol{\Longrightarrow \quad}\) Abb. 2 zeigt den Graphen der Funktion \(\boldsymbol{f_{4}}\).
\[f_{0}(x) = x^{4} - 2\]
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).

punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)

Der Graph der Funktion \(f_{0}\) ist symmetrisch zur \(y\)-Achse, da der Funktionsterm \(f_{4}(x)\) ausschließlich Potenzen mit geradem Exponenten enthält.
\[f_{0}(-x) = (-x)^{4} - 2 0 x^{4} - 2 = f_{0}(x)\]
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
Der Graph der Funktion \(f_{0}\) geht aus dem Graphen der Funktion \(x \mapsto x^{4}\) durch Verschiebung um -2 in \(y\)-Richtung hervor.
\(\boldsymbol{\Longrightarrow \quad}\) Abb. 4 zeigt den Graphen der Funktion \(\boldsymbol{f_{0}}\).
\[f_{1}(x) = x^{4} - 2x = x \cdot (x^{3} - 2)\]
Der Graph der Funktion \(f_{1}\) besitzt die beiden einfachen Nullstellen \(x = 0\) und \(x = \sqrt[3]{2}\).
Der Graph der ganzrationalen Funktion \(f_{1}\) zeigt kein Symmetrieverhalten, da der Funktionsterm \(f_{1}(x)\) sowohl Potenzen mit geradem als auch ungeradem Exponenten enthält.
\(\boldsymbol{\Longrightarrow \quad}\) Abb. 3 zeigt den Graphen der Funktion \(\boldsymbol{f_{1}}\).
\(\boldsymbol{\Longrightarrow \quad}\) Abb. 1 zeigt den Graphen der Funktion \(\boldsymbol{f_{2}}\) (Ausschlussprinzip).
oder
\[f_{2}(x) = x^{4} - 2x^{2} = x^{2} \cdot (x^{2} - 2)\]
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).

punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)

Der Graph der Funktion \(f_{2}\) ist achsensymmetrisch zur \(y\)-Achse, da der Funktionsterm \(f_{2}(x)\) ausschließlich Potenzen mit geradem Exponenten enthält.
\[f_{2}(-x) = (-x)^{4} - 2 \cdot (-x)^{2} = x^{4} - 2x^{2} = f_{2}(x)\]
Der Graph der Funktion \(f_{2}\) besitzt die beiden einfachen Nullstellen \(x = -\sqrt{2}\) und \(x = \sqrt{2}\) sowie die doppelte Nullstelle \(x = 0\).
\(\boldsymbol{\Longrightarrow \quad}\) Abb. 1 zeigt den Graphen der Funktion \(\boldsymbol{f_{2}}\).
\(\boldsymbol{\Longrightarrow \quad}\) Abb. 3 zeigt den Graphen der Funktion \(\boldsymbol{f_{1}}\) (Ausschlussprinzip).


