Betrachtet wird die Schar der in \(\mathbb R\) definierten Funktionen \(g_k \colon x \mapsto 3x \cdot e^{kx}\) mit \(k \in \mathbb R \backslash \{0\}\). Der Graph jeder Funktion \(g_k\) der Schar hat genau einen Extrempunkt \(E_k\). Abbildung 2 zeigt den Graphen \(G\) einer Funktion dieser Schar.
 Abb. 2
Abb. 2
Alle Extrempunkte \(E_k\) liegen auf der Gerade \(h\). Bestimmen Sie rechnerisch die Steigung von \(h\).
(5 BE)
Lösung zu Teilaufgabe 2a
\[g_k(x) = 3x \cdot e^{kx}; \; D_{g_k} = \mathbb R, \; k \in \mathbb R \backslash \{0\}\]
Vorgehensweise
1. Koordinaten des Extrempunkts \(E_k\) in Abhängigkeit des Parameters \(k\) bestimmen.
2. Für zwei verschiedene Werte von \(k\) die Koordinaten der zugehörigen Extrempunkte berechnen.
3. Mithilfe der Koordinaten der beiden Extrempunkte die Steigung der Gerade \(h\) berechnen.
Koordinaten des Extrempunkts \(\boldsymbol{E_k}\)
Die notwendige Bedingung für eine Extremstelle von \(g_k\) lautet:
Extremstelle(n) bestimmen

Extremstelle(n) bestimmen mit Vorzeichenwechsel der 1. Ableitung
Ist eine Funktion \(f\) in einem Intervall \(I =\, ]a;b[\) differenzierbar und \(x_0\) eine innere Stelle von \(I\), so gilt:
Wenn \(\textcolor{#cc071e}{f'(x_0) = 0}\) ist und \(\textcolor{#cc071e}{f'}\) bei \(x_0\) einen Vorzeichenwechsel
von \(\textcolor{#cc071e}{+}\) nach \(\textcolor{#cc071e}{–}\) hat, dann besitzt \(f\) an der Stelle \(x_0\) ein lokales Maximum \(f(x_0)\).
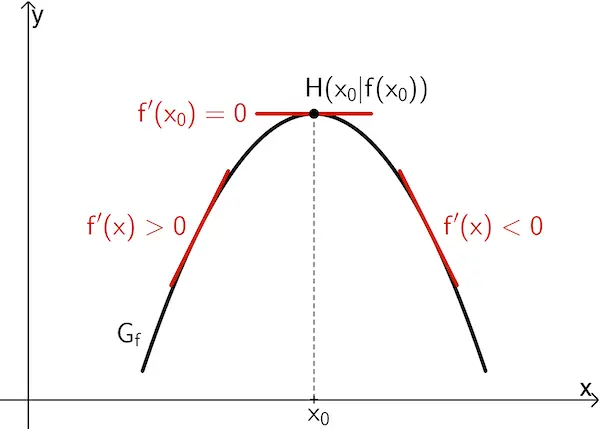
von \(\textcolor{#cc071e}{–}\) nach \(\textcolor{#cc071e}{+}\) hat, dann besitzt \(f\) an der Stelle \(x_0\) ein lokales Minimum \(f(x_0)\).
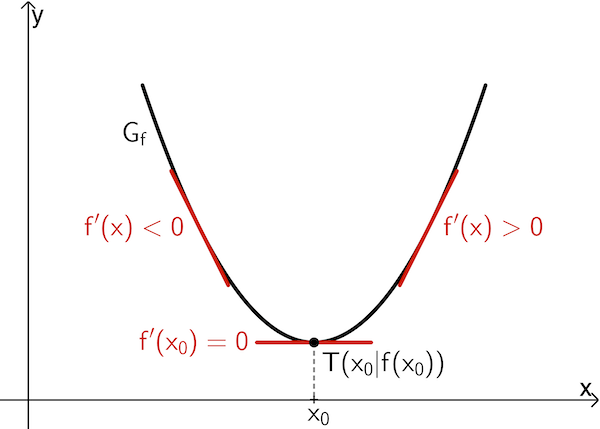
Extremstelle(n) bestimmen mit Vorzeichen der 2. Ableitung
Ist eine Funktion \(f\) in einem Intervall \(I =\, ]a;b[\) zweimal differenzierbar und \(x_0\) eine innere Stelle von \(I\), so gilt:
Wenn \(\textcolor{#e9b509}{f'(x_0) = 0}\) und \(f''(x_0) \textcolor{#cc071e}{\boldsymbol{<}} 0\) ist, dann besitzt \(f\) an der Stelle \(x_0\) ein lokales Maximum \(f(x_0)\).
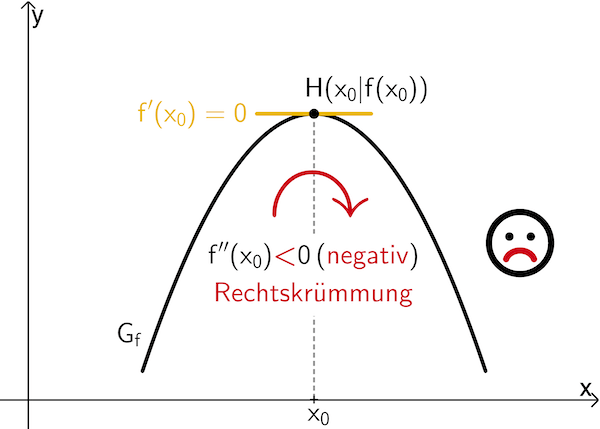
Wenn \(\textcolor{#e9b509}{f'(x_0) = 0}\) und \(f''(x_0) \textcolor{#0087c1}{\boldsymbol{>}} 0\) ist, dann besitzt \(f\) an der Stelle \(x_0\) ein lokales Minimum \(f(x_0)\).
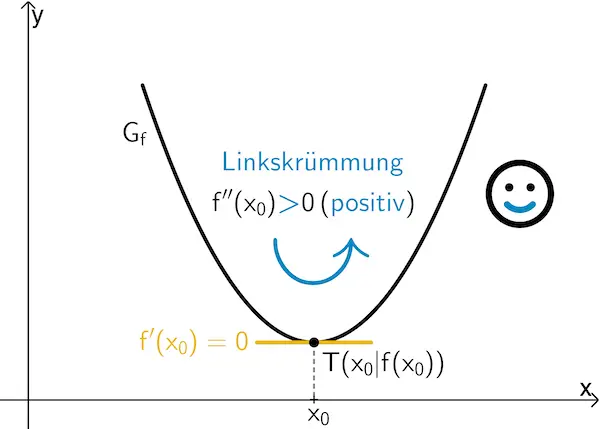
\[g'_k(x) = 0\]
Erste Ableitung \(g'_k\) bilden:
Hierfür wird die Produktregel und die Kettenregel benötigt.
\[g_k(x) = \textcolor{#0087c1}{3x} \cdot \textcolor{#cc071e}{e^{kx}}\]

Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
\[\begin{align*}g'_k(x) &= \underbrace{\textcolor{#0087c1}{3} \cdot \textcolor{#cc071e}{e^{kx}} + \textcolor{#0087c1}{3x} \cdot \overbrace{\textcolor{#cc071e}{e^{kx}} \cdot \textcolor{#cc071e}{k}}^{\text{Kettenregel}}}_{\text{Produktregel}} \\[0.8em] &=\textcolor{#e9b509}{\underset{>\,0}{3e^{kx}}} \cdot (1+kx)\end{align*}\]
\[g'_k(x) = 0 \; \Rightarrow \; 1 + kx = 0 \; \Leftrightarrow \; x = -\frac{1}{k}\]
Für alle \(k \in \mathbb R \backslash \{0\}\) ist \(x = -\dfrac{1}{k}\) eine einfache Nullstelle mit Vorzeichenwechsel von \(g'_k\) und somit eine Extremstelle von \(g_k\).
\(y\)-Koordinate des Extrempunkts \(E_k\):
\[g_k\left(\textstyle{-\frac{1}{k}}\right) = 3 \cdot \left(-\frac{1}{k}\right) \cdot e^{k \cdot \left( -\frac{1}{k}\right)} = -\frac{3}{k} \cdot e^{-1} = -\frac{3}{ke}\]
\[\Rightarrow \; E_k\left( -\frac{1}{k}\bigg| -\frac{3}{ke} \right)\]
Koordinaten von zwei Extrempunkten
Für zwei verschiedene Werte von \(k\), beispielsweise \(k = 1\) und \(k = 3\), ergeben sich die beiden Extrempunkte \(E_1\) und \(E_3\).
\[E_1\left( -1\bigg|-\frac{3}{e}\right)\]
\[E_3\left( -\frac{1}{3}\bigg|-\frac{1}{e}\right)\]
Steigung der Gerade \(\boldsymbol{h}\)
Da alle Extrempunkte \(E_k\) auf der Gerade \(h\) liegen, lässt sich die Steigung \(m\) von \(h\) mithilfe der Koordinaten der Extrempunkte \(E_1\) und \(E_3\) berechnen.
Lineare Funktion
Eine Funktion \(f\) mit \(f(x) = \textcolor{#cc071e}{m}x + \textcolor{#0087c1}{t}\) ist eine lineare Funktion. Dabei ist \(\textcolor{#cc071e}{m}\) die Steigung und \(\textcolor{#0087c1}{t}\) der \(y\)-Achsenabschnitt. Eine lineare Funktion ist eine ganzrationale Funktion vom Grad 1.
Der Graph einer linearen Funktion ist eine Gerade mit der Gleichung \(y = \textcolor{#cc071e}{m}x + \textcolor{#0087c1}{t}\).
Zwei Punkte \(P_1(x_1|y_1)\) und \(P_2(x_2|y_2)\) mit \(x_1 \neq x_2\) legen eine Gerade eindeutig fest. Ebenso ist eine Gerade durch die Angabe der Koordinaten eines Punktes \(P(x_0|y_0)\) sowie der Steigung \(m\) eideutig bestimmt.
Allgemeine Form
\[y = \textcolor{#cc071e}{m}x + \textcolor{#0087c1}{t}\]
Steigung \(\textcolor{#cc071e}{\boldsymbol{m}}\)
\[\textcolor{#cc071e}{m} = \frac{\Delta y}{\Delta x} = \frac{\textcolor{#cc071e}{y_2 - y_1}}{\textcolor{#cc071e}{x_2 - x_1}}\]
parallele Geraden
\[m_1 = m_2\]
Punkt-Steigung-Form
\[y = \textcolor{#cc071e}{m}(x - x_0) + y_0\]
Steigungswinkel \(\textcolor{#cc071e}{\boldsymbol{\alpha}}\)
\[\smash{\textcolor{#cc071e}{m} = \tan{\textcolor{#cc071e}{\alpha}}}\vphantom{\frac{\Delta y}{\Delta x} = \frac{\textcolor{#cc071e}{y_2 - y_1}}{\textcolor{#cc071e}{x_2 - x_1}}}\]
senkrechte Geraden
\[m_1 \cdot m_2 = -1\]

\[\begin{align*}m &= \frac{\Delta y}{\Delta x} = \frac{y_{E_3} - y_{E_1}}{x_{E_3} - x_{E_1}} = \frac{-\frac{1}{e} - \left(-\frac{3}{e}\right)}{-\frac{1}{3} - (-1)} \\[0.8em] &= \frac{\frac{2}{e}}{\frac{2}{3}} = \frac{\cancel{2}}{e} \cdot \frac{3}{\cancel{2}} \\[0.8em] &= \frac{3}{e}\end{align*}\]
Alle Extrempunkte \(E_k\) liegen auf der Gerade \(h\) mit der Steigung \(\frac{3}{e}\).
(Vgl. Mathematik Abiturskript Bayern G9 - 1 Analysis, 1.4.2 Extremstellen einer Funktionenschar, 1.4.6 Ortskurve einer Funktionenschar)


