Der durch das Trapez \(ABCD\) beschriebene Hang wird auf seiner gesamten Fläche für den Weinanbau genutzt. Berechnen Sie den Inhalt der Weinanbaufläche des Hangs in Hektar und untersuchen Sie mithilfe der folgenden Tabelle, um welche Art von Weinanbaulage es sich handelt.

(5 BE)
Lösung zu Teilaufgabe e
Inhalt der Weinanbaufläche des Hangs in Hektar
Hangfläche im Modell: \(A_{ABCD} = \textcolor{#0087c1}{374}\) FE (Flächeneinheiten, vgl. Teilaufgabe b)
Eine Längeneinheit entspricht \(10\,\textsf{m}\) in der Realität (vgl. Angabe).
Somit entspricht eine Flächeneinheit \((10\,\textsf{m})^2 = \textcolor{#e9b509}{100\,\textsf{m}^2}\) in der Realität.
Ein Hektar (ha) misst \(100\,\textsf{m} \cdot 100\,\textsf{m} = \textcolor{#cc071e}{10000\,\textsf{m}^2}\).
Weinanbaufläche in Hektar: \(\dfrac{\textcolor{#0087c1}{374} \cdot \textcolor{#e9b509}{100\,\textsf{m}^2}}{\textcolor{#cc071e}{10000\,\textsf{m}^2}} \textsf{ha} = 3{,}74\,\textsf{ha}\)
Untersuchung der Art der Weinanbaulage

Es ist der Neigungswinkel des Hangs gegenüber der horizontalen Grundfläche zu bestimmen. Dieser entspricht dem Schnittwinkel der Ebene \(H\) (vgl. Teilaufgabe c) und der \(x_1x_2\)-Ebene.

 schematische Darstellung
schematische Darstellung

Schnittwinkel \(\boldsymbol{\varphi}\) zwischen zwei Geraden


\[\begin{align*}\cos{\varphi} &= \frac{\vert \textcolor{#cc071e}{\overrightarrow{u}} \circ \textcolor{#0087c1}{\overrightarrow{v}} \vert}{\vert \textcolor{#cc071e}{\overrightarrow{u}} \vert \cdot \vert \textcolor{#0087c1}{\overrightarrow{v}} \vert} = \cdots \quad(0^{\circ} \leq \varphi \leq 90^{\circ}) \\[0.8em] \varphi &= \cos^{-1}(\cdots)\end{align*}\]
Der Schnittwinkel ist der spitze Winkel \((0^{\circ} < \varphi < 90^{\circ})\), den die Geraden \(\textcolor{#cc071e}{g}\) und \(\textcolor{#0087c1}{h}\) einschließen. Dieser ergibt sich für \(\cos{\varphi} \in \; ]0;1[\). Deshalb wird bei der Schnittwinkelberechnung der Betrag des Skalarprodukts \(\textcolor{#cc071e}{\overrightarrow{u}} \circ \textcolor{#0087c1}{\overrightarrow{v}}\) gewählt.
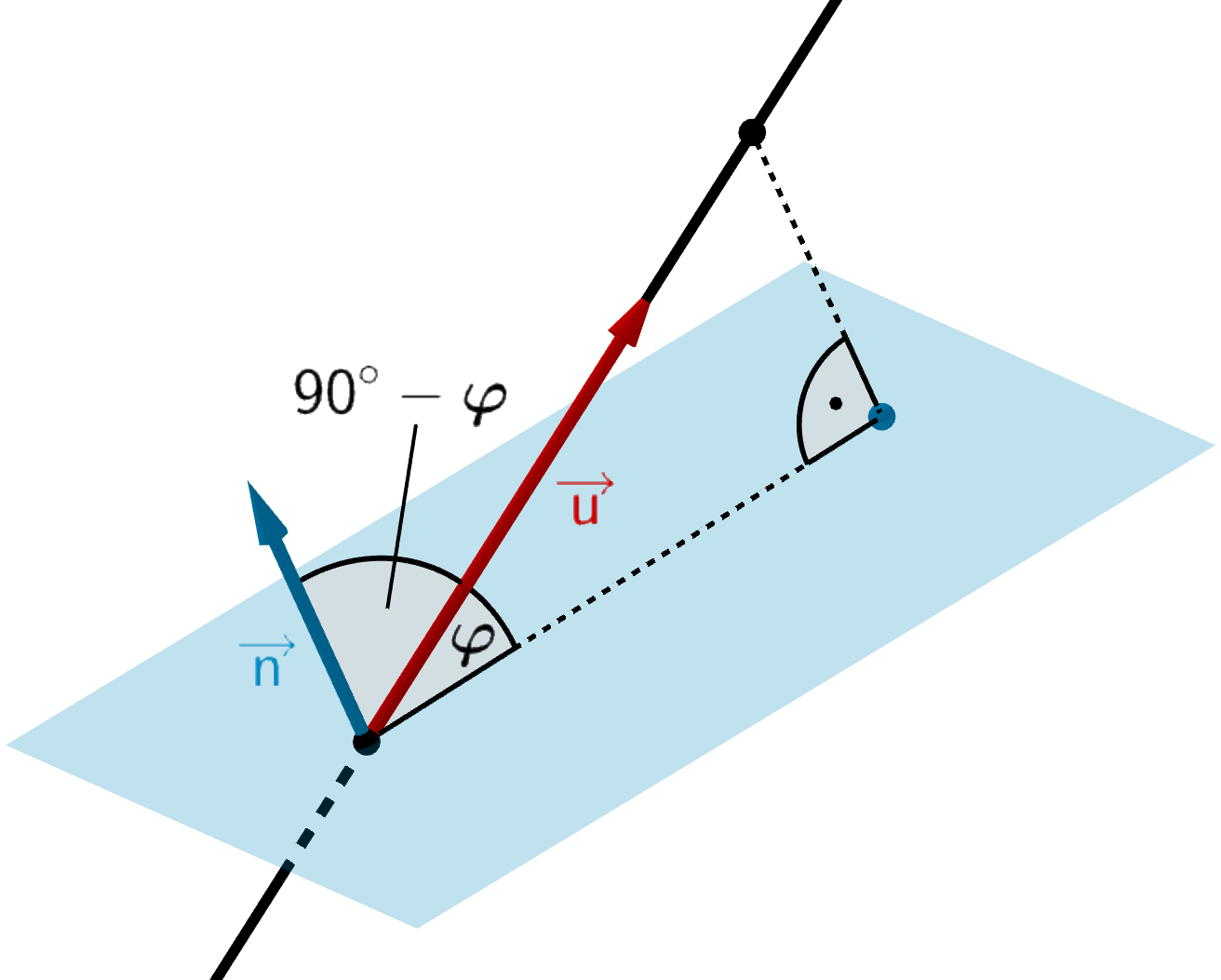
Schnittwinkel \(\boldsymbol{\varphi}\) zwischen Gerade und Ebene
\[\cos{(90^{\circ} - \varphi)} = \frac{\vert \textcolor{#cc071e}{\overrightarrow{u}} \circ \textcolor{#0087c1}{\overrightarrow{n}} \vert}{\vert \textcolor{#cc071e}{\overrightarrow{u}} \vert \cdot \vert \textcolor{#0087c1}{\overrightarrow{n}} \vert}\]
Mit \(\cos{(90^{\circ}-\varphi)} = \sin{\varphi}\) folgt:
\[\begin{align*}\sin{\varphi} &= \frac{\vert \textcolor{#cc071e}{\overrightarrow{u}} \circ \textcolor{#0087c1}{\overrightarrow{n}} \vert}{\vert \textcolor{#cc071e}{\overrightarrow{u}} \vert \cdot \vert \textcolor{#0087c1}{\overrightarrow{n}} \vert} = \cdots \quad(0^{\circ} \leq \varphi \leq 90^{\circ}) \\[0.8em] \varphi &= \sin^{-1}(\cdots)\end{align*}\]
\[\begin{align*}\cos{\varphi} &= \frac{\vert \textcolor{#0087c1}{\overrightarrow{n}_E} \circ \textcolor{#cc071e}{\overrightarrow{n}_F} \vert}{\vert \textcolor{#0087c1}{\overrightarrow{n}_E} \vert \cdot \vert \textcolor{#cc071e}{\overrightarrow{n}_F} \vert} = \cdots \quad(0^{\circ} \leq \varphi \leq 90^{\circ}) \\[0.8em] \varphi &= \cos^{-1}(\cdots)\end{align*}\]

Normalenvektor der Ebene \(\textcolor{#cc071e}{H}\): \(\textcolor{#cc071e}{\overrightarrow{n} = \begin{pmatrix} 8 \\ 0 \\ 15 \end{pmatrix}}\) (vgl. Teilaufgabe c)
Beispielsweise ist \(\textcolor{#0087c1}{\overrightarrow{n}_{x_1x_2} = \begin{pmatrix} 0\\0\\1 \end{pmatrix}}\) ein Normalenvektor der \(\textcolor{#0087c1}{x_1x_2}\)-Ebene.
\[\begin{align*} \cos{\varphi} &= \frac{\vert \textcolor{#cc071e}{\overrightarrow{n}} \circ \textcolor{#0087c1}{\overrightarrow{n}_{x_1x_2}} \vert}{\vert \textcolor{#cc071e}{\overrightarrow{n}} \vert \cdot \vert \textcolor{#0087c1}{\overrightarrow{n}_{x_1x_2}} \vert} = \frac{\left| \textcolor{#cc071e}{\begin{pmatrix} 8 \\ 0 \\ 15 \end{pmatrix}} \circ \textcolor{#0087c1}{\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}} \right|}{\left| \textcolor{#cc071e}{\begin{pmatrix} 8 \\ 0 \\ 15 \end{pmatrix}} \right| \cdot \left| \textcolor{#0087c1}{\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}} \right|} \\[0.8em] &= \frac{\vert \textcolor{#cc071e}{8} \cdot \textcolor{#0087c1}{0} + \textcolor{#cc071e}{0} \cdot \textcolor{#0087c1}{0} + \textcolor{#cc071e}{15} \cdot \textcolor{#0087c1}{1} \vert}{\sqrt{\textcolor{#cc071e}{8}^2 + \textcolor{#cc071e}{0}^2 + \textcolor{#cc071e}{15}^2} \cdot \sqrt{\textcolor{#0087c1}{0}^2 + \textcolor{#0087c1}{0}^2 + \textcolor{#0087c1}{1}^2}} \\[0.8em] &= \frac{15}{17} &&| \; \text{WTR:}\; \cos^{-1}(\dots) \\[2.4em] \varphi &= \cos^{-1}\left( \frac{15}{17} \right) \approx 28{,}1^{\circ} > 17^{\circ}\end{align*}\]
Laut Tabelle handelt es sich bei der Art der Weinanbaulage um eine Steillage.
(Vgl. Mathematik Abiturskript Bayern G9 - 3 Geometrie, 3.6 Schnittwinkelberechnungen)


