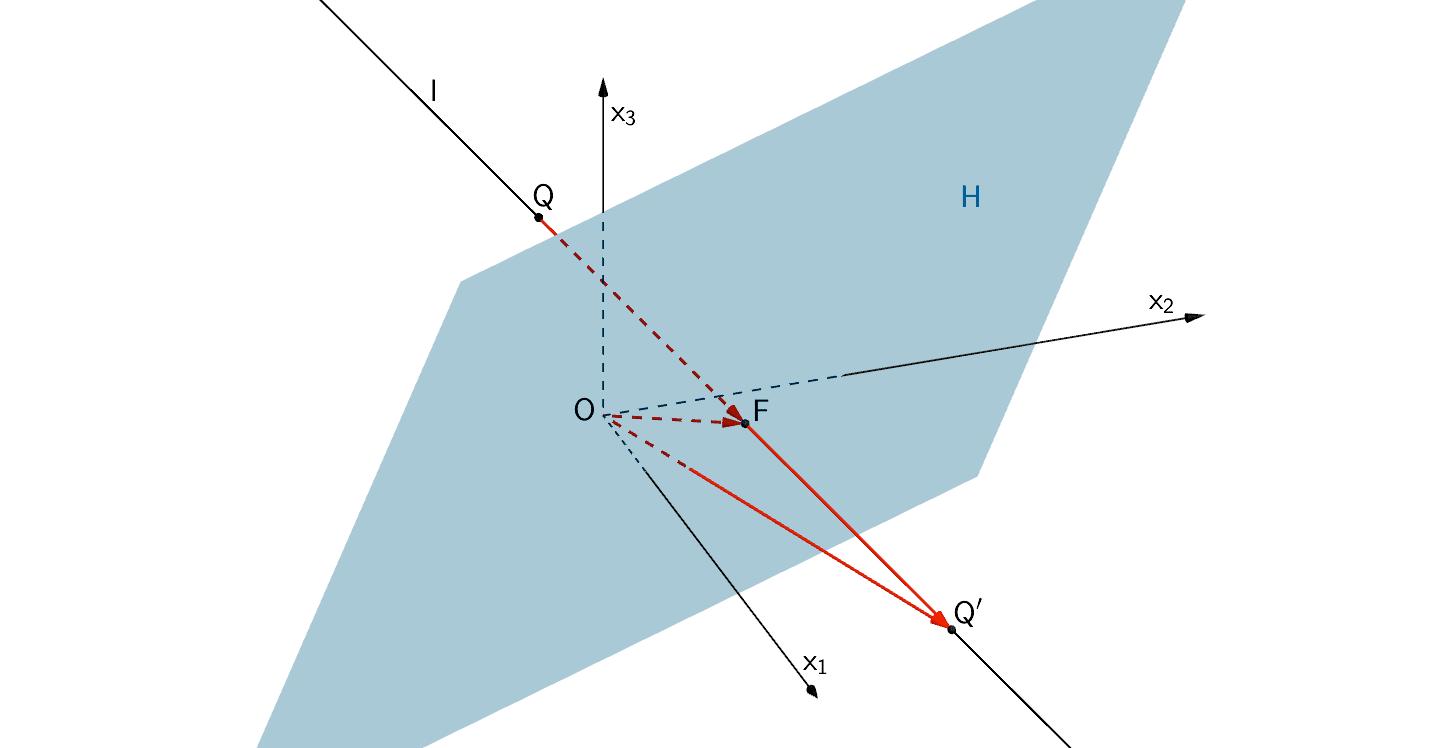
Gegeben sind die Ebene \(H\;\colon\, 2x_1 + x_2 - x_3 = 4\) und der Punkt \(Q\,(-3|0|2)\).
Spiegelt man den Punkt \(Q\) an der Ebene \(H\), so erhält man den Punkt \(Q'\). Ermitteln Sie die Koordinaten von \(Q'\).
(2 BE)
Lösung zu Teilaufgabe 1a
\[H\,\colon\;2x_1 + x_2 - x_3 = 4\,; \qquad Q\,(-3|0|2)\]
Die Lotgerade \(l\) durch den Punkt \(Q\) auf die Ebene \(H\) schneidet die Ebene \(H\) im Lotfußpunkt \(F\).
Es gilt: \(\overrightarrow{Q'} = \overrightarrow{F} + \overrightarrow{FQ'} = \overrightarrow{F} + \overrightarrow{QF}\)
Gleichung der Lotgeradeen \(l\) aufstellen:
Lotgerade auf eine Ebene
\[E\,\colon \overrightarrow{n}_E \circ (\overrightarrow{X} - \overrightarrow{A}) = 0; \quad P\,(p_1|p_2|p_3)\]
Die Lotgerade \(\ell\) mit \(P \in \ell\) auf eine Ebene \(E\) ist durch den Ortsvektor \(\overrightarrow{P}\) und den Normalenvektor \(\overrightarrow{n}_E\) eindeutig bestimmt:
\[\ell\,\colon \overrightarrow{X} = \overrightarrow{P} + \lambda \cdot \overrightarrow{n}_E; \; \lambda \in \mathbb R\]
\[l \perp H\,, \enspace Q \in l \quad \Longrightarrow \quad l\,\colon\;\overrightarrow{X} = \overrightarrow{Q} + \lambda \cdot \overrightarrow{n}_H\,; \enspace \lambda \in \mathbb R\]
\[H\,\colon\;2x_1 + x_2 - x_3 = 4 \quad \Longrightarrow \quad \overrightarrow{n}_H = \begin{pmatrix} 2 \\ 1 \\ -1 \end{pmatrix} \]
\[Q\,(-3|0|2)\]
\[\Longrightarrow \quad l\,\colon\;\overrightarrow{X} = \begin{pmatrix} -3 \\ 0 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ 1 \\ -1 \end{pmatrix}\,; \enspace \lambda \in \mathbb R\]
Koordinaten des Lotfußpunkts \(F\) berechnen:
Der Lotfußpunkt \(F\) ist der Schnittpunkt der Lotgeraden \(l\) mit der Ebene \(H\).
Zur Berechnung des Lotfußpunkts \(F\) setzt man die Koordinaten des Ortsvektors \(\overrightarrow{X}\) aus der Gleichung der Lotgeraden \(l\) in die Normalengleichung der Ebene \(H\) ein und löst die Gleichung nach dem Parameter \(\lambda\) auf. Anschließend setzt man den Parameterwert in die Gleichung der Lotgeraden \(l\) ein und erhält somit die Vektorkoordianten von \(\overrightarrow{F}\).
\[l\,\colon\;\overrightarrow{X} = \begin{pmatrix} -3 \\ 0 \\ 2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ 1 \\ -1 \end{pmatrix}\]
\[H\,\colon\;2x_1 + x_2 - x_3 = 4\]
\[\begin{align*}l \cap H\,\colon\; 2 \cdot (-3 + 2\lambda) + \lambda - (2 - \lambda) &= 4 \\[0.8em] -6 + 4\lambda + \lambda - 2 + \lambda &= 4 \\[0.8em] 6\lambda - 8 &= 4 & &| +8 \\[0.8em] 6\lambda &= 12 & &| :6 \\[0.8em] \lambda &= 2\end{align*}\]
Parametrewert \(\lambda = 2\) in die Gleichung von \(l\) einsetzen:
\[F \in l\,\colon\; \overrightarrow{F} = \begin{pmatrix} -3 \\ 0 \\ 2 \end{pmatrix} + 2 \cdot \begin{pmatrix} 2 \\ 1 \\ -1 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix}\]
Koordinaten des Punktes \(Q'\) berechnen:
\[\overrightarrow{Q'} = \overrightarrow{F} + \overrightarrow{QF}\]
\[\overrightarrow{QF} = \overrightarrow{F} - \overrightarrow{Q} = \begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix} - \begin{pmatrix} -3 \\ 0 \\ 2 \end{pmatrix} = \begin{pmatrix} 4 \\ 2 \\ -2 \end{pmatrix}\]
\[\overrightarrow{Q'} = \begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix} + \begin{pmatrix} 4 \\ 2 \\ -2 \end{pmatrix} = \begin{pmatrix} 5 \\ 4 \\ -2 \end{pmatrix} \quad \Longrightarrow \quad Q'\,(5|4|-2)\]