Geben Sie den Term einer gebrochen-rationalen Funktion \(c\) an, die die beiden folgenden Bedingungen erfüllt:

- Der Graph von \(c\) berührt die \(x\)-Achse an der Stelle \(x = 1\);

- die Funktion \(c\) hat die Polstelle \(x = 3\).

(3 BE)

Lösung zu Teilaufgabe 3

Mögliche gebrochen-rationale Funktion \(c\)

Der Graph von \(c\) berührt die \(x\)-Achse an der Stelle \(x = 1\).

\(\Longrightarrow \quad x = 1\) ist doppelte Nullstelle (ohne Vorzeichenwechsel)

\(\Longrightarrow \quad\) z.B. Zählerterm: \((x -1)^2\)

Die Funktion \(c\) hat die Polstelle \(x = 3\).

\(\Longrightarrow \quad x = 3\) ist Nullstelle des Nenners.

\(\Longrightarrow \quad \) z.B. Nennerterm: \(x - 3\)

\[\Longrightarrow \quad c(x) = \frac {(x - 1)^2}{x - 3}\]

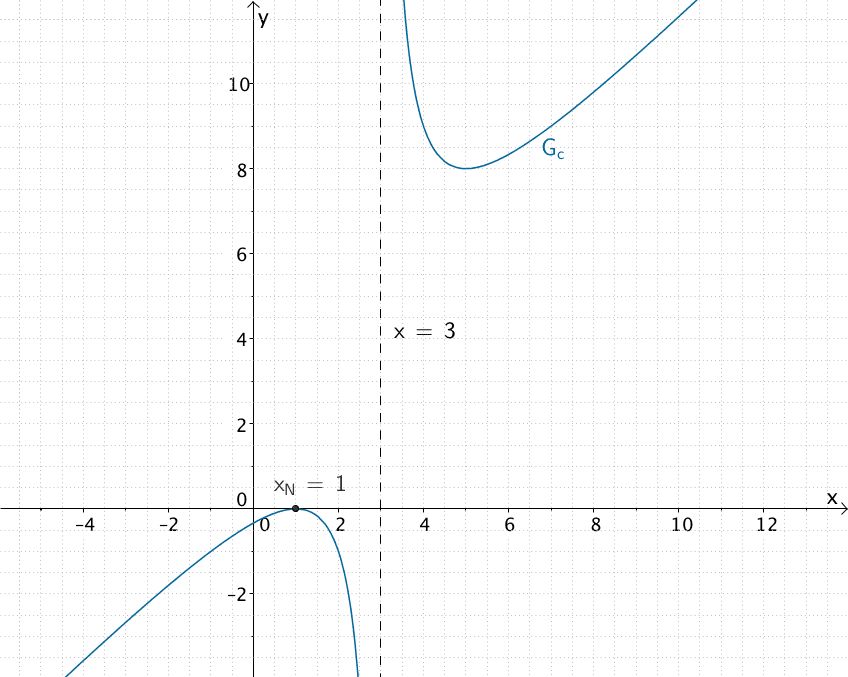
Verlauf des Graphen der gebrochen-rationalen Funktion \(c\)