Ein Pharmaunternehmen führt eine Studie zur Wirksamkeit und Verträglichkeit eines neu entwickelten Medikaments durch. Wenn das Medikament einmalig in Form einer Tablette eingenommen wird, kann die zeitliche Entwicklung der Konzentration des Wirkstoffs im Blut des Patienten modellhaft durch die betrachtete Funktion \(f\) für \(x \in [0;9]\) beschrieben werden. Dabei steht \(x\) für die Zeit in Stunden seit der Einnahme der Tablette und \(f(x)\) für die Konzentration des Wirkstoffs im Blut des Patienten (im Weiteren kurz als Wirkstoffkonzentration bezeichnet) in Milligramm pro Liter \(\big( \frac{\sf{mg}}{\sf{l}}\big)\).
Die folgenden Aufgaben e bis i sollen auf der Grundlage dieses Modells bearbeitet werden.
Berechnen Sie die Wirkstoffkonzentration 30 Minuten nach Einnahme der Tablette und geben Sie die maximal auftretende Wirkstoffkonzentration an.
(2 BE)
Lösung zu Teilaufgabe e
\[f(x) = \frac{4x}{(x + 1)^{2}}; \; x \in [0;9]\]
\(x\): Zeit in Stunden
\(f(x)\): Wirkstoffkonzentration in \(\frac{\sf{mg}}{\sf{l}}\)
Wirkstoffkonzentration 30 Minuten nach Einnahme der Tablette
30 Minuten = 0,5 Stunden, also \(x = 0{,}5\)
\[f(0{,}5) = \frac{4 \cdot 0{,}5}{(0{,}5) + 1}^{2} \approx 0{,}9\]
30 Minuten nach Einnahme der Tablette beträgt die Wirkstoffkonzentration ca, 0,9 \(\frac{\sf{mg}}{\sf{l}}\).
Maximal auftretende Wirkstoffkonzentration
Die maximal auftretende Wirkstoffkonzentration beträgt \(1 \frac{\sf{mg}}{\sf{l}}\).
Begründung (nicht verlangt):
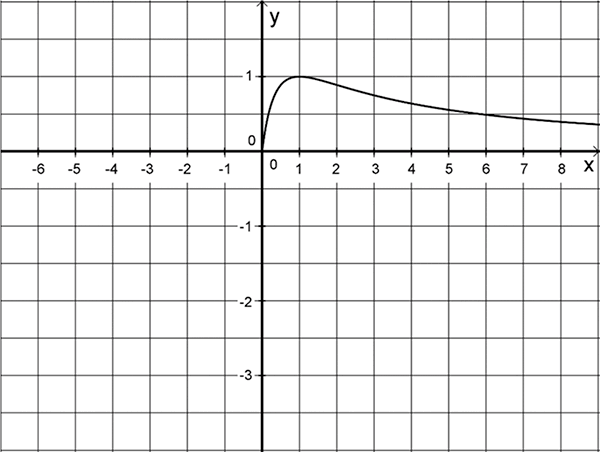
Durch die Abbildung bzw. das Ergebnis aus Teilaufgabe b ist der Hochpunkt \((1|1)\) von \(G_{f}\) bekannt.
Folglich ist die Wirkstoffkonzentration 1 Stunde \((x = 1)\) nach Einnahme der Tablette mit \(1 \frac{\sf{mg}}{\sf{l}}\) \((f(1) = 1)\) maximal.

