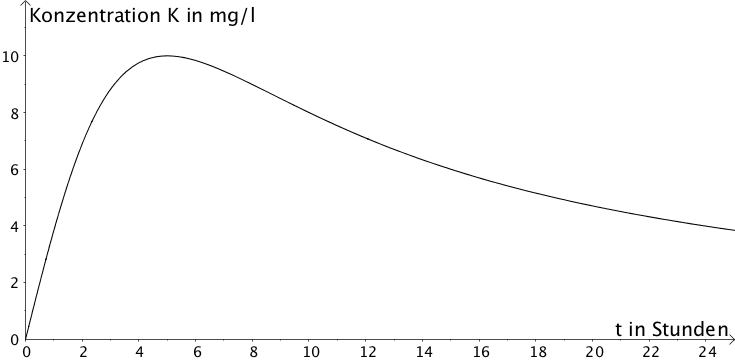
Nach der Einnahme eines Medikaments wird die Konzentration \(K\) des Medikaments im Blut eines Patienten gemessen.
Die Funktion \(K \colon t \mapsto \dfrac{100t}{t^{2} + 25}\) mit \(t \geq 0\) beschreibt näherungsweise den Verlauf \(K(t)\) der Konzentration des Medikaments in Milligramm pro Liter in Abhängigkeit von der Zeit \(t\) in Stunden (vgl. Abbildung).
a) Bestimmen Sie den Zeitpunkt nach der Einnahme des Medikaments, zu dem die Konzentration \(K\) des Medikaments im Blut des Patienten noch 10 % der maximalen Konzentration beträgt auf Minuten genau.
(Teilergebnis: \(K'(t) = -\dfrac{100(t^{2} - 25)}{(t^{2} + 25)^{2}}\))
b) Berechnen Sie die mittlere Änderungsrate der Konzentration \(K\) im Zeitintervall \([10;20]\) und interpretieren Sie das Ergebnis im Sachzusammenhang.
\[K(t) = \frac{100t}{t^{2} + 25}; \; t \geq 0\]
a) Zeitpunkt nach der Einnahme des Medikaments, zu dem die Konzentration \(K\) des Medikaments im Blut des Patienten noch 10 % der maximalen Konzentration beträgt
Zunächst wird die maximale Konzentration \(K_{max}\) nach der Einnahme des Medikaments im Blut des Patienten bestimmt. Anschließend ist die Gleichung \(0{,}1 \cdot K_{max} = K(t)\) zu lösen.
Maximale Konzentration \(K_{max}\) bestimmen:
Zum Zeitpunkt der maximalen Konzentration \(K_{max}\) nimmt die Konzentration des Medikaments im Blut des Patienten weder zu noch ab, das heißt, die momentane Änderungsrate der Konzentration \(K\) ist gleich Null (Einheit: Milligramm pro Liter und Stunde \(\left[\frac{\sf{mg}}{\sf{l} \cdot \sf{h}}\right]\)). Die erste Ableitung \(K'\) beschreibt die momentane Änderungsrate der Konzentration \(K\).
Differentialquotient oder lokale bzw. momentane Änderungsrate
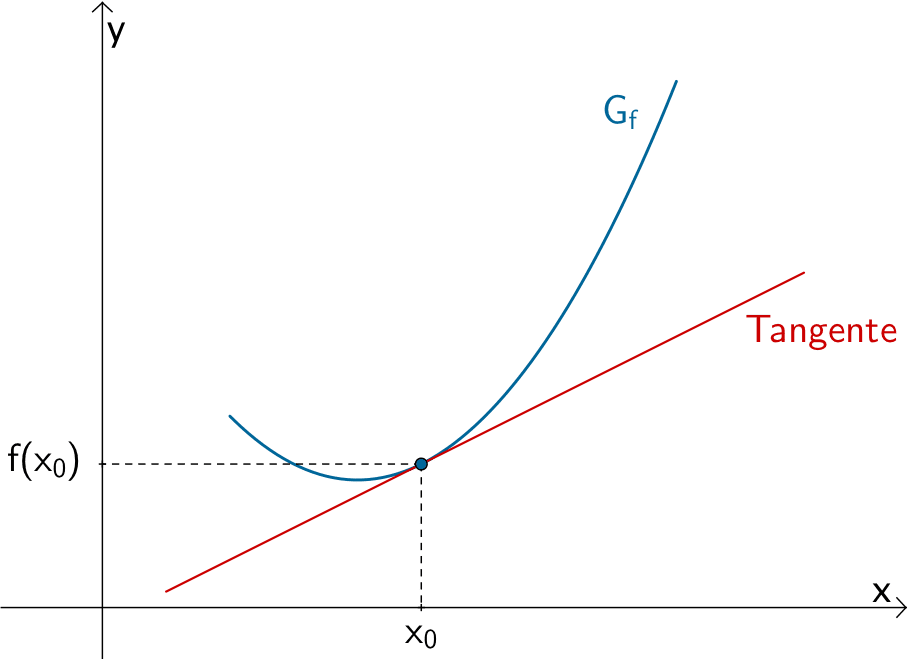
Der Differentialquotient oder die lokale bzw. momentane Änderungsrate \(m_{x_{0}} = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt den Grenzwert des Differenzenquotienten \(\dfrac{f(x) - f(x_{0})}{x - x_{0}}\) bei beliebig genauer Annäherung \(x \to x_{0}\) und damit die Steigung der Tangente an den Graphen der Funktion \(f\) an der Stelle \(x_{0}\).
Man nennt den Grenzwert \(m_{x_{0}}\) die Ableitung von \(f\) an der Stelle \(x_{0}\) und schreibt dafür \(f'(x_{0})\). Voraussetzung: Der Grenzwert existiert an der Stelle \(x_{0}\) und ist endlich.
\[f'(x_{0}) = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\]
(vgl. Merkhilfe)
Folglich lautet die notwendige Bedingung für ein Maximum der Konzentration \(K\):
Anwendung der Differentialrechnung:
Extrempunkte
Ist \(f'(x_{0}) = 0\) und wechselt \(f'\) an der Stelle \(x_{0}\) das Vorzeichen, so hat \(G_{f}\) an der Stelle \(x_{0}\) einen Extrempunkt.
(vgl. Merkhilfe)
\[K'(t) = 0\]
Erste Ableitung \(K'\) bilden:
Die erste Ableitung \(K'\) wird mithilfe der Quotientenregel, der Ableitung einer Potenzfunktion sowie der Summen- und der Faktorregel gebildet.
\[K(t) = \frac{100t}{t^{2} + 25}; \; t \geq 0\]
Quotientenregel
\[f(x) = \frac{u(x)}{v(x)} \quad \Longrightarrow \quad f'(x) = \frac{u'(x) \cdot v(x) - u(x) \cdot v'(x)}{[v(x)]^2}\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
Faktorregel
\(f(x) = a \cdot u(x) \quad \Longrightarrow \quad f'(x) = a \cdot u'(x)\)
Summenregel
\(f(x) = u(x) + v(x) \quad \Longrightarrow \quad f'(x) = u'(x) + v'(x)\)
(vgl. Merkhilfe)
\[\left[ \frac{u(t)}{v(t)} \right]' = \frac{u'(t) \cdot v(t) - u(t) \cdot v'(t)}{\left[ v(t) \right]^{2}}\]
\[u(t) = 100t; \; u'(x) = 100\]
\[v(t) = t^{2} + 25; \, v'(t) = 2t + 0 = 2t\]
\[\begin{align*} K'(t) &= \frac{100 \cdot (t^{2} + 25) - 100t \cdot 2t}{(t^{2} + 25)^{2}} \\[0.8em] &= \frac{100t^{2} + 2500 - 200t^{2}}{(t^{2} + 25)^{2}} \\[0.8em] &= \frac{-100t^{2} + 2500}{(t^{2} + 25)^{2}} \\[0.8em] &= -\frac{100(t^{2} - 25)}{(t^{2} + 25)^{2}} \end{align*}\]
Nullstelle von \(K'\) berechnen:
Ein Bruchterm ist gleich Null, wenn der Zählerterm gleich Null ist.
\[\begin{align*} K'(t) = 0 \quad \Longrightarrow \quad t^{2} - 25 &= 0 & &| + 25 \\[0.8em] t^{2} &= 25 & &| \; \sqrt{\quad} \enspace (t \geq 0) \\[0.8em] t &= 5 \end{align*}\]
Fünf Stunden nach der Einnahme des Medikaments nimmt die Konzentration \(K\) des Medikaments im Blut des Patienten weder zu noch ab, was darauf hinweist, dass die Konzentration \(K\) ein Maximum erreicht hat (vgl. Abbildung).
Nachweis, dass die Konzentration \(K\) zum Zeitpunkt \(t = 5\) maximal ist:
Die Konzentration \(K\) des Medikaments im Blut des Patienten erreicht zum Zeitpunkt \(t = 5\) (Stunden) ein Maximum, wenn die Konzentration für \(t < 5\) zunimmt und für \(t > 5\) abnimmt. Das heißt, wenn die momentane Änderungsrate \(K'(t)\) der Konzentration \(K(t)\) in der Umgebung von \(t = 5\) das Vorzeichen von \(+\) nach \(-\) wechselt.
\[K'(t) = -\frac{100(t^{2} - 25)}{\underbrace{(t^{2} + 25)^{2}}_{>\,0}}\]
Der Zähler von \(K'(t)\) bestimmt den Vorzeichenwechsel von \(K'\) in der Umgebung von \(t = 5\).
\(100(t^{2} - 25) < 0\) für \(t < 5\)
\(100(t^{2} - 25) > 0\) für \(t > 5\)
Somit ergibt sich:
\[\left. \begin{align*} &K'(t) > 0 \; \text{für} \; t < 5 \\[0.8em] &K'(5) = 0 \\[0.8em] &K'(t) < 0 \; \text{für} \; t > 5 \end{align*} \right\} \enspace \Rightarrow \enspace \text{maximale Konzentration}\; K_{max} \; \text{für} \; t = 5\]
Veranschaulichung mit einer Monotonietabelle:
Gemäß dem Monotoniekriterium wird das Monotonieverhalten des Graphen \(G_{K}\) der Funktion \(K(t)\) (vgl. Abbildung Angabe) in der Umgebung von \(t = 5\) betrachtet.
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\[K'(t) = -\frac{100(t - 5)(t + 5)}{\underbrace{(t^{2} + 25)^{2}}_{>\,0}}\]
| \(t\) | \(t < 5\) | \(t = 5\) | \(t > 5\) |
| \(100(t^{2} - 25)\) | \(-\) | \(0\) | \(+\) |
| \(K'(t)\) | \(+\) | \(0\) | \(-\) |
| \(G_{K}\) | \(\nearrow\) | Maximum \((5|K(5))\) | \(\searrow\) |
Maximale Konzentration \(K_{max}\) berechnen:
\[K(t) = \frac{100t}{t^{2} + 25}; \; t \geq 0\]
\[K_{max} = K(5) = \frac{100 \cdot 5}{5^{2} + 25} = \frac{500}{50} = 10\]
Betrachtung möglicher Randextrema:
Bei Extremwertaufgaben ist es grundsätzlich wichtig, mögliche Randextrema zu berücksichtigen, die mit den Mitteln der Differentialrechnung nicht erfasst werden.
Differenzierbarkeit
Existiert für eine Funktion \(f\) an der Stelle \(x_0\) der Differentialquotient
\(\displaystyle f'(x_0) \, = \, \lim \limits_{x\,\to\,x_0} \frac{f(x) - f(x_0)}{x - x_0} \, = \, \lim \limits_{h\,\to\,0} \frac{f(x_0 + h) - f(x_0)}{h}\,\),
heißt die Funktion \(f\) differenzierbar an der Stelle \(\bf{x_0}\).
Der Differentialquotient existiert, wenn der linksseitige Grenzwert des Differentialquotienten (\(\underset{\textcolor{#cc071e}{x\,<\,x_0}}{x\,\to\,x_0}\) bzw. \(\underset{\textcolor{#cc071e}{h\,<\,0}}{h\,\to\,0}\)) und der rechtsseitige Grenzwert des Differentialquotienten (\(\underset{\textcolor{#0087c1}{x\,>\,0}}{x\,\to\,x_0}\) bzw. \(\underset{\textcolor{#0087c1}{h\,>\,0}}{h\,\to\,0}\)) übereinstimmen.
Die Funktion \(K \colon x \mapsto \dfrac{100t}{t^{2} + 25}\) mit \(t \geq 0\) ist für \(t = 0\) nicht differenzierbar, weil der Differentialquotient \(\lim \limits_{x \, \to \, 0} \dfrac{K(t) - K(0)}{t - 0}\) (linksseitig) nicht existiert.
Ein Vergleich von \(K(0)\) mit \(K_{max}\) ergibt:
\[K(0) = 0 \quad \Longrightarrow \quad K(0) < K_{max}\]
Folglich gibt es kein Randmaximum \(K(0)\).
Die Abbildung des zeitlichen Verlaufs \(K(t)\) (vgl. Angabe) sowie der Sachzusammenhang der Aufgabe nehmen diese Erkenntnis vorweg.
Teilergebnis:
Fünf Stunden nach der Einnahme des Medikaments ist die Konzentration des Medikaments im Blut des Patienten mit 10 Milligramm pro Liter maximal.
Zeitpunkt berechnen, zu dem die Konzentration \(K\) noch 10 % der maximalen Konzentration beträgt:
\(K_{max} = 10\) für \(t = 5\)
\[K(t) = \frac{100t}{t^{2} + 25}; \; t \geq 0\]
Die Abgabe „noch 10 % der maximalen Konzentration ..." bedeutet, dass nur Lösungen \(t > 5\) (Stunden) in Frage kommen.
\[\begin{align*} 0{,}1 \cdot K_{max} &= K(t) & & (t > 5) \\[0.8em] 0{,}1 \cdot 10 &= \frac{100t}{t^{2} + 25} \\[0.8em] 1 &= \frac{100t}{t^{2} + 25} & &| \cdot (t^{2} + 25) \\[0.8em] t^{2} + 25 &= 100t & &| - 100t \\[0.8em] t^{2} -100t + 25 &= 0 \end{align*}\]
Die quadratische Gleichung lässt sich mithilfe der Lösungsformel für quadratische Gleichungen lösen.
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[\begin{align*}t_{1,2} &= \frac{100 \pm \sqrt{(-100)^{2} - 4 \cdot 1 \cdot 25}}{2 \cdot 1} \\[0.8em] &= \frac{100 \pm 30\sqrt{11}}{2} \\[0.8em] &= 50 \pm 15\sqrt{11} \qquad (t > 5) \end{align*}\]
\[t_{1} = 50 + \sqrt{11} \approx 99{,}75\]
\[(t_{2} = 50 - \sqrt{11} = 0{,}25)\]
\[0{,}75\;\textsf{h} = 0{,}75 \cdot 60 \; \textsf{min} = 45\; \textsf{min}\]
Ca. 99 Stunden und 45 Minuten nach der Einnahme des Medikaments beträgt die Konzentration des Medikaments im Blut des Patienten noch 10 % der maximalen Konzentration.
b) Mittlere Änderungsrate der Konzentration \(K\) im Zeitintervall \([10;20]\) und Interpretation des Ergebnisses im Sachzusammenhang
Berechnung der mittleren Änderungsrate der Konzentration \(K\) im Zeitintervall \([10;20]\)
Die mittlere Änderungsrate der Konzentration \(K\) im Zeitintervall \([10;20]\) entspricht der Steigung einer Sekante \(S\), welche durch die Punkte \((10|K(10))\) und \((20|K(20))\) des Graphen der Funktion \(K\) verläuft (vgl. Abbildung Angabe). Im Sachzusammenhang ergibt sich die Einheit Milligramm pro Liter und Stunde \(\left[\frac{\sf{mg}}{\sf{l} \cdot \sf{h}}\right]\).
\[K(t) = \frac{100t}{t^{2} + 25}; \; t \geq 0\]
Differenzenquotient oder mittlere Änderungsrate
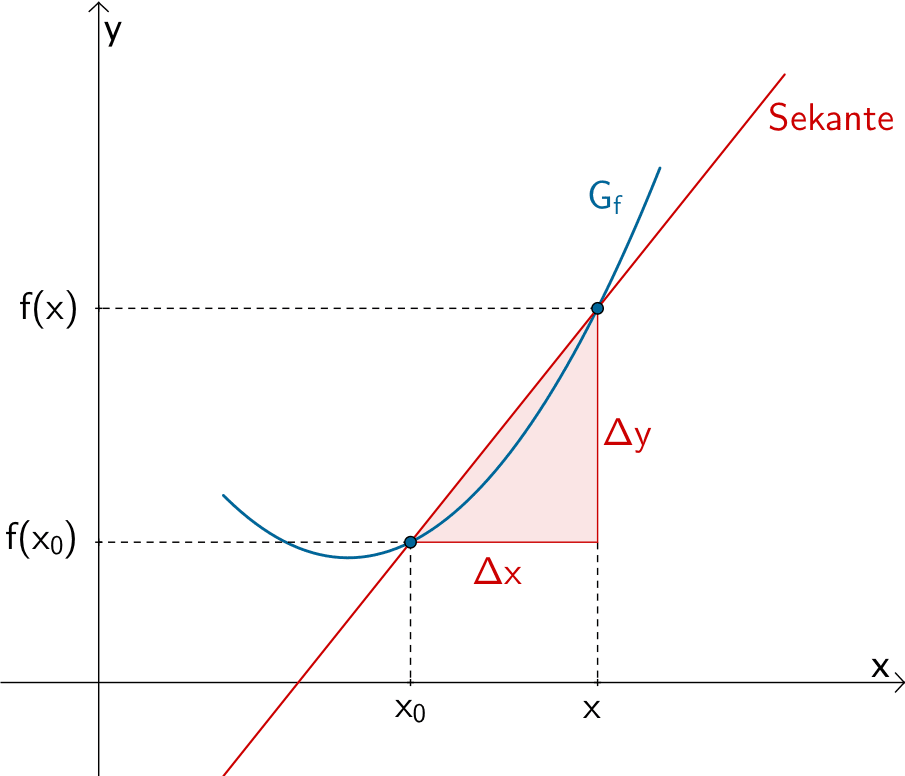
Der Differenzenquotient oder die mittlere Änderungsrate \(m_{s} = \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt die Steigung der Sekante durch den Punkt \((x_{0}|f(x_{0}))\) und einen weiteren Punkt des Graphen der Funktion \(f\).
\[\begin{align*}m_{S} &= \frac{K(20) - K(10)}{20 - 10} \\[0.8em] &= \frac{\frac{100 \cdot 20}{20^{2} + 25} - \frac{100 \cdot 10}{10^{2} + 25}}{10} \\[0.8em] &= -\frac{25}{85} \\[0.8em] &\approx -0{,}33 \end{align*}\]
Im Zeitraum zehn bis zwanzig Stunden nach der Einnahme des Medikaments beträgt die mittlere Änderungsrate der Konzentration \(K\) des Medikaments im Blut des Patienten ca. -0,33 Milligramm pro Liter und Stunde.
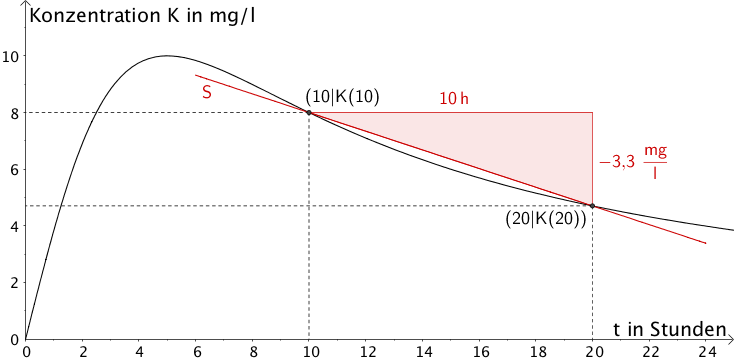
Graphische Veranschaulichung: Die mittlere Änderungsrate der Konzentration \(K\) im Zeitintervall \([10;20]\) entspricht der Steigung der Sekante \(S\) durch die Punkte \((10|K(10))\) und \((20|K(20))\) des Graphen der Funktion \(K \colon x \mapsto \dfrac{100t}{t^{2} + 25}\) mit \(t \geq 0\).
Interpretation des Ergebnisses im Sachzusammenhang
Im Zeitraum zehn bis zwanzig Stunden nach der Einnahme des Medikaments nimmt die Konzentration \(K\) des Medikaments im Blut des Patienten durchschnittlich um ca. 0,33 Milligramm pro Liter und Stunde ab.

