Mathematik Klausur Q12/1-004 Bayern
Aufgabe 1
Berechnen Sie jeweils die Menge aller Stammfunktionen folgender Funktionen:
a) \(f(x) = 2\sqrt{3 - 2x}\)
b) \(g(x) = \ln{\left( x^{2} \right)}; \; x \in \mathbb R^{+}\)
c) \(h(x) = \dfrac{x}{2} \cdot e^{3x^{2} + 4}\)
Aufgabe 2
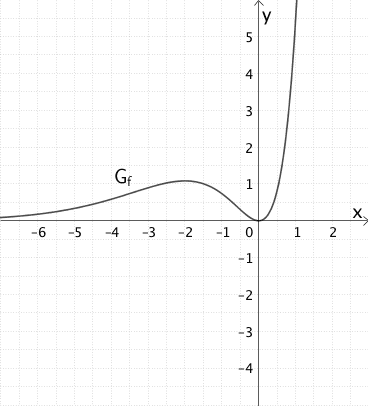
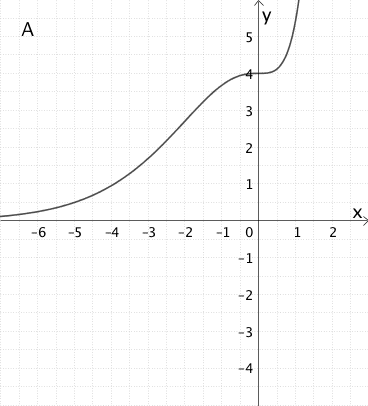
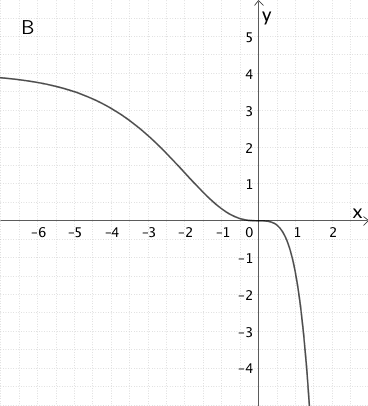
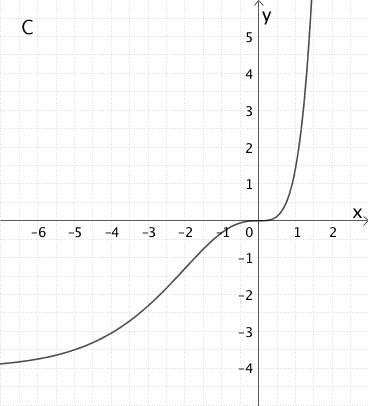
Die Abbildungen zeigen den Graphen \(G_{f}\) einer in \(\mathbb R\) definierten und stetigen Funktion \(f\) sowie die Graphen A, B und C.
Entscheiden Sie, welcher der Graphen A, B oder C den Graphen der Integralfunktion \(\displaystyle I_{0} \colon x \mapsto \int_{0}^{x} f(t) dt\) darstellt, indem Sie begründen weshalb die beiden anderen Graphen nicht in Frage kommen.
Aufgabe 3
Der Graph der Funktion \(f \colon x \mapsto \ln{x}\) und die Normale \(N\) im Punkt \(P(e|f(e))\) schließen im ersten Quadranten mit den Koordinatenachsen ein Flächenstück mit dem Flächeninhalt \(A\) ein.
a) Skizzieren Sie den Graphen \(G_{f}\) der Funktion \(f\) sowie die Normale \(N\) und schraffieren Sie das Flächenstück mit dem Flächeninhalt \(A\).
b) Berechnen Sie den Flächeninhalt \(A\). Rechnen Sie mit exakten Werten.
Aufgabe 4
Ein Unternehmen stellt Tonerkassetten für Laserdrucker her. Eine Tonerkassette vom Typ XL300 kostet in der Herstellung 40 Euro. Aus laufender Qualitätskontrolle ist bekannt, dass 4 % aller Tonerkassetten vom Typ XL300 defekt sind. Im Falle einer defekten Tonerkassette bekommt ein Kunde diese kostenlos ersetzt. Das Unternehmen möchte pro verkaufter Tonerkassette vom Typ XL300 einen Gewinn in Höhe von 10 Euro erzielen.
Zu welchem Preis muss das Unternehmen eine Tonerkassette vom Typ XL300 anbieten?
Aufgabe 5
Ein Laplace-Tetraeder (dreiseitige Pyramide mit vier kongruenten gleichseitigen Dreiecken) ist auf seinen vier Flächen mit je einer der Ziffern 1 bis 4 beschriftet. Es wird folgendes Spiel gespielt:
Ein Spieler zahlt einen Einsatz in Höhe von 1 Euro. Dann setzt er auf eine der Ziffern 1, 2, 3 oder 4 und wirft das Tetraeder anschließend dreimal. Gewertet wird die Ziffer der Fläche, auf der das Tetraeder zu liegen kommt.
Erzielt der Spieler bei keinem Wurf die gesetzte Ziffer, ist der Einsatz verloren.
Erzielt der Spieler einmal die gesetzte Ziffer, erhält er den Einsatz zurück.
Erzielt der Spieler zweimal die gesetzte Ziffer, erhält er den doppelten Einsatz zurück.
Erzielt der Spieler dreimal die gesetzte Ziffer, erhält er den dreifachen Einsatz zurück.
Die Zufallsgröße \(G\) beschreibt den Gewinn eines Spielers pro Spiel in Euro.
a) Ermitteln Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße \(G\).
b) Berechnen Sie den Erwartungswert der Zufallsgröße \(G\) und interpretieren Sie das Ergebnis im Sachzusammenhang.
- Details
- Hauptkategorie: Klausuren Q12/1
Berechnen Sie jeweils die Menge aller Stammfunktionen folgender Funktionen:
a) \(f(x) = 2\sqrt{3 - 2x}\)
b) \(g(x) = \ln{\left( x^{2} \right)}; \; x \in \mathbb R^{+}\)
c) \(h(x) = \dfrac{x}{2} \cdot e^{3x^{2} + 4}\)
- Details
- Hauptkategorie: Klausuren Q12/1
Die Abbildungen zeigen den Graphen \(G_{f}\) einer in \(\mathbb R\) definierten und stetigen Funktion \(f\) sowie die Graphen A, B und C.
Entscheiden Sie, welcher der Graphen A, B oder C den Graphen der Integralfunktion \(\displaystyle I_{0} \colon x \mapsto \int_{0}^{x} f(t) dt\) darstellt, indem Sie begründen weshalb die beiden anderen Graphen nicht in Frage kommen.
- Details
- Hauptkategorie: Klausuren Q12/1
Der Graph der Funktion \(f \colon x \mapsto \ln{x}\) und die Normale \(N\) im Punkt \(P(e|f(e))\) schließen im ersten Quadranten mit den Koordinatenachsen ein Flächenstück mit dem Flächeninhalt \(A\) ein.
a) Skizzieren Sie den Graphen \(G_{f}\) der Funktion \(f\) sowie die Normale \(N\) und schraffieren Sie das Flächenstück mit dem Flächeninhalt \(A\).
b) Berechnen Sie den Flächeninhalt \(A\). Rechnen Sie mit exakten Werten.
- Details
- Hauptkategorie: Klausuren Q12/1
Ein Unternehmen stellt Tonerkassetten für Laserdrucker her. Eine Tonerkassette vom Typ XL300 kostet in der Herstellung 40 Euro. Aus laufender Qualitätskontrolle ist bekannt, dass 4 % aller Tonerkassetten vom Typ XL300 defekt sind. Im Falle einer defekten Tonerkassette bekommt ein Kunde diese kostenlos ersetzt. Das Unternehmen möchte pro verkaufter Tonerkassette vom Typ XL300 einen Gewinn in Höhe von 10 Euro erzielen.
Zu welchem Preis muss das Unternehmen eine Tonerkassette vom Typ XL300 anbieten?
- Details
- Hauptkategorie: Klausuren Q12/1
Ein Laplace-Tetraeder (dreiseitige Pyramide mit vier kongruenten gleichseitigen Dreiecken) ist auf seinen vier Flächen mit je einer der Ziffern 1 bis 4 beschriftet. Es wird folgendes Spiel gespielt:
Ein Spieler zahlt einen Einsatz in Höhe von 1 Euro. Dann setzt er auf eine der Ziffern 1, 2, 3 oder 4 und wirft das Tetraeder anschließend dreimal. Gewertet wird die Ziffer der Fläche, auf der das Tetraeder zu liegen kommt.
Erzielt der Spieler bei keinem Wurf die gesetzte Ziffer, ist der Einsatz verloren.
Erzielt der Spieler einmal die gesetzte Ziffer, erhält er den Einsatz zurück.
Erzielt der Spieler zweimal die gesetzte Ziffer, erhält er den doppelten Einsatz zurück.
Erzielt der Spieler dreimal die gesetzte Ziffer, erhält er den dreifachen Einsatz zurück.
Die Zufallsgröße \(G\) beschreibt den Gewinn eines Spielers pro Spiel in Euro.
a) Ermitteln Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße \(G\).
b) Berechnen Sie den Erwartungswert der Zufallsgröße \(G\) und interpretieren Sie das Ergebnis im Sachzusammenhang.
- Details
- Hauptkategorie: Klausuren Q12/1
2023 Christian Rieger・mathelike
