Ein Teil der Zeltwand, die im Modell durch das Dreieck \(CDS\) dargestellt wird, kann mithilfe zweier vertikal stehender Stangen der Länge 1,80 m zu einem horizontalen Vordach aufgespannt werden (vgl. Abbildung 2). Die dadurch entstehende 1,40 m breite Öffnung in der Zeltwand wird im Modell durch ein Rechteck dargestellt, das symmetrisch zu \(g\) liegt Dabei liegt eine Seite dieses Rechtecks auf der Strecke \([CD]\). Berechnen Sie den Flächeninhalt des Vordachs.
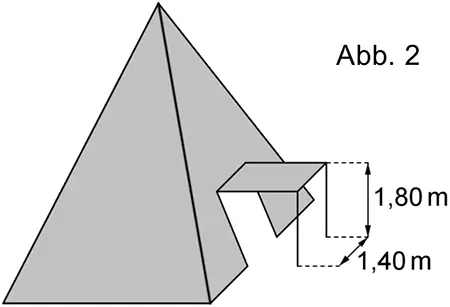
(5 BE)
Lösung zu Teilaufgabe f
Schnittpunkt Gerade - Ebene, Schnittwinkel zweier Ebenen, Trigonometrische Beziehung im rechtwinkligen Dreieck, Flächeninhalt eines Rechtecks
1. Lösungsansatz: Schnittpunkt Symmetrieachse \(g\) - Hilfsebene
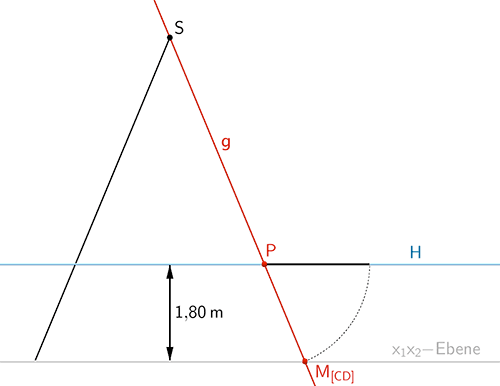
Planskizze: Die Symmetrieachse \(g\) (vgl. Teilaufgabe e) schneidet die Hilfsebene \(H\), in der das horizontale Vordach aufgespannt ist, im Punkt \(P\). Da die Öffnung der Zeltwand (Dreieck \(CDS\)) symmetrisch zu \(g\) liegt, ist die Länge der Strecke \([M_{CD}P]\) gleich der Länge der Öffnung (Länge des Vordachs). Der Punkt \(M_{[CD]}\) ist der Mittelpunkt der Strecke \([CD]\) (vgl. Teilaufgabe e).
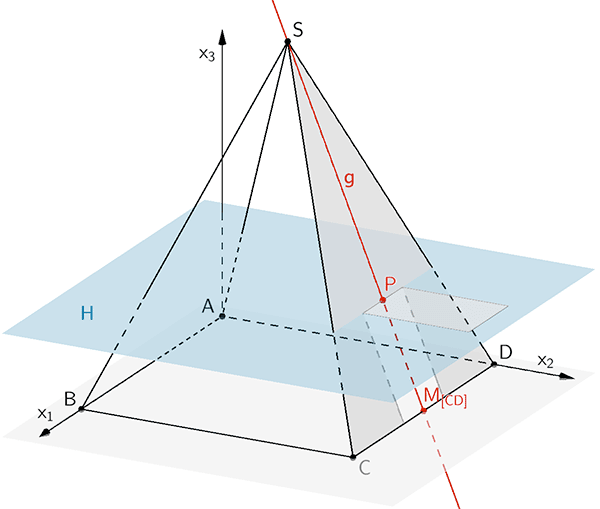
Schnittpunkt \(P\) der Symmetrieachse \(g\) und der Hilfsebene \(H \parallel x_{1}x_{2}\text{-Ebene}\)
Die Breite des Vordachs ist mit 1,40 m bekannt. Eine Längeneinheit entspricht einem Meter (vgl. Angabe, Abbildung 2). Der Flächeninhalt des Vordachs ist gleich dem Flächeninhalt des Rechtecks, das die Öffnung darstellt.
\[\begin{align*} A_{\text{Vordach}} &= A_{\text{Öffnung}} \\[0.8em] &= 1{,}4 \cdot \overline{M_{[CD]}P} \end{align*}\]
Hilfsebene \(H\) aufstellen:
Das horizontale Vordach liegt 1,80 m über der \(x_{1}x_{2}\)-Ebene in der Hilfsebene \(H\):
\[\Longrightarrow \quad H \colon x_{3} = 1{,}8\]
Schnittpunkt \(P\) der Symmetrieachse \(g\) und der Hilfsebene \(H\) berechnen:
Eine Gleichung der Symmetrieachse \(g\) ist aus Teilaufgabe e bekannt.
\[g \colon \overrightarrow{X} = \begin{pmatrix} 2{,}5 \\ 2{,}5 \\ 6 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ -2{,}5 \\ 6 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[H \colon x_{3} = 1{,}8\]
Für die Berechnung des Schnittpunkts \(P\) der Symmetrieachse \(g\) und der Hilfsebene \(H\) wird die \(x_{3}\)-Koordinate des Ortsvektors \(\overrightarrow{X}\) der Gleichung der Symmetrieachse \(g\) in die Gleichung der Hilfseben \(H\) eingesetzt und die Gleichung nach dem Parameter \(\lambda\) aufgelöst.
Der Wert des Parameters \(\lambda\) in die Gleichung der Symmetrieachse \(g\) eingesetzt, ergibt mit \(P \in g\) den Ortsvektor \(\overrightarrow{P}\).
\[\begin{align*} g \cap H \colon 6 + 6\lambda &= 1{,}8 & &| - 6 \\[0.8em] 6\lambda &= -4{,}2 & &| : 6 \\[0.8em] \lambda &= -0{,}7 \end{align*}\]
Parameterwert \(\lambda = -0{,}7\) in \(g\) einsetzen:
\[g \colon \overrightarrow{X} = \begin{pmatrix} 2{,}5 \\ 2{,}5 \\ 6 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ -2{,}5 \\ 6 \end{pmatrix}; \; \lambda \in \mathbb R\]
\[P \in g \colon \overrightarrow{P} = \begin{pmatrix} 2{,}5 \\ 2{,}5 \\ 6 \end{pmatrix} - 0{,}7 \cdot \begin{pmatrix} 0 \\ -2{,}5 \\ 6 \end{pmatrix} = \begin{pmatrix} 2{,}5 \\ 4{,}25 \\ 1{,}8 \end{pmatrix}\]
Länge der Strecke \([M_{[CD]}P]\) berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\(\overrightarrow{P} = \begin{pmatrix} 2{,}5 \\ 4{,}25 \\ 1{,}8 \end{pmatrix}; \; \overrightarrow{M_{[CD]}} = \begin{pmatrix} 2{,}5 \\ 5 \\ 0 \end{pmatrix}\) (vgl. Teilaufgabe e)
\[\begin{align*} \overline{M_{[CD]}P} &= \vert \overrightarrow{M_{[CD]}P} \vert \\[0.8em] &= \vert \overrightarrow{P} - \overrightarrow{M_{[CD]}} \vert \\[0.8em] &= \left| \begin{pmatrix} 2{,}5 \\ 4{,}25 \\ 1{,}8 \end{pmatrix} - \begin{pmatrix} 2{,}5 \\ 5 \\ 0 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 0 \\ -0{,}75 \\ 1{,}8 \end{pmatrix} \right| \\[0.8em] &= \sqrt{0^{2} + (-0{,}75)^{2} + 1{,}8^{2}} \\[0.8em] &= 1{,}95 \end{align*}\]
Die Länge der Öffnung der Zeltwand beträgt 1,95 m.
Flächeninhalt des Vordachs berechnen:
\[\begin{align*} A_{\text{Vordach}} &= 1{,}4 \cdot \overline{M_{[CD]}P} \\[0.8em] &= 1{,}4 \cdot 1{,}95 \\[0.8em] &= 2{,}73 \end{align*}\]
Das Vordach hat einen Flächeninhalt von 2,73 m².
2. Lösungsansatz: Schnittwinkel Ebene \(E\) - \(x_{1}x_{2}\)-Ebene
![Planskizze: Neigungswinkel φ der Ebene E (Dreieck CDS) gegen die x₁x₂-Ebene, Länge [GH] der Öffnung, Lotfußpuinkt F des Lotes des Punktes H auf die x₁x₂-Ebene](/images/stories/B2017_PT_B_G_2/B2017_PT_B_G_2_f_4.png "Planskizze: Neigungswinkel φ der Ebene E (Dreieck CDS) gegen die x₁x₂-Ebene, Länge [GH] der Öffnung, Lotfußpuinkt F des Lotes des Punktes H auf die x₁x₂-Ebene")
Planskizze: Es seien \(G\) und \(H\) zwei Punkte, welche die Länge der Öffnung in der Zeltwand festlegen. Der Punkt \(F\) sei der Lotfußpunkt des Lotes des Punktes \(H\) auf die \(x_{1}x_{2}\)-Ebene. Die Punkte \(F\), \(G\) und \(H\) bilden das rechtwinklige Dreieck \(FGH\). Die Ebene \(E\), in der das Rechteck liegt, das die Öffnung der Zeltwand beschreibt, ist um den Winkel \(\varphi\) gegen die \(x_{1}x_{2}\)-Ebene geneigt.
![Neigungswinkel φ der Ebene E (Dreieck CDS) gegen die x₁x₂-Ebene, Länge [GH] der Öffnung, Lotfußpuinkt F des Lotes des Punktes H auf die x₁x₂-Ebene](/images/stories/B2017_PT_B_G_2/B2017_PT_B_G_2_f_1.png "Neigungswinkel φ der Ebene E (Dreieck CDS) gegen die x₁x₂-Ebene, Länge [GH] der Öffnung, Lotfußpuinkt F des Lotes des Punktes H auf die x₁x₂-Ebene")
Rechtwinkliges Dreieck \(FGH\), Neigungswinkel \(\varphi\) der Ebene \(E\) gegen die \(x_{1}x_{2}\)-Ebene
Die Breite des Vordachs ist mit 1,40 m bekannt. Eine Längeneinheit entspricht einem Meter (vgl. Angabe, Abbildung 2). Der Flächeninhalt des Vordachs ist gleich dem Flächeninhalt des Rechtecks, das die Öffnung darstellt.
\[\begin{align*} A_{\text{Vordach}} &= A_{\text{Öffnung}} \\[0.8em] &= 1{,}4 \cdot \overline{GH} \end{align*}\]
Länge der Strecke \([GH]\) beschreiben:
Die Länge der Strecke \([GH]\) lässt sich mithilfe einer trigonometrischen Beziehung im rechtwinkligen Dreieck \(FGH\) formulieren. Die Länge der Strecke \([FH]\) entspricht der Länge der vertikalen Stangen, die das Vordach horizontal aufspannen (vgl. Angabe, Abbildung 2). Das heißt, es gilt: \(\overline{FG} = 1{,}8\).
Trigonometrische Beziehungen im rechtwinkligen Dreieck (vgl. Merkhilfe)
\[\sin \alpha = \frac{\text{Gegenkathete}}{\text{Hypotenuse}}\]
\[\cos \alpha = \frac{\text{Ankathete}}{\text{Hypotenuse}}\]
\[\tan \alpha = \frac{\text{Gegenkathete}}{\text{Ankathete}}\]
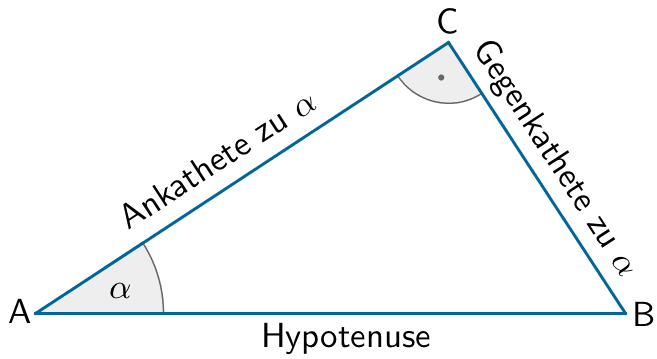
\[\sin{\varphi} = \frac{\overline{FH}}{\overline{GH}} \quad \Longleftrightarrow \quad \overline{GH} = \frac{\overline{FH}}{\sin{\varphi}}\]
Neigungswinkel \(\varphi\) der Ebene \(E\) gegen die \(x_{1}x_{2}\)-Ebene bestimmen:
De Neigungswinkel \(\varphi\) der Ebene \(E\) gegen die \(x_{1}x_{2}\)-Ebene entspricht dem Schnittwinkel der beiden Ebenen. Dieser Winkel ist gleich dem spitzen Winkel, den ein Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) und eine Normalenvektor \(\overrightarrow{n}_{x_{1}x_{2}}\) der \(x_{1}x_{2}\)-Ebene einschließen.
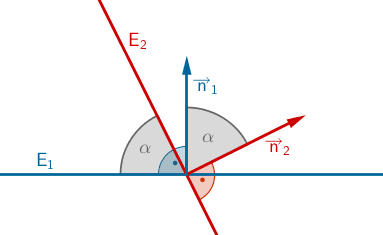
Schnittwinkel \(\boldsymbol{\alpha}\) zweier Ebenen
\[E_1\colon \enspace \overrightarrow{n}_1 \circ \left( \overrightarrow{X} - \overrightarrow{A} \right) = 0\]
\[E_2\colon \enspace \overrightarrow{n}_2 \circ \left( \overrightarrow{X} - \overrightarrow{B} \right) = 0\]
\[\cos \alpha = \frac{\vert \overrightarrow{n}_1 \circ \overrightarrow{n}_2 \vert}{\vert \overrightarrow{n}_1 \vert \cdot \vert \overrightarrow{n}_2 \vert} \enspace \Rightarrow \enspace \alpha = \cos^{-1}(\dots)\]
\[(0^{\circ} \leq \alpha \leq 90^{\circ})\]
Ein Normalenvektor der Ebene \(E\) ergibt sich aus der Gleichung der Ebene \(E\) in Normalenform in Koodinatendarstellung (vgl. Angabe).
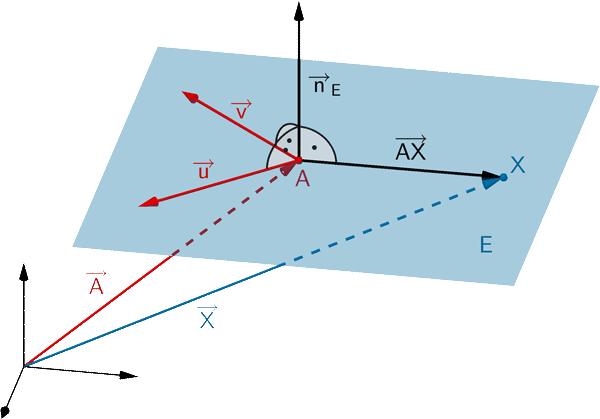
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jede Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\[E \colon 12x_{2} + 5x_{3} = 60 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 0 \\ 12 \\ 5 \end{pmatrix}\]
Ein Normalenvektor der \(x_{1}x_{2}\)-Ebene ist beispielsweise \(\overrightarrow{n}_{x_{1}x_{2}} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\).
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \cos \varphi &= \frac{\left| \overrightarrow{n}_{E} \circ \overrightarrow{n}_{x_{1}x_{2}} \right|}{\left| \overrightarrow{n}_{E} \right| \cdot \left| \overrightarrow{n}_{x_{1}x_{2}} \right|} \\[0.8em] &= \frac{\left| \begin{pmatrix} 0 \\ 12 \\ 5 \end{pmatrix} \circ \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right|}{\left| \begin{pmatrix} 0 \\ 12 \\ 5 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right|} \\[0.8em] &= \frac{\vert 0 \cdot 0 + 12 \cdot 0 + 5 \cdot 1 \vert}{\sqrt{0^{2} + {12}^{2} + 5^{2}} \cdot \sqrt{0^{2} + 0^{2} + 1^{2}}} \\[0.8em] &= \frac{5}{13} & &| \; \text{TR:} \; \cos^{-1}(\dots) \\[3.2em] \varphi &\approx 67{,}38^{\circ}\end{align*}\]
Länge der Strecke \([GH]\) berechnen:
\(\overline{FH} = 1{,}8\) (vgl. oben)
\[\begin{align*}\overline{GH} &= \frac{\overline{FH}}{\sin{\varphi}} \\[0.8em] &= \frac{1{,}8}{\sin{67{,}38^{\circ}}} \\[0.8em] &\approx 1{,}95 \end{align*}\]
Die Länge der Öffnung der Zeltwand beträgt 1,95 m.
Flächeninhalt des Vordachs berechnen:
\[\begin{align*} A_{\text{Vordach}} &= 1{,}4 \cdot \overline{GH} \\[0.8em] &= 1{,}4 \cdot 1{,}95 \\[0.8em] &= 2{,}73 \end{align*}\]
Das Vordach hat einen Flächeninhalt von 2,73 m².
