Gegeben ist die Funktion \(f\) mit \(f(x) = -\dfrac{3}{x - 2}\).
a) Bestimmen Sie \(\lim \limits_{x\,\to\,-\infty}f(x)\) und \(\lim \limits_{x\,\to\,+\infty}f(x)\). Beschreiben Sie Ihre Ergebnisse in Worten und interpretieren Sie diese graphisch.
b) Der Graph der Funktion \(g\) geht aus dem Graphen der Funktion \(f\) durch Verschiebung in \(x\)-Richtung und in \(y\)-Richtung hervor, wobei er die Asymptoten mit den Gleichungen \(x = 3\) und \(y = -2\) besitzt. Geben Sie die zugehörige Verschiebung in \(x\)-Richtung und in \(y\)-Richtung an sowie einen Funktionsterm von \(g\).
c) Der Graph der Funktion \(h\) entsteht aus dem Graphen der Funktion \(f\) durch eine Streckung mit dem Faktor \(3\) in \(y\)-Richtung und eine anschließende Verschiebung um \(2\) in \(y\)-Richtung. Der Graph der Funktion \(k\) entsteht aus dem Graphen der Funktion \(f\) durch die angegebene Streckung und Verschiebung in umgekehrter Reihenfolge. Entscheiden Sie, ob folgende Aussage richtig ist: „Die Funktionsterme von \(h\) und \(k\) unterscheiden sich." Begründen Sie ihre Entscheidung.
a) Grenzwerte \(\lim \limits_{x\,\to\,-\infty}f(x)\) und \(\lim \limits_{x\,\to\,+\infty}f(x)\) bestimmen, beschreiben und graphisch interpretieren
\[f(x) = -\frac{3}{x-2}\]
Bestimmung der Grenzwerte
\[\lim \limits_{x\,\to\,-\infty}f(x) = \lim \limits_{x\,\to\,-\infty} -\frac{3}{\textcolor{#e9b509}{\underbrace{x - 2}_{\to\,-\infty}}} = 0^{\textcolor{#0087c1}{\boldsymbol{+}}}\]
\[\lim \limits_{x\,\to\,+\infty}f(x) = \lim \limits_{x\,\to\,+\infty} -\frac{3}{\textcolor{#e9b509}{\underbrace{x - 2}_{\to\,+\infty}}} = 0^{\textcolor{#cc071e}{\boldsymbol{–}}}\]
Beschreibung der Grenzwerte in Worten
Die Funktion \(f\) konvergiert für \(x \to -\infty\) gegen den Grenzwert \(0\), wobei die Funktionswerte positiv sind.
Die Funktion \(f\) konvergiert für \(x \to +\infty\) gegen den Grenzwert \(0\), wobei die Funktionswerte negativ sind.
Graphische Interpretation der Grenzwerte
Die Grenzwertbetrachtung zeigt, das der Graph der gebrochrationalen Funktion \(f\) für \(x \to -\infty\) bzw. \(x \to +\infty\) die waagrechte Asymptote mit der Gleichung \(y = 0\) besitzt, also die \(x\)-Achse.
Für \(x \to -\infty\) nähert sich der Graph der Funktion \(f\) von oben (aus dem Positiven) der \(x\)-Achse an.
Für \(x \to +\infty\) nähert sich der Graph der Funktion \(f\) von unten (aus dem Negativen) der \(x\)-Achse an.
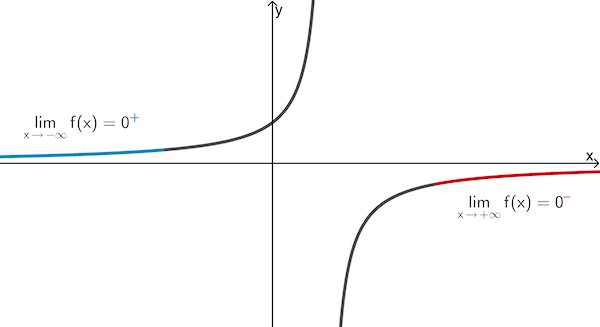 (Skizze nicht verlangt)
(Skizze nicht verlangt)
b) Verschiebungen in \(x\)- und \(y\)-Richtung sowie einen Funktionsterm von \(g\) angeben
\[f(x) = -\frac{3}{x-2}\]
Verschiebung in \(\boldsymbol{x}\)-Richtung
Die Funktion \(f\) hat an der Nennernullstelle \(x = 2\) eine Definitionslücke. Die einfache Nennernullstelle \(x = 2\) ist Polstelle (mit Vorzeichenwechsel). Der Graph von \(f\) besitzt somit die senkrechte Asymptote mit der Gleichung \(x = 2\).
Der Graph von \(g\) besitzt die senkrechte Asymptote mit der Gleichung \(x = 3\) (vgl. Angabe).
Folglich ist der Graph von \(g\) bezüglich des Graphen von \(f\) um \(\boldsymbol{1}\) in \(\boldsymbol{x}\)-Richtung verschoben.
Verschiebung in \(\boldsymbol{y}\)-Richtung
Der Graph der Funktion \(f\) besitzt die \(x\)-Achse mit der Gleichung \(y = 0\) als waagrechte Asymptote (vgl. Teilaufgabe 1a).
Der Graph der Funktion \(g\) besitzt die waagrechte Asymptote mit der Gleichung \(y = -2\) (vgl. Angabe).
Folglich ist der Graph der Funktion \(g\) bezüglich des Graphen der Funktion \(f\) um \(\boldsymbol{-2}\) in \(\boldsymbol{y}\)-Richtung verschoben.
Funktionsterm von \(\boldsymbol{g}\)
Aufgrund der Verschiebung des Graphen von \(g\) bezüglich des Graphen von \(f\) um \(\textcolor{#0087c1}{1}\) in \(\textcolor{#0087c1}{x}\)-Richtung und \(\textcolor{#cc071e}{-2}\) in \(\textcolor{#cc071e}{y}\)-Richtung folgt:
Verschieben von Funktionsgraphen
\(g(x) = f(x +c) + d\) mit \(c,d \in \mathbb R\)
Verschieben um \(-c\) in \(x\)-Richtung
Verschieben um \(d\) in \(y\)-Richtung
\[g(x) = f(\textcolor{#0087c1}{x - 1}) \textcolor{#cc071e}{- 2}\]
oder
\[g(x) = -\frac{3}{(\textcolor{#0087c1}{x - 1}) - 2} \textcolor{#cc071e}{- 2} = -\frac{3}{x - 3} - 2\]
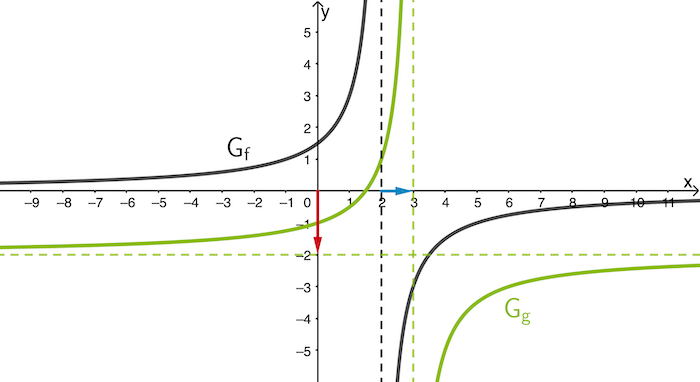 (Skizze nicht verlangt)
(Skizze nicht verlangt)
c) Aussage „Die Funktionsterme von \(h\) und \(k\) unterscheiden sich." beurteilen
Die Aussage ist richtig.
Die Begründung erfolgt durch einen Vergleich der Funktionsterme von \(h\) und \(k\).
Betrachtung der Funktion \(\boldsymbol{h}\)
„Der Graph der Funktion \(h\) entsteht aus dem Graphen der Funktion \(f\) durch eine Streckung mit dem Faktor \(\textcolor{#0087c1}{3}\) in \(\textcolor{#0087c1}{y}\)-Richtung und eine anschließende Verschiebung um \(\textcolor{#cc071e}{2}\) in \(\textcolor{#cc071e}{y}\)-Richtung."
Strecken von Funktionsgraphen
Strecken mit dem Faktor \(a\) in \(y\)-Richtung
\(g(x) = a \cdot f(x)\) mit \(a \in \mathbb R^+\)
Strecken mit dem Faktor \(\dfrac{1}{b}\) in \(x\)-Richtung
\(h(x) = f(b \cdot x)\) mit \(b \in \mathbb R^+\)
\[h(x) = \textcolor{#0087c1}{3} \cdot f(x) + \textcolor{#cc071e}{2}\]
Verschieben von Funktionsgraphen
\(g(x) = f(x +c) + d\) mit \(c,d \in \mathbb R\)
Verschieben um \(-c\) in \(x\)-Richtung
Verschieben um \(d\) in \(y\)-Richtung
Betrachtung der Funktion \(\boldsymbol{k}\)
Der Graph der Funktion \(k\) entsteht aus dem Graphen der Funktion \(f\) durch die angegebene Streckung und Verschiebung in umgekehrter Reihenfolge.
\[k(x) = \textcolor{#0087c1}{3} \cdot (f(x) + \textcolor{#cc071e}{2}) = 3 \cdot f(x) + 6 = h(x) + \textcolor{#e9b509}{4}\]
Vergleich
Die Funktionsterme von \(h\) und \(k\) unterscheiden sich durch die additive Konstante \(\textcolor{#e9b509}{4}\).


