Aufgabe 1
Geben Sie von folgenden Funktionen jeweils die maximale Definitionsmenge an und bestimmen Sie jeweils die Nullstelle(n). Bilden Sie jeweils die Ableitungsfunktion und vereinfachen Sie soweit wie möglich.
a) \(f(x) = 2\ln{(3\sqrt{x})}\)
b) \(g(x) = xe^{4 - 3x} + \dfrac{x^{2}}{e^{3x - 4}}\)
c) \(h(x) = x^{3} \cdot \sin{\left( \dfrac{\pi}{3}x \right)}\)
Aufgabe 2
Gegeben ist die Funktion \(f \colon x \mapsto \ln{\left( -\dfrac{3}{x} \right)}\). Der Graph der Funktion \(f\) wird mit \(G_{f}\) bezeichnet.
a) Bestimmen Sie das Verhalten von \(f\) an den Rändern des Definitionsbereichs \(D_{f}\).
b) Zeigen Sie durch Rechnung, dass \(G_{f}\) in \(D_{f}\) linksgekrümmt ist.
Aufgabe 3
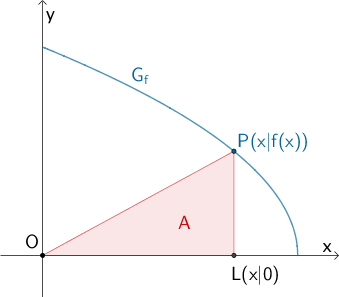
Die Abbildung zeigt den Graphen \(G_{f}\) der Funktion \(f \colon x \mapsto 2\sqrt{6 - x}\) mit dem Definitionsbereich \(D_{f} = [0;6]\). Der Punkt \(P(x|f(x))\), der Lotfußpunkt \(L(x|0)\) des Lotes von \(P\) auf die \(x\)-Achse und der Koordinatenursprung \(O\) legen das Dreieck \(OLP\) fest.
Bestimmen Sie die Koordinaten des Punktes \(P\), sodass der Flächeninhalt \(A\) des Dreiecks \(OLP\) maximal ist.
Aufgabe 4
Gegeben sind die Kugel \(K_{1}\) mit dem Mittelpunkt \(M_{1}(-3|5|8)\) und dem Radius \(r_{1} = 3\) sowie die Kugel \(K_{2}\) mit dem Mittelpunkt \(M_{2}(7|-5|3)\) und dem Radius \(r_{2} = 7\).
Untersuchen Sie die gegenseitige Lage der Kugeln \(K_{1}\) und \(K_{2}\) und berechnen Sie ggf. den Abstand der beiden Kugeln.
Aufgabe 5
Bei der Herstellung wiederaufladbarer Batterien treten zwei Fehler auf.
\(A\): Die Abmessung der Batterie weicht von der Typennorm ab.
\(L\): Die Ladekapazität der Batterie liegt 20 % unter dem Sollwert.
Laut Qualitätskontrolle weisen 15 % der Batterien den Fehler \(L\) auf und 5 % den Fehler \(A\). Die Wahrscheinlichkeit, dass mindestens einer der beiden Fehler auftritt, wird mit 17 % angegeben.
a) Beschreiben Sie folgende Ereignisse im Sachzusammenhang:
α) \(\overline{\overline{A} \cap \overline{L}}\)
β) \((A \cap \overline{L}) \cup (\overline{A} \cap L)\)
b) Erstellen Sie eine den Sachverhalt beschreibende vollständig ausgefüllte Vierfeldertaffel.
c) Zeigen Sie dass die Ereignisse \(A\) und \(L\) stochastisch abhängig sind.
d) Erstellen Sie ein vollständig ausgefülltes Baumdiagramm, beginnend mit dem Ereignis \(A\). Beschreiben Sie, woran sich die stochastische Abhängigkeit der Ereignisse \(A\) und \(L\) an diesem Baumdiagramm erkennen lässt.

