Der Verlauf des oberen Blattrands wird in der Nähe der Blattspitze durch das bisher verwendete Modell nicht genau genug dargestellt. Daher soll der obere Blattrand im Modell für \(-2 \leq x \leq 0\) nicht mehr durch \(G_h\), sondern durch den Graphen \(G_k\) einer in \(\mathbb R\) definierten ganzrationalen Funktion \(k\) dritten Grades beschrieben werden. Für die Funktion \(k\) werden die folgenden Bedingungen gewählt (\(k'\) und \(h'\) sind die Ableitungsfunktionen von \(k\) bzw. \(h\)):
\[\begin{align*} \sf{I} & \quad k(0) = h(0) \\[0.8em] \sf{II} & \quad k'(0) = h'(0) \\[0.8em] \sf{III} & \quad k(-2) = h(-2) \\[0.8em] \sf{IV} & \quad k'(-2) = 1{,}5 \end{align*}\]
Begründen Sie im Sachzusammenhang, dass die Wahl der Bedingungen I, II und III sinnvoll ist. Machen Sie plausibel, dass die Bedingung IV dazu führt, dass die Form des Blatts in der Nähe der Blattspitze im Vergleich zum ursprünglichen Modell genauer dargestellt wird.
(3 BE)
Lösung zu Teilaufgabe 3c
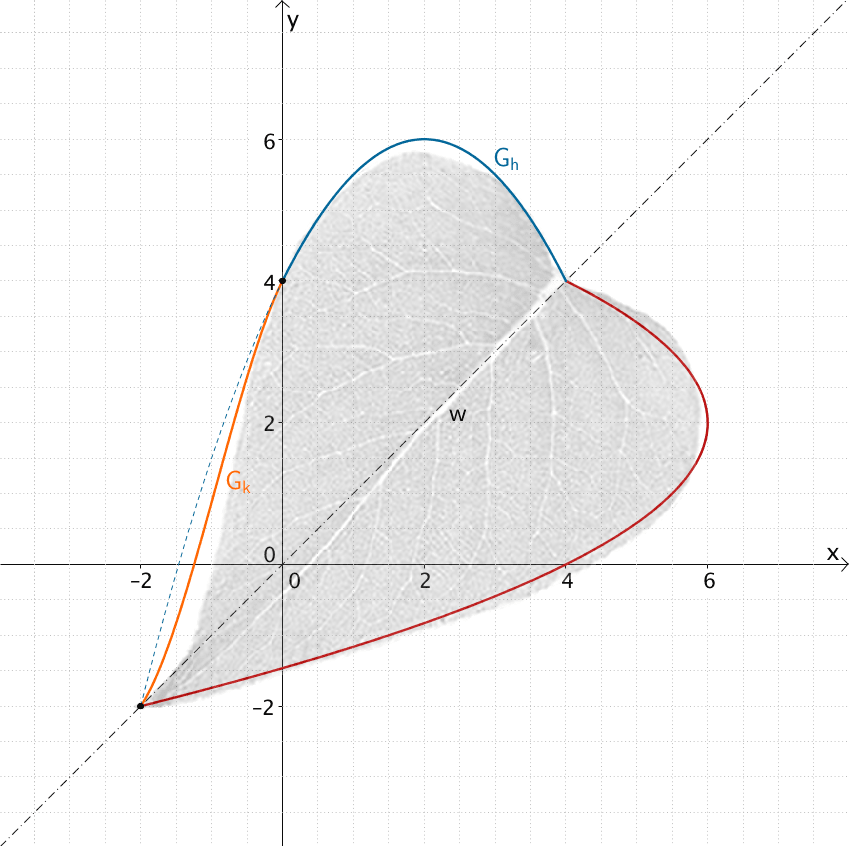
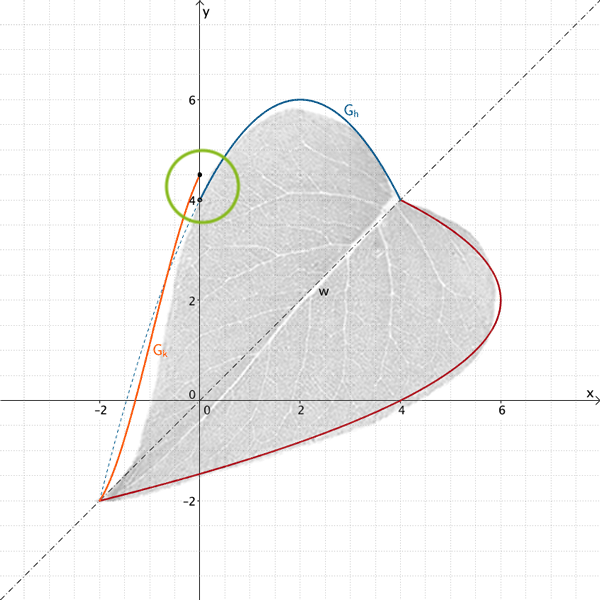
\(G_{k}\) für \(-2 \leq x \leq 0\), \(G_h\) für \(0 < x \leq 4\), an der Winkelhalbierenden \(w\) gespiegelter Bildgraph \(G_{h}^{*}\) von \(G_{h}\)
Anmerkung: Die Abbildung zeigt für \(-2 \leq x \leq 0\) den Graph der ganzrationalen Funktion \(k\) dritten Grades, welcher die Bedingungen I, II, III und IV erfüllt. Die Ergänzung (nicht Teil der Prüfung!) „Bestimmung des Funktionsterms von \(k\)" beschreibt die Vorgehensweise.
Begründung im Sachzusammenhang, dass die Wahl der Bedingung I, II und III sinnvoll ist
Begründung für Bedingung I und III
\[\begin{align*} \sf{I} & \quad k(0) = h(0) \\[0.8em] \sf{III} & \quad k(-2) = h(-2) \end{align*}\]
Der Graph \(G_h\) des ursprüngliche Modells beschreibt den oberen Blattrand im Punkt \((0|h(0))\) und die Blattspitze im Punkt \((-2|h(-2))\) sehr genau.
Bedingung I garantiert an der Stelle \(x = 0\) einen lückenlosen Übergang der beiden Graphen \(G_{k}\) und \(G_{h}\).
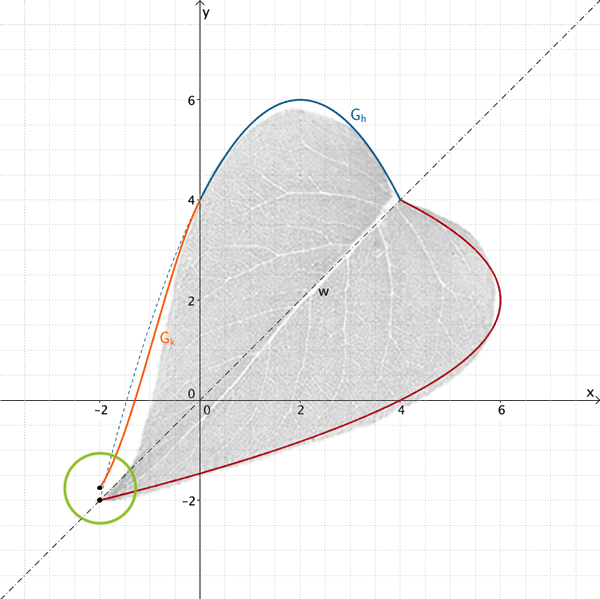
Der Punkt \((-2|h(-2))\) ist Fixpunkt der Spiegelung von \(G_{h}\) an der Winkelhalbierenden \(w\) und bildet im Modell die Blattspitze ab. Bedingung II garantiert, dass der Graph \(G_k\) an der Stelle \(x = -2\) lückenlos an das Spiegelbild von \(G_{h}\) anschließt, damit das genauere Modell die Blattspitze abbilden kann.
\(\Longrightarrow \quad \) Bedingung I und III ist sinnvoll.
Beispiele für \(k(0) \neq h(0)\) bzw. \(k(-2) \neq h(-2)\) (nicht verlangt):
\[k(0) \neq h(0)\]
Der Graph, der den oberen Blattrand an der „Nahtstelle" \(x = 0\) beschreibt, hat einen endlichen Sprung.
\[k(-2) \neq h(-2)\]
Der Graph, der die Blattspitze an der „Nahtstelle" \(x = -2\) beschreibt, hat einen endlichen Sprung.
Begründung für Bedingung II
\[\sf{II} \quad k'(0) = h'(0)\]
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
Der Graph \(G_{h}\) des ursprünglichen Modells besitzt im Punkt \((0|h(0))\) die Steigung \(h'(0)\) (Steigung der Tangente an \(G_{h}\) im Punkt \((0|h(0))\)). Damit der Graph \(G_{k}\) des genaueren Modells an der Stelle \(x = 0\) „knickfrei" an den Graphen \(G_{h}\) anschließen kann, muss der Graph \(G_{k}\) an der Stelle \(x = 0\) ebenfalls die Steigung \(h'(0)\) besitzen.
\(\Longrightarrow \quad \) Bedingung II ist sinnvoll.
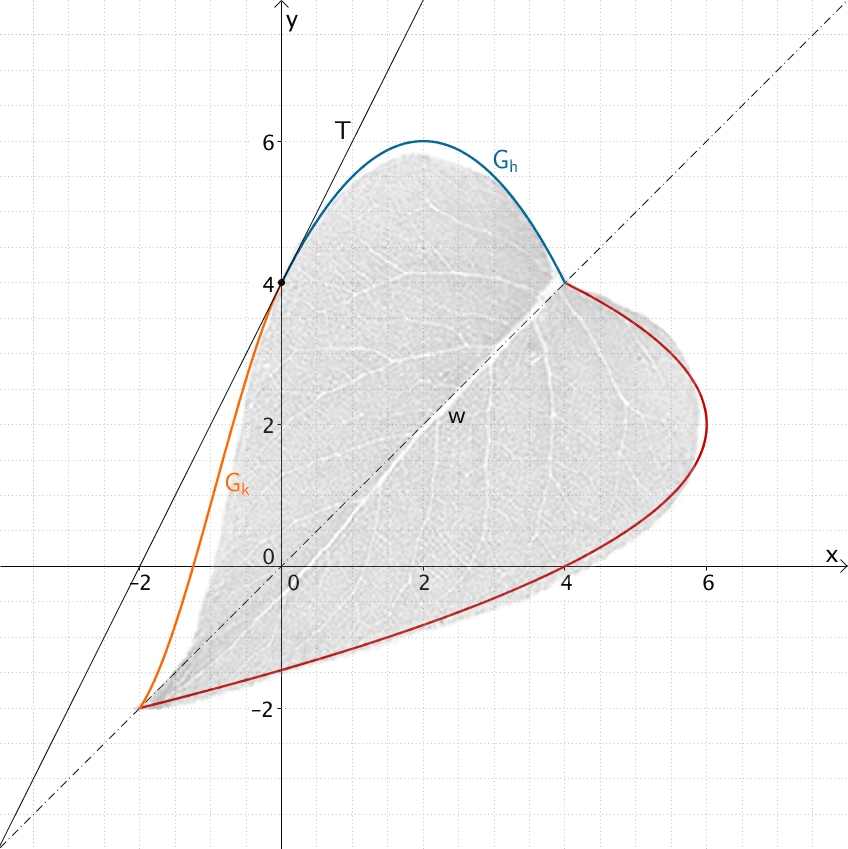
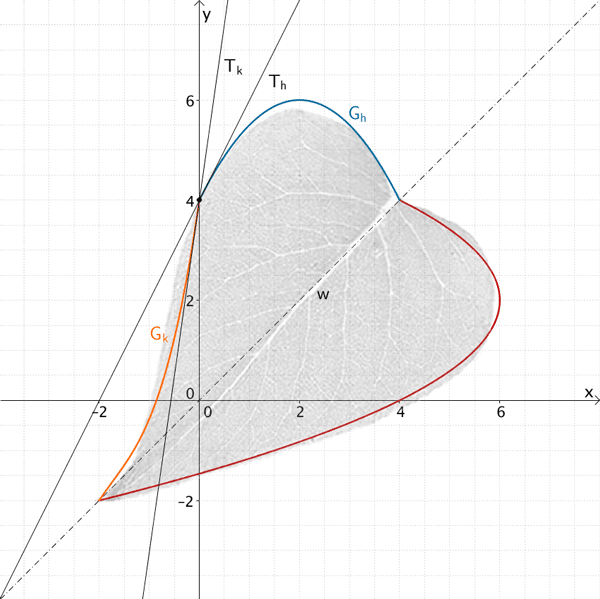
Der Graph \(G_{h}\) und der Graph \(G_{k}\) besitzt an der „Nahtstelle" \(x = 0\) dieselbe Steigung \(h'(0)\), Steigung der Tangente \(T\) an \(G_{h}\) bzw. \(G_{k}\) im Punkt \((0|h(0))\)
Beispiele für \(k'(0) \neq h'(0)\) (nicht verlangt):
\[k('0) \neq h'(0)\]
Die Steigung der Tangente \(T_{k}\) an \(G_{k}\) an der „Nahtstelle" \(x = 0\) ist ungleich der Steigung der Tangente \(T_{h}\) an \(G_{h}\). Der Graph, der für \(-2 \leq x \leq 4\) den oberen Blattrand beschreibt, hat an der Stelle \(x = 0\) einen Knick.
Erläuterung, weshalb die Bedingung IV die Blattspitze genauer darstellt
\[\sf{IV} \quad k'(-2) = 1{,}5\]
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
Das ursprüngliche Modell nähert den Ansatz des oberen Blattrands an der Blattspitze durch \(G_{h}\) mit der Steigung 4 an (siehe Teilaufgabe 3b, Tangente an \(G_{h}\) im Punkt \((-2|h(-2))\)).
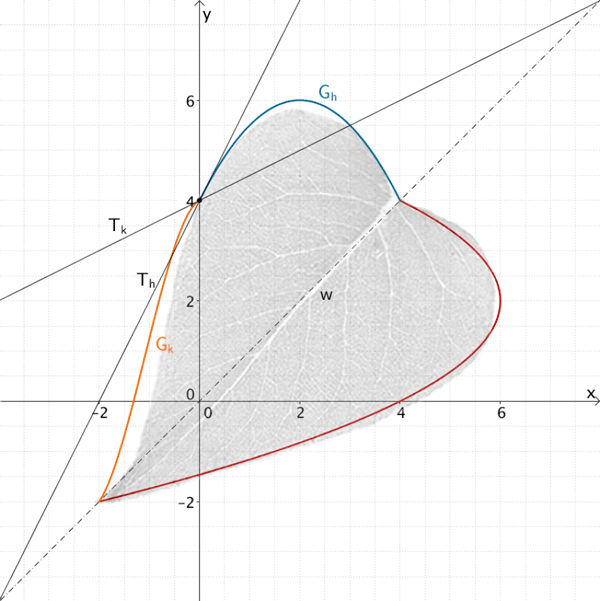
Die Form des Blattes an der Blattspitze lässt dagegen erkennen, dass die Beschreibung des oberen Blattrands in der Nähe der Blattspitze sich an der Steigung 1 der Winkelhalbierenden \(w\) orientieren sollte. Die Bedingung \(k'(-2) = 1,5\) für einen flacheren Verlauf von \(G_{k}\) an der Stelle \(x = -2\) stellt deshalb die Form des Blattes an der Blattspitze im Vergleich zum ursprünglichen Modell genauer dar.
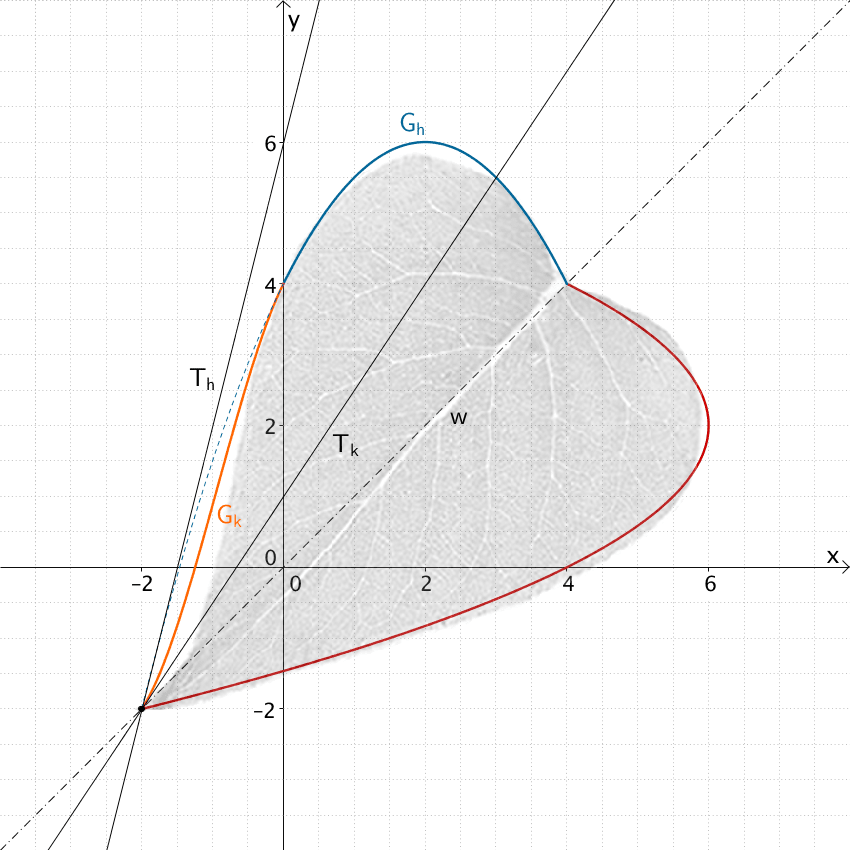
Der Graph \(G_k\) mit der Steigung \(m_{T_{k}} = k'(-2) = 1{,}5\) an der Stelle \(x = -2\) stellt die Form des Blattes an der Blattspitze genauer dar als der Graph \(G_{h}\) mit der Steigung \(m_{T_{h}} = h'(-2) = 4\) (siehe Teilaufgabe 3b).
Ergänzung: Bestimmung des Funktionsterms von \(k\)
Die nachfolgende Ergänzung ist nicht Teil der Prüfung! Sie soll dem besseren Verständnis für die in die Aufgabenstellung beschriebene Funktion \(k\) unter den Bedingungen I, II, III und IV dienen.
Laut Angabe soll \(G_k\) für \(-2 \leq x \leq 0\) der Graph einer in \(\mathbb R\) definierten ganzrationalen Funktion \(k\) dritten Grades sein, welche die Bedingungen I, II, III und IV erfüllt.
\[\begin{align*} \sf{I} & \quad k(0) = h(0) \\[0.8em] \sf{II} & \quad k'(0) = h'(0) \\[0.8em] \sf{III} & \quad k(-2) = h(-2) \\[0.8em] \sf{IV} & \quad k'(-2) = 1{,}5 \end{align*}\]
Ansatz formulieren:
\[k(x) = ax^3 + bx^2 + cx + d\,; \quad a, b, c, d \in \mathbb R\,, \enspace a \neq 0\]
Bedingungen formulieren:
\[k(x) = ax^3 + bx^2 + cx + d; \quad h(x) = -\frac{1}{2}x^2 + 2x + 4\]
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[k'(x) = 3ax^2 + 2bx + c\,; \quad h'(x) = -x + 2\]
\[\begin{align*} \sf{I} & & k(0) &= h(0) \\[0.8em] & & a \cdot 0^3 + b \cdot 0^2 + c \cdot 0 + d &= -\frac{1}{2} \cdot 0^2 + 2 \cdot 0 + 4 \\[0.8em] & & d &= 4 \\[3.2em] \sf{II} & & k'(0) &= h'(0) \\[0.8em] & & 3a \cdot 0^2 + 2b \cdot 0 + c &= -0 + 2 \\[0.8em] & & c &= 2 \\[3.2em] \sf{III} & & k(-2) &= h(-2) \\[0.8em] & & a \cdot (-2)^3 + b \cdot (-2)^2 + c \cdot (-2) + d &= -\frac{1}{2} \cdot (-2)^2 + 2 \cdot (-2) + 4 \\[0.8em] & & -8a + 4b - 2c + d &= -2 - 4 + 4 & &| c = 2\,; \enspace d = 4 \\[0.8em] & & -8a + 4b - 2 \cdot 2 + 4 &= -2 \\[0.8em] & & -8a + 4b &= -2 \\[3.2em] \sf{IV} & & k'(-2) &= 1{,}5 \\[0.8em] & & 3a \cdot (-2)^2 + 2b \cdot (-2) + c &= 1{,}5 \\[0.8em] & & 12 a - 4b + c &= 1{,}5 & &| c= 2 \\[0.8em] & & 12a -4b +2 &= 1{,}5 \end{align*}\]
Es verbleiben zwei lineare Gleichungen für die noch zu bestimmenden Werte von \(a\) und \(b\).
Lineares Gleichungssystem formulieren:
\[\begin{align*} \text{I} & & -8a + 4b &= -2 \\[0.8em] \text{II} & & \wedge \enspace 12a - 4b + 2 &= 1{,}5 \end{align*}\]
Zur Lösung des Gleichungssystems bietet sich das Additionsverfahren an.
\[\begin{align*} \text{I} \; + \; \text{II} \;\colon \; 4a + 2 &= -0{,}5 & &| - 2 \\[0.8em] 4a &= -2{,}5 & &| : 4 \\[0.8em] a &= -\frac{5}{8} \end{align*}\]
\[\begin{align*} a = -\frac{5}{8} \; \text{in I}\;\colon \; (-8) \cdot \left( -\frac{5}{8} \right) + 4b &= -2 \\[0.8em] 5 + 4b &= -2 & &| - 5 \\[0.8em] 4b &= -7 & &| : 4 \\[0.8em] b &= -\frac{7}{4} \end{align*}\]
Funktionsterm von \(r\) formulieren:
\[r(x) = ax^3 + bx^2 + cx + d\]
\[a = -\frac{5}{8}\,; \enspace b = -\frac{7}{4}\,; \enspace c = 2\,; \enspace d = 4\]
\[\Longrightarrow \quad r(x) = -\frac{5}{8}x^3 - \frac{7}{4}x^2 + 2x + 4\]
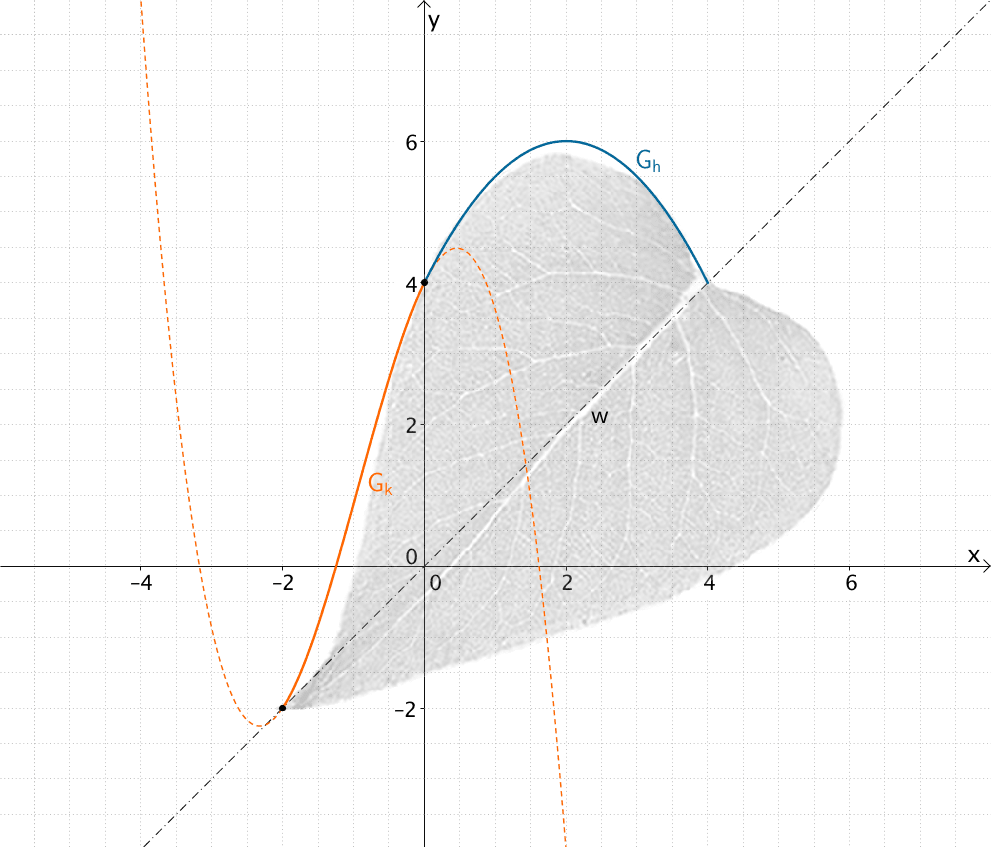
Graph \(G_{k}\) der ganzrationalen Funktion \(k\) dritten Grades (unter den Bedingungen I, II, III und IV), welcher den oberen Blattrand für \(-2 \leq x \leq 0\) im Falle des genaueren Modells beschreibt.