\(G_{f}\) und die \(x\)-Achse schließen im IV. Quadranten ein Flächenstück ein, das durch die Gerade \(g\) in zwei Teilflächen zerlegt wird. Berechnen Sie das Verhältnis der Flächeninhalte dieser beiden Teilflächen.
(6 BE)
Lösung zu Teilaufgabe 1d
Flächeninhaltsberechnung durch Integration
\[f(x) = x^{4} - 2x^{3}\,; \enspace D = \mathbb R\]
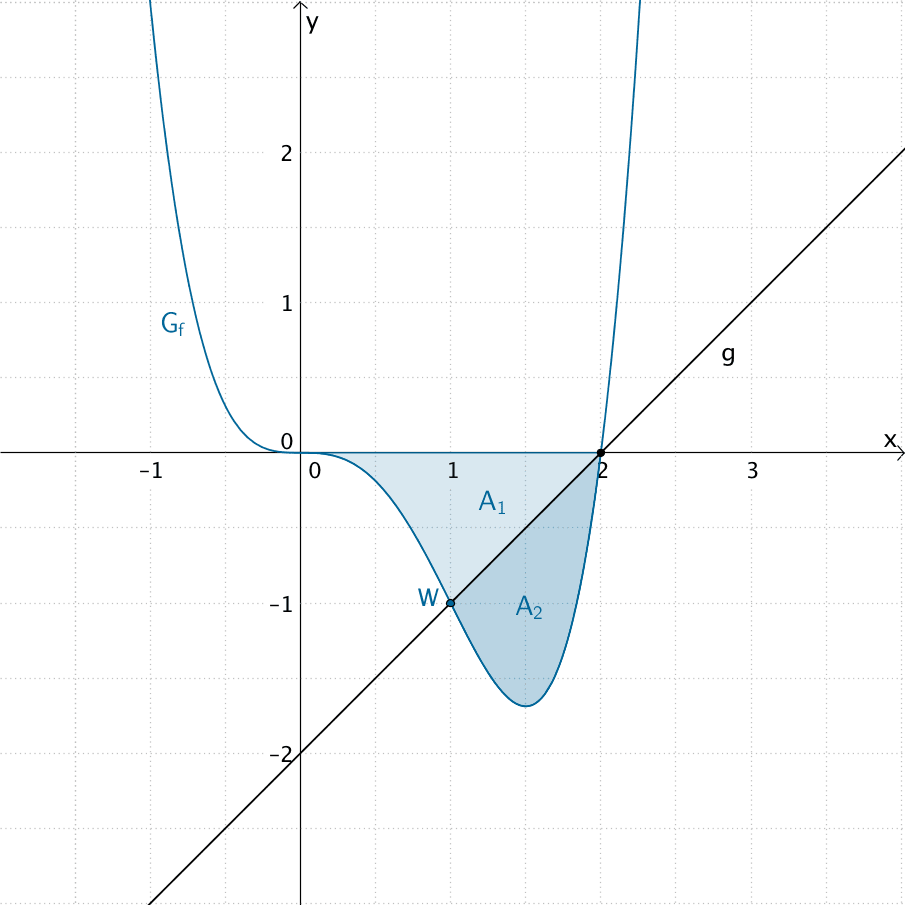
Flächenstück, das \(G_{f}\) und die \(x\)-Achse im IV. Quadranten einschließen und durch die Gerade \(g\) in zwei Teilflächen mit den Flächeninhalten \(A_{1}\) und \(A_{2}\) zerlegt wird.
Um das Verhältnis der Flächeninhalte \(A_{1}\) und \(A_{2}\) der beiden Teilflächen zu berechnen, bestimmt man zunächst den Flächeninhalt \(A = A_{1} + A_{2}\) des Flächenstücks, das \(G_{f}\) und die \(x\)-Achse im IV. Quadranten einschließen. Anschließend berechnet man einen der Flächeninhalte \(A_{1}\) oder \(A_{2}\). Der Flächeninhalt der jeweils zweiten Teilfläche ergibt sich durch Subtraktion: \(A_{1} = A - A_{2}\) bzw. \(A_{2} = A - A_{1}\).
Flächeninhalt \(A\) des Flächenstücks, das \(G_{f}\) und die \(x\)-Achse im IV. Quadranten einschließen
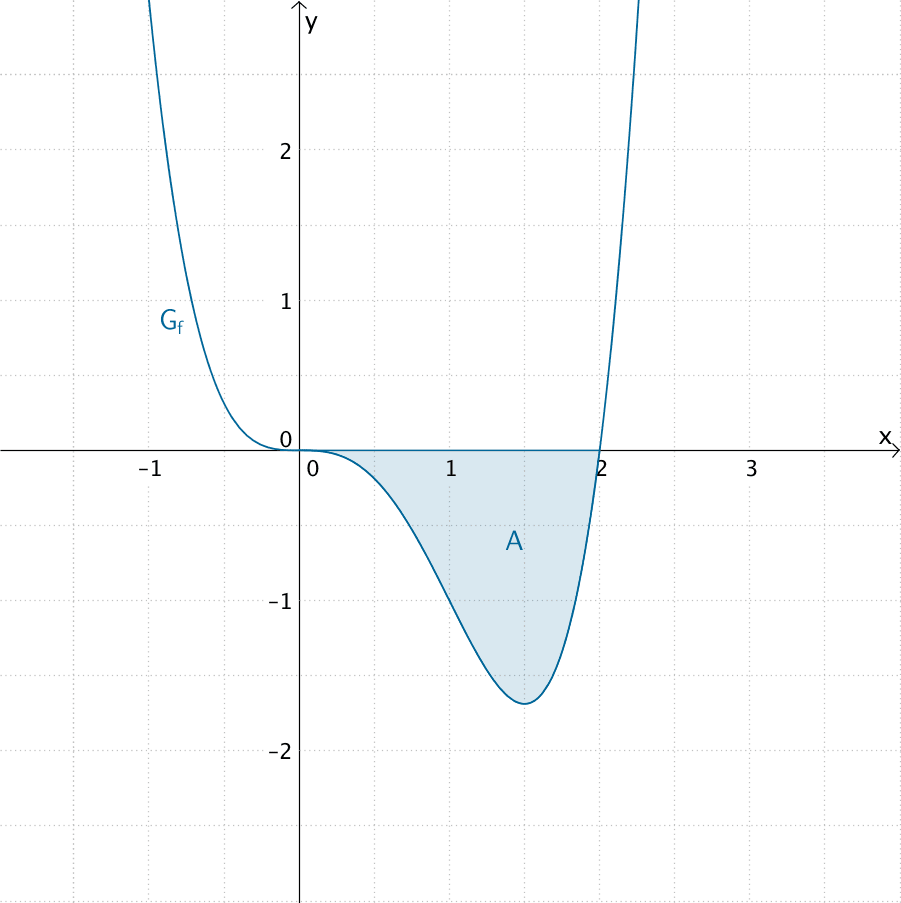
\[A = \left| \int_{0}^{2} f(x)\,dx \right|\]
Da \(G_{f}\) im IV. Quadranten unterhalb der \(x\)-Achse verläuft, ist der Wert des Integrals \(\displaystyle \int_{0}^{2} f(x)\,dx\) negativ. Für die Berechnung des Flächeninhalts \(A\) wird deshalb der Betrag des Integrals gewählt. Es ist ebenso möglich das Integral \(\displaystyle -\int_{0}^{2} f(x)\,dx\) zu berechnen.
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[A = \left| \int_{0}^{2} f(x)\,dx \right| = \left| F(2) - F(0) \right|\]
Stammfunktion \(F\) von \(f\) bestimmen:
\[f(x) = x^{4} - 2x^{3}\]
Stammfunktion einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad F(x) = \frac{1}{r + 1} \cdot x^{r + 1} + C\]
\[r \neq -1\]
\[F(x) = \frac{1}{5}x^{5} - \frac{1}{2}x^{4} + C\]
Flächeninhalt \(A\) berechnen:
\[\begin{align*} A &= \left| \int_{0}^{2} f(x)\,dx \right| \\[0.8em] &= \left| \int_{0}^{2} \left( x^{4} - 2x^{3} \right) dx \right| \\[0.8em] &= \left| \left[ \frac{1}{5}x^{5} - \frac{1}{2}x^{4} \right]_{0}^{2} \right| \\[0.8em] &= \left| \frac{1}{5} \cdot 2^{5} - \frac{1}{2} \cdot 2^{4} - \left( \frac{1}{5} \cdot 0^{5} - \frac{1}{2} \cdot 0^{4} \right) \right| \\[0.8em] &= \left| \frac{32}{5} - 8 - 0 \right| \\[0.8em] &= \left| -1{,}6 \right| \\[0.8em] &= 1{,}6 \end{align*}\]
Flächeninhalt \(A_{1}\) des Flächenstücks, das \(G_{f}\) und die Gerade \(g\) mit der \(x\)-Achse einschließen
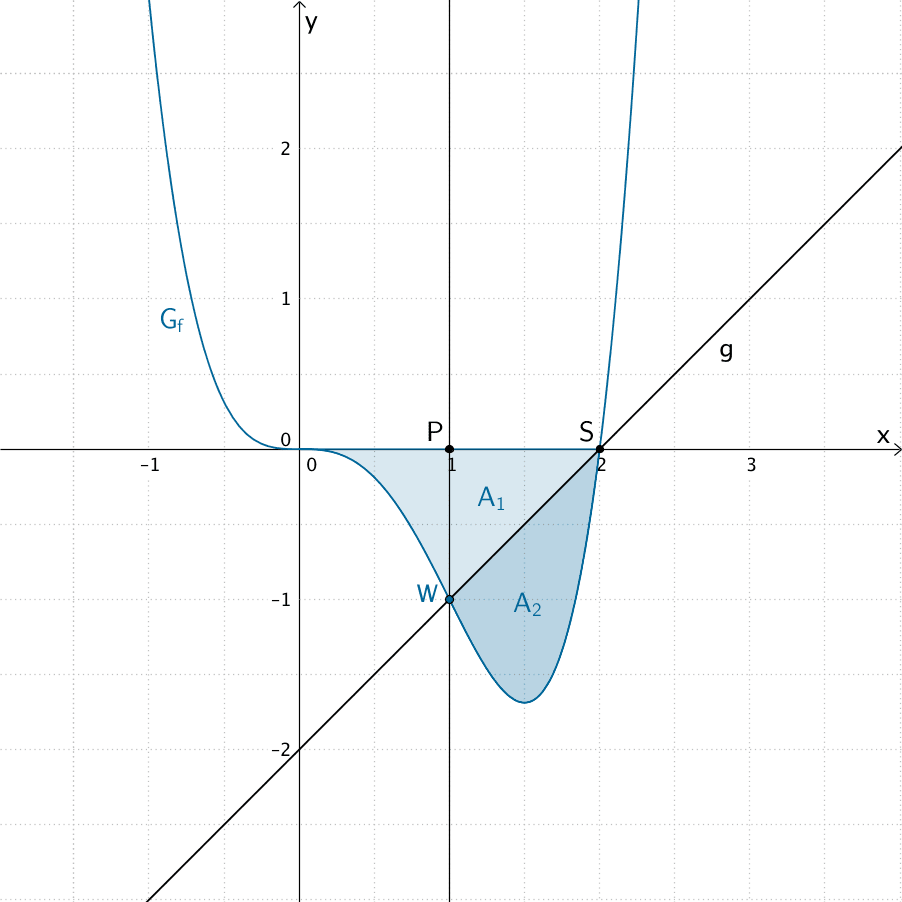
Die senkrechte Gerade \(x = 1\) durch den Wendepunkt \(W(1|-1)\) teilt das Flächenstück mit den Flächeninhalt \(A_{1}\). Der Flächeninhalt \(A_{1}\) setzt sich aus dem Flächeninhalt des Flächenstücks, das \(G_{f}\) im IV. Quadranten mit der \(x\)-Achse und der Gerade \(x = 1\) einschließt sowie dem Flächeninhalt des Dreiecks \(WSP\) zusammen.
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[A_{1} = \left| \int_{0}^{1} f(x) \, dx \right| + A_{WSP}\]
Stammfunktion \(F\) der Funktion \(f\):
\(F(x) = \frac{1}{5}x^{5} - \frac{1}{2}x^{4} + C\) (siehe oben, Flächeninhalt \(A\))
Flächeninhalt \(A_{1}\) berechnen:
\[\begin{align*} A_{1} &= \left| \int_{0}^{1} f(x) \, dx \right| + A_{WSP} \\[0.8em] &= \left| \int_{0}^{1} \left( x^{4} - 2x^{3} \right)dx \right| + A_{WSP} \\[0.8em] &= \left[ \frac{1}{5}x^{5} - \frac{1}{2}x^{4} \right]_{0}^{1} + A_{WSP} \\[0.8em] &= \left| \frac{1}{5} \cdot 1^{5} - \frac{1}{2} \cdot 1^{4} - 0 \right| + \frac{1}{2} \cdot 1 \cdot 1 \\[0.8em] &= \left| \frac{1}{5} - \frac{1}{2} \right| + \frac{1}{2} \\[0.8em] &= \left| \frac{2}{10} - \frac{5}{10} \right| + \frac{1}{2} \\[0.8em] &= \left| -\frac{3}{10} \right| + \frac{1}{2} \\[0.8em] &= \frac{3}{10} + \frac{5}{10} \\[0.8em] &= \frac{8}{10} \\[0.8em] &= 0{,}8 \end{align*}\]
Flächeninhalt \(A_{2}\) des Flächenstücks, das \(G_{f}\) und die Gerade \(g\) im IV. Quadranten einschließen
1. Möglichkeit: Dreieck \(WSP\) berücksichtigen

Der Flächeninhalt \(A_{2}\) ergibt sich aus dem Flächeninhalt des Flächenstücks, das \(G_{f}\) mit der \(x\)-Achse und der Geraden \(x = 2\) einschließt, abzüglich dem Flächeninhalt des Dreiecks \(WSP\).
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[A_{2} = \left| \int_{1}^{2} f(x) \, dx \right| - A_{WSP}\]
Stammfunktion \(F\) der Funktion \(f\):
\(F(x) = \frac{1}{5}x^{5} - \frac{1}{2}x^{4} + C\) (siehe oben, Flächeninhalt \(A\))
Flächeninhalt \(A_{2}\) berechnen:
\[\begin{align*} A_{2} &= \left| \int_{1}^{2} f(x)\,dx \right| - A_{WSP} \\[0.8em] &= \left| \int_{1}^{2} \left( x^{4} - 2x^{3} \right) dx \right| - A_{WSP} \\[0.8em] &= \left| \left[ \frac{1}{5}x^{5} - \frac{1}{2}x^{4} \right]_{1}^{2} \right| - A_{WSP} \\[0.8em] &= \left| \frac{1}{5} \cdot 2{5} - \frac{1}{2} \cdot 2^{4} - \left( \frac{1}{5} \cdot 1^{5} - \frac{1}{2} \cdot 1^{4} \right) \right| - \frac{1}{2} \\[0.8em] &= \left| \frac{32}{5} - \frac{16}{2} - \frac{1}{5} + \frac{1}{2} \right| - \frac{1}{2} \\[0.8em] &= \left| \frac{64}{10} - \frac{80}{10} - \frac{2}{10} + \frac{5}{10} \right| - \frac{1}{2} \\[0.8em] &= \left| -\frac{13}{10} \right| - \frac{1}{2} \\[0.8em] &= \frac{13}{10} - \frac{5}{10} \\[0.8em] &= \frac{8}{10} \\[0.8em] &= 0{,}8 \end{align*}\]
2. Möglichkeit: Differenzfunktion \(d = g - f\) integrieren
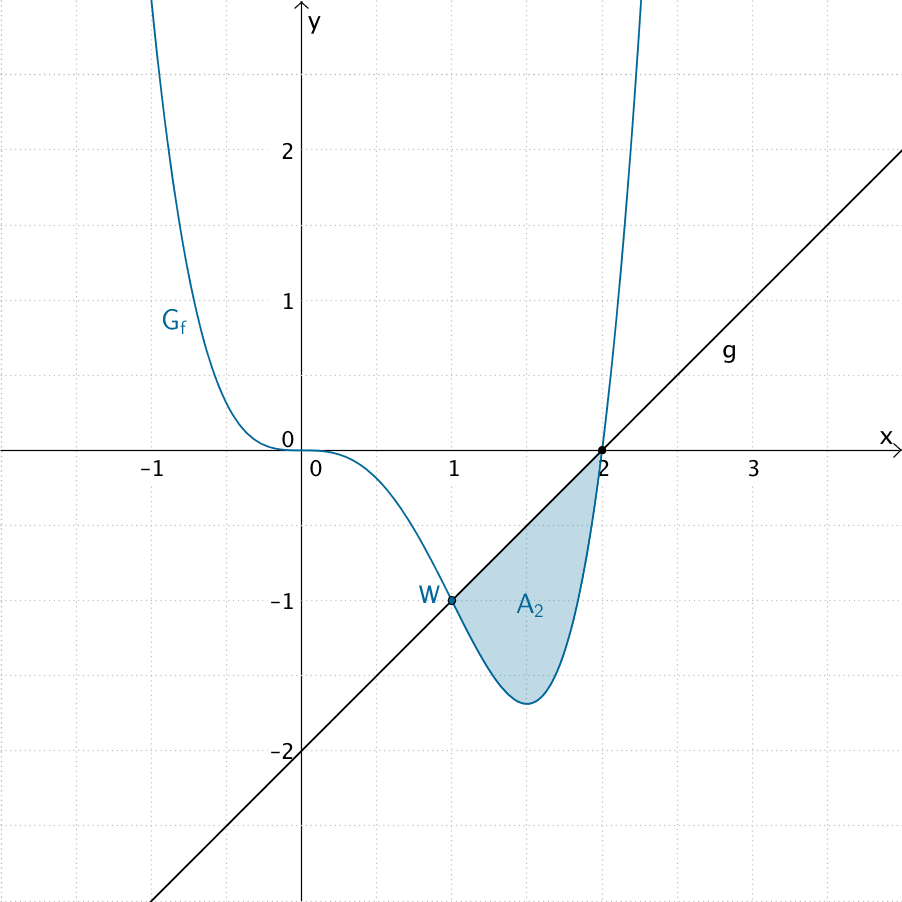
Die \(x\)-Koordinaten der Schnittpunkte \(W\,(1|-1)\) und \((2|0)\) von \(G_{f}\) und der Geraden \(g\) bilden die Integrationsgrenzen für den zu berechnenden Flächeninhalt \(A_{2}\) des Flächenstücks, das die Gerade \(g\) und \(G_{f}\) im IV. Quadranten einschließen.
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[A_{2} = \int_{1}^{2} [g(x) - f(x)]dx\]
Differenzfunktion \(d = g - f\) bilden:
\(g(x) = x - 2\) (siehe Teilaufgabe 1c)
\[f(x) = x^{4} - 2x^{3}\]
\[\begin{align*}d(x) &= g(x) - f(x) \\[0.8em] &= x - 2 - \left( x^{4} - 2x^{3}\right) \\[0.8em] &= -x^{4} + 2x^{3} + x - 2 \end{align*}\]
Stammfunktion \(D\) der Differenzfunktion \(d\) bestimmen:
\[d(x) = -x^{4} + 2x^{3} + x - 2\]
Stammfunktion einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad F(x) = \frac{1}{r + 1} \cdot x^{r + 1} + C\]
\[r \neq -1\]
\[D(x) = -\frac{1}{5}x^{5} + \frac{1}{2}x^{4} + \frac{1}{2}x^{2} - 2x + C\]
Flächeninhalt \(A_{2}\) berechnen:
\[\begin{align*} A_{2} &= \int_{1}^{2} [g(x) - f(x)]dx \\[0.8em] &= \int_{1}^{2}\left( -x^{4} + 2x^{3} + x - 2 \right) dx \\[0.8em] &= \left[ -\frac{1}{5}x^{5} + \frac{1}{2}x^{4} + \frac{1}{2}x^{2} - 2x \right]_{1}^{2} \\[0.8em] &= -\frac{1}{5} \cdot 2^{5} + \frac{1}{2} \cdot 2^{4} + \frac{1}{2} \cdot 2^{2} - 2 \cdot 2 \\[0.8em] &- \left( -\frac{1}{5} \cdot 1^{5} + \frac{1}{2} \cdot 1^{4} + \frac{1}{2} \cdot 1^{2} - 2 \cdot 1 \right) \\[0.8em] &= -\frac{32}{5} + 8 + 2 - 4 - \left( -\frac{1}{5} + \frac{1}{2} + \frac{1}{2} - 2 \right) \\[0.8em] &= -0{,}4 - (-1{,}2) \\[0.8em] &= 0{,}8 \end{align*}\]
Verhältnis der Flächeninhalte der beiden Teilflächen
\[\frac{A_{1}}{A_{2}} = \frac{A_{1}}{A - A_{1}} = \frac{0{,}8}{1{,}6 - 0{,}8} = \frac{0{,}8}{0{,}8} = \frac{1}{1}\]
\[\Longrightarrow \quad A_{1} = A_{2}\]
oder
\[\frac{A_{1}}{A_{2}} = \frac{A - A_{2}}{A_{2}} = \frac{1{,}6 - 0{,}8}{0{,}8} = \frac{0{,}8}{0{,}8} = \frac{1}{1}\]
\[\Longrightarrow \quad A_{1} = A_{2}\]
Die Gerade \(g\) teilt das Flächenstück, das \(G_{f}\) und die \(x\)-Achse im IV. Quadranten einschließen, in zwei gleich große Teilflächen.


