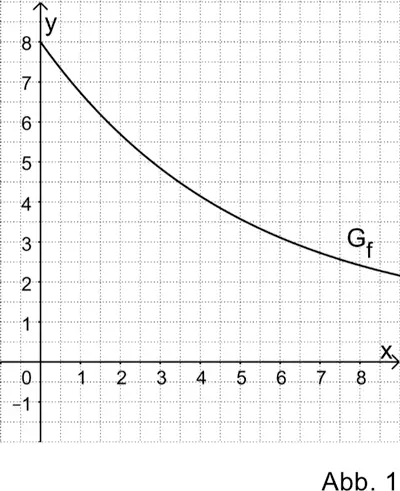
Gegeben ist die Funktion \(f \colon x \mapsto 1 + 7e^{-0{,}2x}\) mit Definitionsbereich \(\mathbb R_{0}^{+}\); die Abbildung 1 zeigt den Graphen \(G_{f}\).
Begründen Sie, dass die Gerade mit der Gleichung \(y = 1\) waagrechte Asymptote von \(G_{f}\) ist.
Zeigen Sie rechnerisch, dass \(f\) streng monoton abnehmend ist.
(3 BE)
Lösung zu Teilaufgabe 1a
\[f(x) = 1 + 7e^{-0{,}2x}; \; D_{f} = \mathbb R_{0}^{+}\]
Begründung, dass die Gerade mit der Gleichung \(y = 1\) waagrechte Asymptote von \(G_{f}\) ist
Da die waagrechte Asymptote das Verhalten von \(G_{f}\) im Unendlichen beschreibt, wird mit \(D_{f} = \mathbb R_{0}^{+} = [0;+\infty[\) die Grenzwertbetrachtung \(\lim \limits_{x\,\to\,+\infty}f(x)\) durchgeführt.
\[\begin{align*} \lim \limits_{x\,\to\,+\infty} f(x) &= \lim \limits_{x\,\to\,+\infty} \big( 1 + \textcolor{#cc071e}{\underbrace{7e^{\overbrace{-0{,}2x}^{\to\,-\infty}}}_{\to\,0}} \big) &&| \; \text{oder umformulieren mit}\; a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= \lim \limits_{x\,\to\,+\infty} \bigg( 1 + \textcolor{#cc071e}{\underbrace{\frac{7}{e^{0{,}2x}}}_{\to\,0}} \bigg) \\[0.8em] &= 1\end{align*}\]
\(\Longrightarrow \quad y = 1\) ist waagrechte Asymptote von \(G_{f}\).
Rechnerischer Nachweis, dass \(f\) streng monoton abnehmend ist
Gemäß dem Monotoniekriterium ist \(f\) streng monoton abnehmend, wenn für alle \(x \in D_{f}\) gilt: \(f'(x) < 0\).
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Erste Ableitung \(f'\) bilden:
Hierfür wird die Summenregel, die Faktorregel, die Kettenregel sowie die Ableitung der natürlichen Exponentialfunktion und die Ableitung einer Potenzfunktion benötigt.
\[f(x) = 1 + 7\textcolor{#0087c1}{e}^{\textcolor{#cc071e}{-0{,}2x}}; \; D_{f} = \mathbb R_{0}^{+}\]

Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
vgl. Merkhilfe
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
vgl. Merkhilfe
\[f'(x) = 0 + 7 \cdot \textcolor{#0087c1}{e}^{\textcolor{#cc071e}{-0{,}2x}} \cdot \textcolor{#cc071e}{(-0{,}2)} = \underbrace{-1{,}4\underbrace{e^{-0{,}2x}}_{>\,0}}_{<\,0}\]
\(\Longrightarrow \quad G_{f}\) ist in \(D_{f}\) streng monoton abnehmend.


