Gegeben ist ferner die in \(D_{h}\) definierte Integralfunktion \(\displaystyle H_{0} \colon x \mapsto \int_{0}^{x} h(t) \,dt\).
Begründen Sie ohne weitere Rechnung, dass folgende Aussagen wahr sind:
α) Der Graph von \(H_{0}\) ist streng monoton steigend.
β) Der Graph von \(H_{0}\) ist rechtsgekrümmt.
(4 BE)
Lösung zu Teilaufgabe 2b
Eigenschaften des Graphen einer Integralfunktion mithilfe des Graphen der Integrandenfunktion bestimmen
\[h(x) = \frac{3}{e^{x+1}-1}\,; \enspace D_{h} = ]-1;+\infty[\]
\[H_{0}(x) = \int_{0}^{x} h(t)\,dt\,; \enspace x \in D_{h}\]
Begründung für α) Der Graph von \(H_{0}\) ist streng monoton steigend.
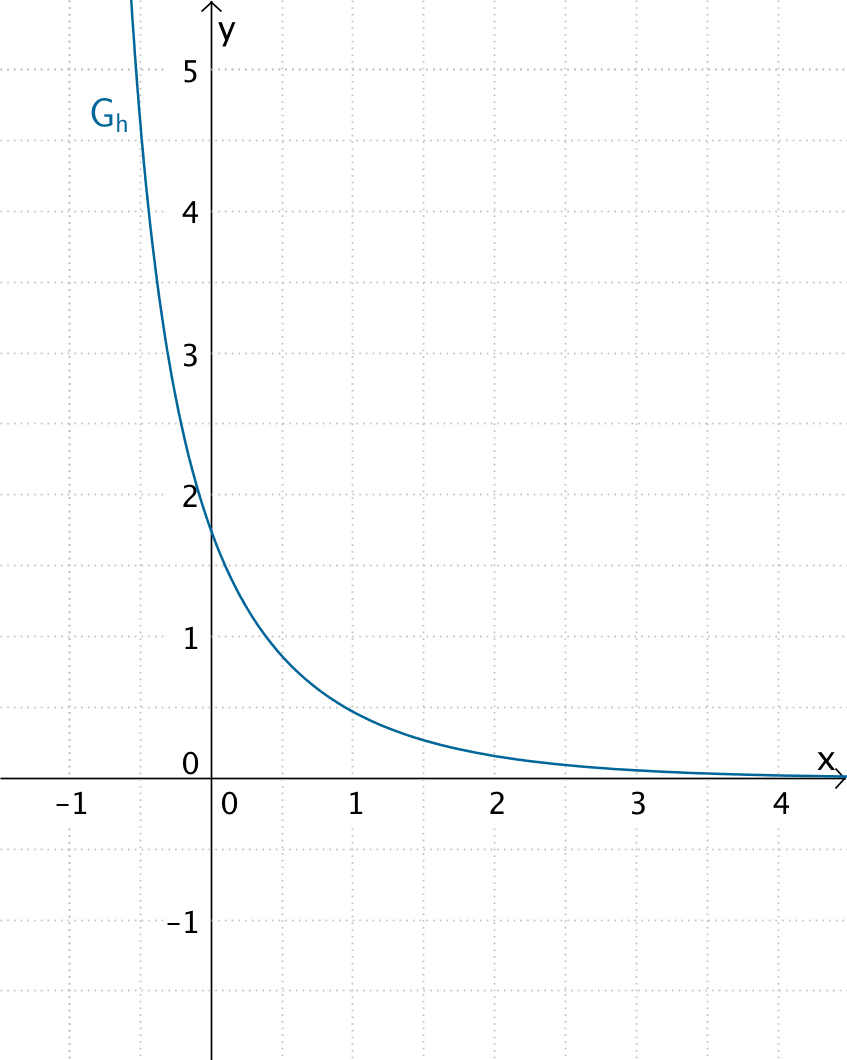
Der Graph der Funktion \(h\) verläuft für \(x \in D_{h}\) oberhalb der \(x\)-Achse.
Folglich gilt: \(h(x) > 0\).
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
Nach dem Hauptsatz der Differential- und Integralrechnung gilt:
\[H'_{0}(x) = h(x)\]
\[\left. \begin{align*} &h(x) > 0 \\ &H'_{0}(x) = h(x) \end{align*} \right\} \enspace \Rightarrow \enspace H'_{0}(x) > 0\]
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\(\Longrightarrow \quad\)Der Graph von \(H_{0}\) ist streng monoton steigend.
Begründung für β) Der Graph von \(H_{0}\) ist rechtsgekrümmt.
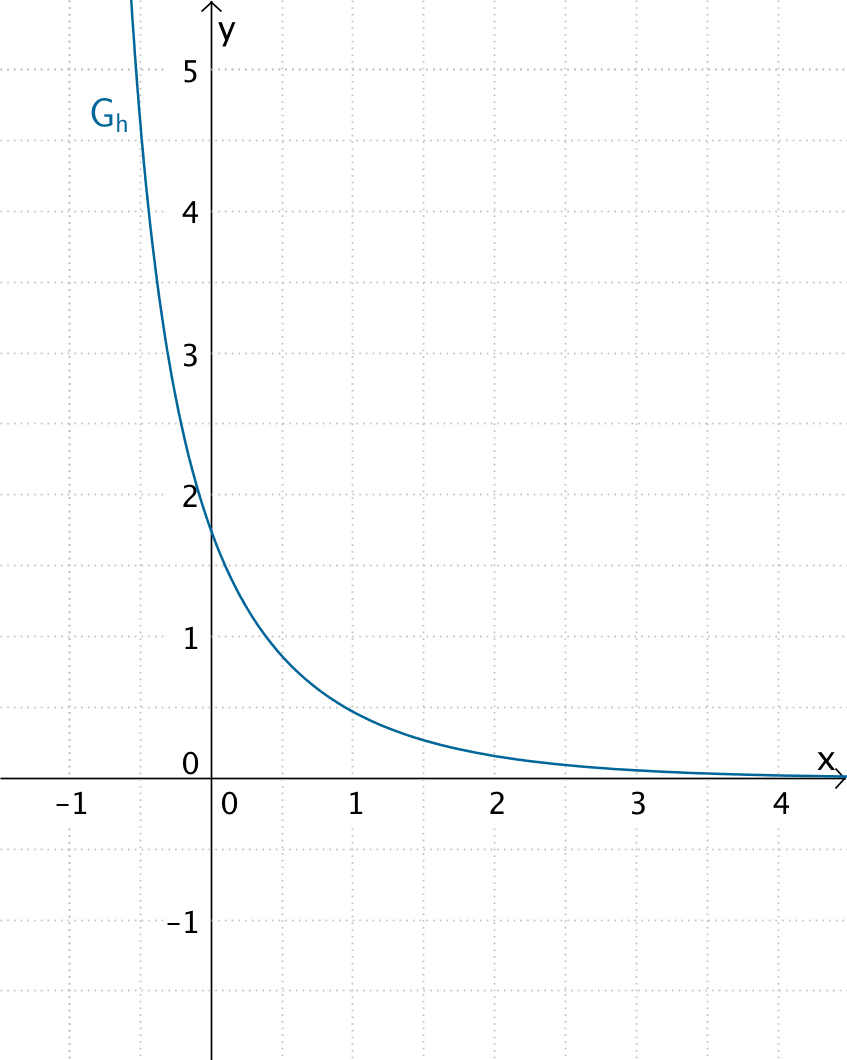
Der Graph der Funktion \(h\) ist für \(x \in D_{h}\) streng monoton fallend.
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Folglich gilt: \(h'(x) < 0\).
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
Nach dem Hauptsatz der Differential- und Integralrechnung gilt:
\[H''_{0}(x) = h'(x)\]
\[\left. \begin{align*} &h'(x) < 0 \\ &H''_{0}(x) = h'(x) \end{align*} \right\} \enspace \Rightarrow \enspace H''_{0}(x) < 0\]
Anwendung der Differentialrechnung:
Krümmungsverhalten von Funktionsgraphen
\(f''(x) < 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) rechtsgekrümmt.
\(f''(x) > 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) linksgekrümmt.
(vgl. Merkhilfe)
\(\Longrightarrow \quad\)Der Graph von \(H_{0}\) ist rechtsgekrümmt.


