Um die zeitliche Entwicklung des Flächeninhalts eines Algenteppichs am Nordufer des Sees zu beschreiben, wird im Term \(A(x)\) die im Exponenten zur Basis e enthaltene Zahl -0,2 durch eine kleinere Zahl ersetzt.
Vergleichen Sie den Algenteppich am Nordufer mit dem am Südufer
● hinsichtlich der durch \(A(0)\) und \(\lim \limits_{x\,\to\,+\infty} A(x)\) beschriebenen Eigenschaften (vgl. Aufgabe 2a).
● hinsichtlich der momentanen Änderungsrate des Flächeninhalts zu Beobachtungsbeginn (vgl. Aufgabe 2c).
Skizzieren Sie - ausgehend von diesem Vergleich - in der Abbildung 2 den Graphen einer Funktion, die eine mögliche zeitliche Entwicklung des Flächeninhalts des Algenteppichs am Nordufer beschreibt.
(5 BE)
Lösung zu Teilaufgabe 2f
Vergleich des Algenteppichs am Nordufer mit dem am Südufer
Vergleich hinsichtlich der durch \(A(0)\) und \(\lim \limits_{x\,\to\,+\infty} A(x)\) beschriebenen Eigenschaften
Es sei \(A_{k}\) die Funktion, welche die zeitliche Entwicklung des Flächeninhalts des Algenteppichs am Nordufer beschreibt.
Nordufer
\[A_{k}(x) = \frac{8}{1 + 7e^{kx}}; \; k < -0{,}2\]
\[A_{k}(\textcolor{#e9b509}{0}) = \frac{8}{1 + 7\underbrace{e^{k \cdot \textcolor{#e9b509}{0}}}_{1}} = 1\]
\[\lim \limits_{x\,\to\,+\infty} A_{k}(x) = \lim \limits_{x\,\to\,+\infty} \frac{8}{1 + 7\underbrace{e^{kx}}_{\to\,0}} = 8\]
Südufer
\[A(x) = \frac{8}{1 + 7e^{-0{,}2x}}\]
\(A(0) = 1\) (vgl. Teilaufgabe 2a)
\(\lim \limits_{x\,\to\,+\infty}A(x) = 8\) (vgl. Teilaufgabe 2a)
Schlussfolgerung:
Die Algenteppiche am Nord- und Südufer haben zu Beobachtungsbeginn den gleichen Flächeninhalt von 1 m². Im Laufe der Zeit erreicht der Flächeninhalt beider Algenteppiche jeweils einen Grenzwert von 8 m².
Vergleich hinsichtlich der momentanen Änderungsrate des Flächeninhalts zu Beobachtungsbeginn
Die Funktion \(A'_{k}\) beschreibt die momentane Änderungsrate des Flächeninhalts des Algenteppichs am Nordufer.
Achtung!
In Teilaufgabe 2c wurde \(A'(x) = \dfrac{\textcolor{#cc071e}{11{,}2}e^{\textcolor{#e9b509}{-0{,}2}x}}{(1 + 7e^{\textcolor{#e9b509}{-0{,}2}x})^{2}}\) (Südufer) bestimmt.
Um \(\mathbf{A'_{\textcolor{#89ba17}{k}}(x)}\) (Nordufer) zu formulieren kann nicht einfach der Faktor \(\mathbf{\textcolor{#e9b509}{(-0{,}2)}}\) im Exponenten der Exponentialterme von \(\mathbf{A'(x)}\) durch \(\mathbf{\textcolor{#89ba17}{k}}\) ersetzt werden. Denn durch die Anwendung der Kettenregel auf \(e^{\textcolor{#e9b509}{-0{,}2}x}\) beim Ableiten von \(A(x)\) ist der Faktor \(\textcolor{#e9b509}{(-0{,}2)}\) auch im Faktor \(\textcolor{#cc071e}{11{,}2}\) enthalten (vgl. Teilaufgabe 2c, Ableitungsfunktion A'(x)).
Stattdessen ist \(A_{k}(x)\) abzuleiten.
Erste Ableitung \(A'_{k}\) bilden:
Der Funktionsterm \(A_{k}(x)\) lässt sich mithilfe der Quotientenregel und der Kettenregel sowie der Ableitung der natürlichen Exponentialfunktion ableiten.
\[A_{k}(x) = \frac{\textcolor{#0087c1}{8}}{\textcolor{#cc071e}{1 + 7e^{kx}}}; \; k < -0{,}2\]

Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
vgl. Merkhilfe
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
vgl. Merkhilfe
\[\begin{align*} A'_{k}(x) &= \frac{\textcolor{#0087c1}{0} \cdot \textcolor{#cc071e}{\left( 1 + 7e^{kx} \right)} - \textcolor{#0087c1}{8} \cdot \textcolor{#cc071e}{\big( 0 + 7}\overbrace{\textcolor{#cc071e}{e^{kx} \cdot k}}^{\text{Kettenregel}} \textcolor{#cc071e}{\big)}}{\left( \textcolor{#cc071e}{1 + 7e^{kx}} \right)^{2}} \\[0.8em] &= \frac{(-8) \cdot \left( 7ke^{kx} \right)}{\left( 1 + 7e^{kx} \right)^{2}} \\[0.8em] &= \frac{-56ke^{kx}}{\left( 1 + 7e^{kx} \right)^{2}}\end{align*}\]
Nordufer
\[A'_{k}(\textcolor{#e9b509}{0}) = \frac{-56k\overbrace{e^{k \cdot \textcolor{#e9b509}{0}}}^{1}}{\big( 1 + 7\underbrace{e^{k \cdot \textcolor{#e9b509}{0}}}_{1} \big)^{2}} = \frac{-56k}{8^{2}} = -\frac{7}{8}k\]
Südufer
\(A'(0) = 0{,}175\)
Vergleich Nordufer - Südufer
Für \(\textcolor{#e9b509}{k = -0{,}2}\) (Südufer) ergibt sich:
\[A'_{k}(0) = \underbrace{-\frac{7}{8} \cdot \textcolor{#e9b509}{(-0{,}2)}}_{\text{Vergleichsbasis Südufer}} = 0{,}175 = A'(0)\]
Für \(\textcolor{#89ba17}{k < -0{,}2}\) (Nordufer) folgt:
\[A'_{k}(0) = \underbrace{-\frac{7}{8} \cdot \textcolor{#89ba17}{k} > -\frac{7}{8} \cdot \textcolor{#e9b509}{(-0{,}2)}}_{\text{Vergleich Nord-, Südufer}} \quad \Longrightarrow \quad A'_{k}(0) > A'(0)\]
Beispiel für \(\textcolor{#89ba17}{k = -0{,}4}\):
\[A'_{k}(0) = -\frac{7}{8} \cdot \textcolor{#89ba17}{(-0{,}4)} = 0{,}35 > A'(0)\]
Schlussfolgerung:
Zu Beobachtungsbeginn ist die momentane Änderungsrate des Flächeninhalts des Algenteppichs am Nordufer größer als die momentane Änderungsrate des Flächeninhalts des Algenteppichs am Südufer.
Skizzieren des Graphen einer Funktion, die eine mögliche Zeitliche Entwicklung des Flächeninhalts des Algenteppichs am Nordufer beschreibt
Über den Verlauf des Graphen \(G_{A_{k}}\) (Nordufer) ist Folgendes bekannt:
● \(A_{k}(0) = 1\) bedeutet, dass der Graph \(G_{A_{k}}\) im Punkt \((0|1)\) beginnt.
● \(\textcolor{#e9b509}{\lim \limits_{x\,\to\,+\infty}A_{k}(x) = 8}\) bedeutet, dass der Graph \(G_{A_{k}}\) die Asymptote mit der Gleichung \(\textcolor{#e9b509}{y = 8}\) hat.
● \(A'_{k}(0) > A'(0)\) bedeutet, dass der Graph \(G_{A_{k}}\) im Punkt \((0|1)\) eine größere Steigung hat als der Graph \(G_{A}\) (Südufer, vgl. Teilaufgabe 2e).
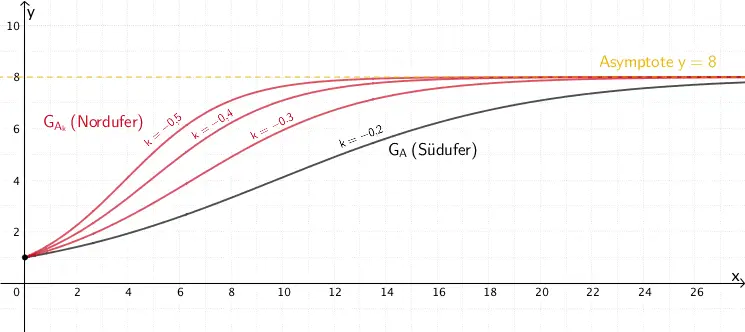
Graphen der Funktionen \(A_{k}\colon x \mapsto \dfrac{8}{1 + 7e^{kx}}\), die für \(k < -0{,}2\) eine mögliche zeitliche Entwicklung des Flächeninhalts des Algenteppichs am Nordufer beschreiben.


