Geben Sie die Nullstelle von \(H_{0}\) an und bestimmen Sie näherungsweise mithilfe von Abbildung 2 die Funktionswerte \(H_{0}(-0{,}5)\) sowie \(H_{0}(3)\). Skizzieren Sie in Abbildung 2 den Graphen von \(H_{0}\) im Bereich \(-0{,}5 \leq x \leq 3\).
(6 BE)
Lösung zu Teilaufgabe 2c
Nullstelle, Funktionswert (näherungsweise) und Skizzieren einer Integralfunktion
\[h(x) = \frac{3}{e^{x+1}-1}\,; \enspace D_{h} = ]-1;+\infty[\]
\[H_{0}(x) = \int_{0}^{x} h(t)\,dt\,; \enspace x \in D_{h}\]
Nullstelle der Integralfunktion \(H_{0}\)
Nullstelle einer Integralfunktion
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) besitzt an der unteren Integrationsgrenze \(x = a\) eine Nullstelle.
\[I_{a}(a) = \int_{a}^{a} f(t) \, dt = F(a) - F(a) = 0\]
\(F\) ist eine Stammfunktion von \(f\).
\[H_{0}(0) = \int_{0}^{0} h(t)\,dt = 0\]
\(x = 0\) ist Nullstelle der Integralfunktion \(H_{0}\).
Näherungsweise Bestimmung der Funktionswerte \(H_{0}(-0{,}5)\) sowie \(H_{0}(3)\) mithilfe von Abbildung 2
Funktionswert \(H_{0}(-0{,}5)\)
![Flächenstück, das der Graph der Funktion h im Intervall [-0,5;0] mit der x-Achse einschließt Flächenstück, das der Graph der Funktion h im Intervall [-0,5;0] mit der x-Achse einschließt](/images/stories/B2015_PT_B_A_1/B2015_PT_A_B_A_1_2c_1.png)
Der Funktionswert \(\displaystyle H_{0}(-0{,}5) = \int_{0}^{-0{,}5} h(t)\,dt\) ist gleich der negativen Maßzahl (da „nach links" integriert wird) des Flächeninhalts des Flächenstücks, das der Graph \(G_{h}\) der Funktion \(h\) im Intervall \([-0{,}5;0]\) mit der \(x\)-Achse einschließt.
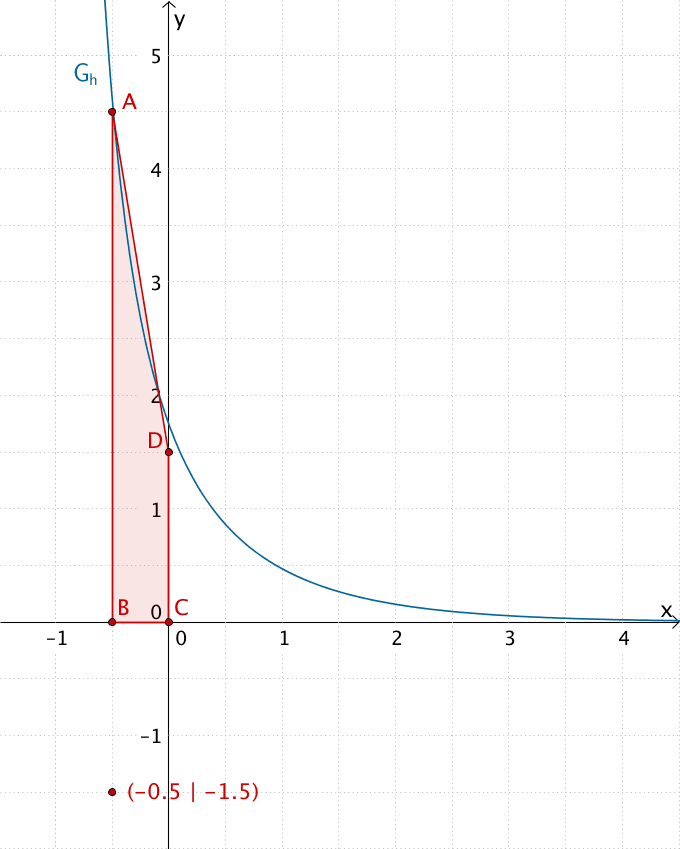
Das Flächenstück, das \(G_{h}\) im Intervall \([-0{,}5;0]\) mit der \(x\)-Achse einschließt, lässt sich näherungsweise durch das Trapez \(ABCD\) beschreiben, wobei die Grundlinien des Trapezes 4,5 LE (Längeneinheiten) bzw. 1,5 LE betragen und die Höhe des Trapezes 0,5 LE beträgt.
{snippet RG017}
\[\begin{align*} H_{0}(-0{,}5) &= \int_{0}^{-0{,}5} h(t)\,dt \\[0.8em] &\approx -A_{ABCD} \\[0.8em] &= -\left( \frac{4{,}5 + 1{,}5}{2} \cdot 0{,}5 \right) \\[0.8em] &= (-3) \cdot 0{,}5 = -1{,}5\end{align*}\]
Funktionswert \(H_{0}(3)\)
![Flächenstück, das der Graph der Funktion h im Intervall [0;3] mit der x-Achse einschließt. Flächenstück, das der Graph der Funktion h im Intervall [0;3] mit der x-Achse einschließt.](/images/stories/B2015_PT_B_A_1/B2015_PT_A_B_A_1_2c_3.png)
Der Funktionswert \(\displaystyle H_{0}(3) = \int_{0}^{3} h(t)\,dt\) ist gleich der Maßzahl des Flächeninhalts des Flächenstücks, das der Graph \(G_{h}\) der Funktion \(h\) im Intervall \([0;3]\) mit der \(x\)-Achse einschließt.
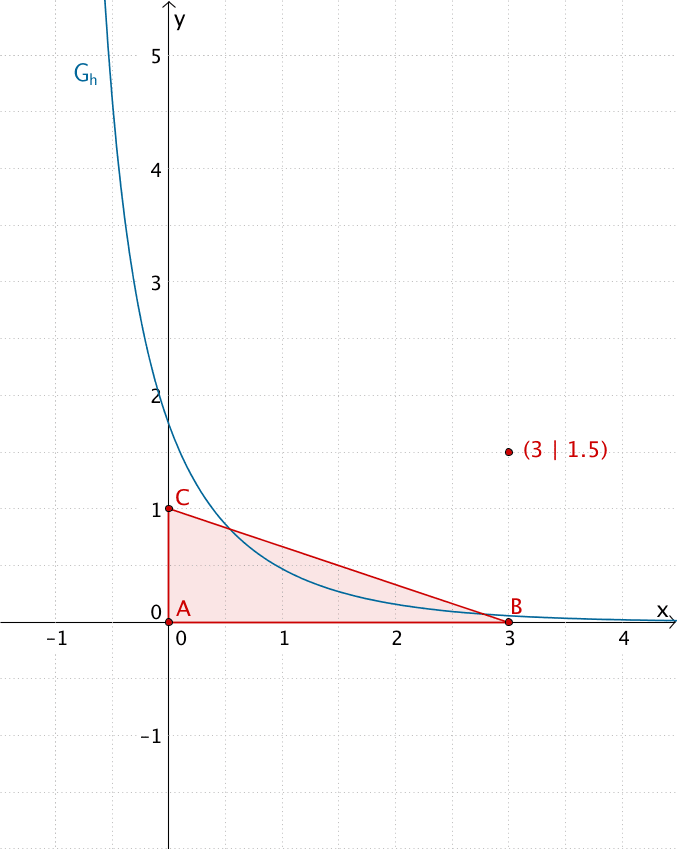
Das Flächenstück, das \(G_{h}\) im Intervall \([0;3]\) mit der \(x\)-Achse einschließt, lässt sich näherungsweise durch das Dreieck \(ABC\) beschreiben, wobei die Grundlinie des Dreiecks 3 LE (Längeneinheiten) und die Höhe des Dreiecks 1 LE beträgt.
\[\begin{align*} H_{0}(3) &= \int_{0}^{3} h(t)\,dt \\[0.8em] &\approx A_{ABC} \\[0.8em] &= \frac{1}{2} \cdot 3 \cdot 1 = 1{,}5\end{align*}\]
Skizzieren des Graphen von \(H_{0}\) im Bereich \(-0{,}5 \leq x \leq 3\)
Bisherige Ergebnisse aus Teilaufgabe 2c:
\[H_{0}(0) = 0\,; \enspace H_{0}(-0{,}5) \approx -1{,}5\,; \enspace H_{0}(3) \approx 1{,}5\]
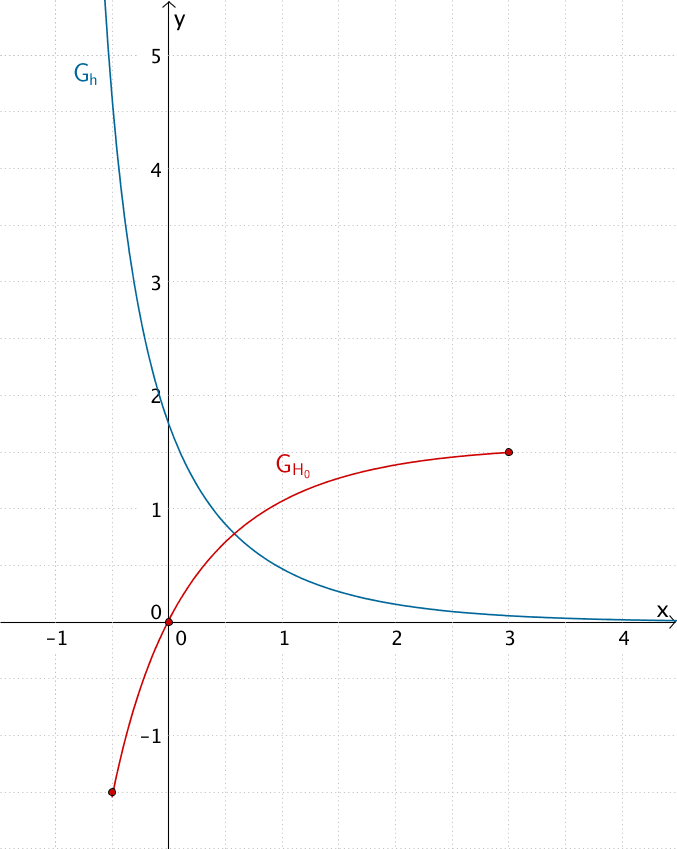
Verlauf (näherungsweise) des Graphen der Integralfunktion \(H_{0}\) im Bereich \(-0{,}5 \leq x \leq 3\)
Ergänzung: Steigung von \(G_{H_{0}}\)
Für das Skizzieren von \(G_{H_{0}}\) ist es hilfreich, zusätzlich zu den berechneten Funktionswerten, die Steigung von \(G_{H_{0}}\) an den Stellen \(x = -0{,}5\), \(x = 0\) und \(x = 3\) mithilfe von Abbildung 2 aus Aufgabe 2 näherungsweise zu ermitteln.
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
Nach dem Hauptsatz der Differential- und Integralrechnung gilt:
\[H'_{0}(x) = h(x)\]
Damit folgt für die Steigung der Tangente \(m_{T}\) an \(G_{H_{0}}\) in einem beliebigen Punkt \((x|H_{0}(x))\):
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[m_{T} = H'_{0}(x) = h(x)\]
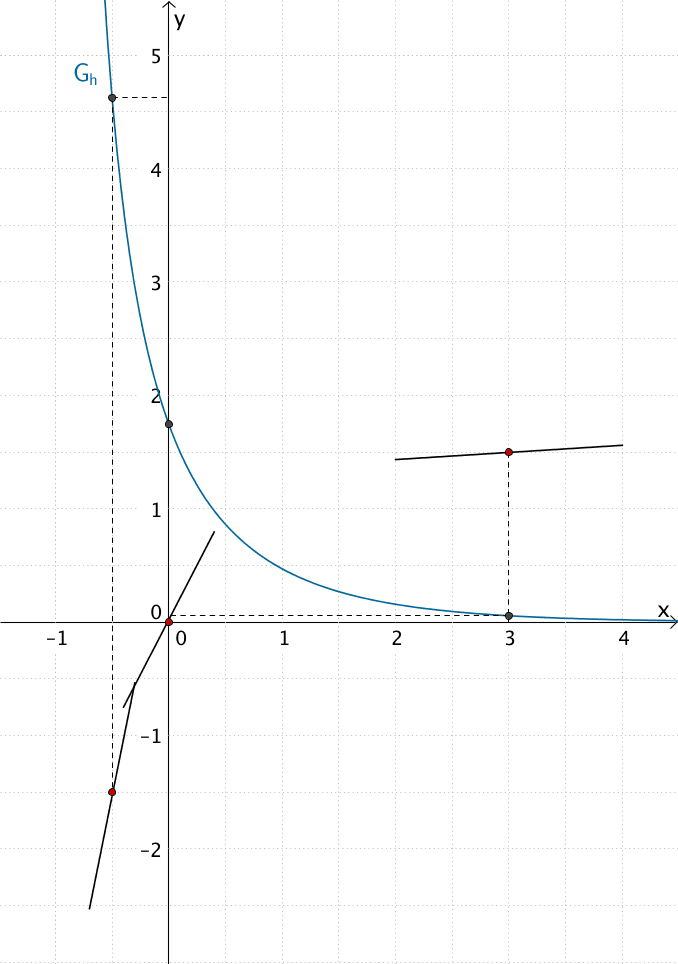
Tangenten an \(G_{H_{0}}\) an den Stellen \(x = -0{,}5\), \(x = 0\) und \(x = 3\)
Näherungsweise entnimmt man mithilfe von Abbildung 2 aus Aufgabe 2 die Steigungen der Tangenten.
An der Stelle \(x = -0{,}5\): \(m_{T} = H'_{0}(-0{,}5) = h(-0{,}5) \approx 4{,}6\)
An der Stelle \(x = 0\): \(m_{T} = H'_{0}(0) = h(0) \approx 1{,}75\)
An der Stelle \(x = 3\): \(m_{T} = H'_{0}(3) = h(3) \approx 0{,}1\)
Damit lässt sich der Verlauf des Graphen der Integralfunktion \(H_{0}\) etwas genauer skizzieren.
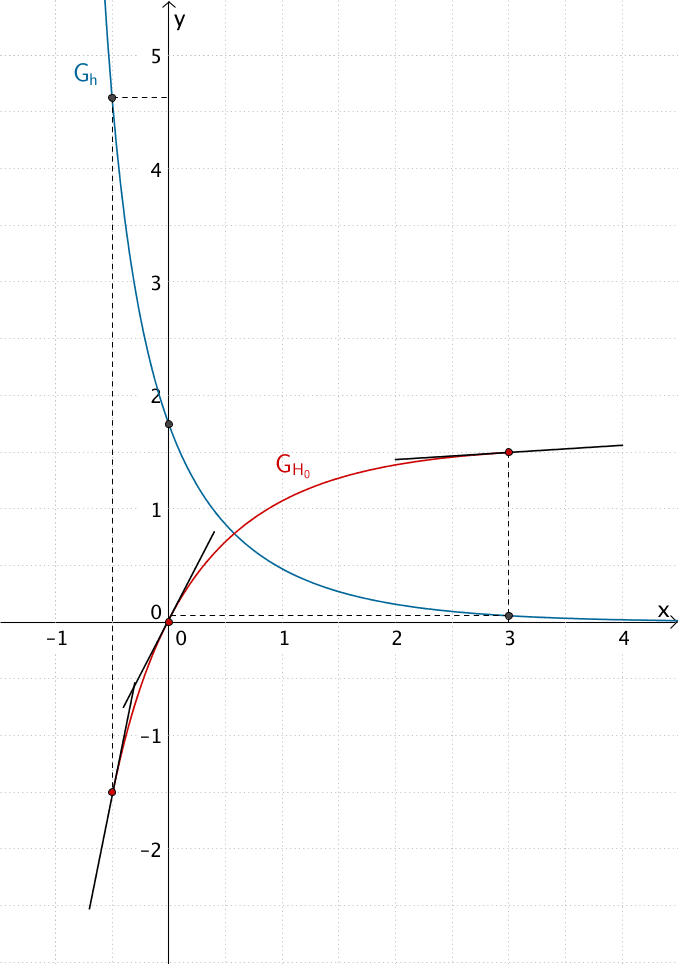
Verlauf (näherungsweise) des Graphen der Integralfunktion \(H_{0}\) im Bereich \(-0{,}5 \leq x \leq 3\) sowie der Tangenten (näherungsweise) an \(G_{H_{0}}\) an den Stellen \(x = -0{,}5\), \(x = 0\) und \(x = 3\)


