Gegeben sind die beiden bezüglich der \(x_{1}x_{3}\)-Ebene symmetrisch liegenden Punkte \(A(2|3|1)\) und \(B(2|-3|1)\) sowie der Punkt \(C(0|2|0)\).
Weisen Sie nach, dass das Dreieck \(ABC\) bei \(C\) rechtwinklig ist.
(3 BE)
Lösung zu Teilaufgabe 1a
Skalarprodukt orthogonaler Vektoren, Satz des Pythagoras, Umkreis eines rechtwinkligen Dreiecks (Thaleskreis)
1. Lösungsansatz: Skalarprodukt orthogonaler Vektoren
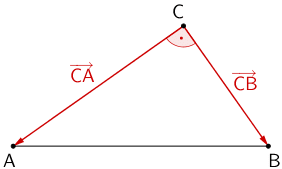
Planskizze: Das Dreieck \(ABC\) ist bei \(C\) rechtwinklig, wenn die Verbindungsvektoren \(\overrightarrow{CA}\) und \(\overrightarrow{CB}\) zueinander senkrecht sind, das heißt, wenn das Skalarprodukt der Vektoren gleich Null ist.
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\[\overrightarrow{CA} \circ \overrightarrow{CB} = 0 \quad \Longleftrightarrow \quad \overrightarrow{CA} \perp \overrightarrow{CB}\]
Verbindungsvektoren \(\overrightarrow{CA}\) und \(\overrightarrow{CB}\) bestimmen:
\(A(2|3|1)\), \(B(2|-3|1)\), \(C(0|2|0)\)
\[\overrightarrow{CA} = \overrightarrow{A} - \overrightarrow{C} = \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix} - \begin{pmatrix} 0 \\ 2 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix}\]
\[\overrightarrow{CB} = \overrightarrow{B} - \overrightarrow{C} = \begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix} - \begin{pmatrix} 0 \\ 2 \\ 0 \end{pmatrix} = \begin{pmatrix} 2 \\ -5 \\ 1 \end{pmatrix}\]
Orthogonalität der Vektoren \(\overrightarrow{CA}\) und \(\overrightarrow{CB}\) prüfen:
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \overrightarrow{CA} \circ \overrightarrow{CB} &= \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} \circ \begin{pmatrix} 2 \\ -5 \\ 1 \end{pmatrix} \\[0.8em] &= 2 \cdot 2 + 1 \cdot (-5) + 1 \cdot 1 \\[0.8em] &= 4 - 5 + 1 \\[0.8em] &= 0 \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{CA} \perp \overrightarrow{CB}\]
Schlussfolgerung:
Das Dreieck \(ABC\) ist bei \(C\) rechtwinklig.
2. Lösungsansatz: Satz des Pythagoras anwenden
Satzgruppe des Pythagoras im rechtwinkligen Dreieck
Satz des Pythagoras
\[\hspace{5px}a^2 + b^2 = c^2\]
Höhensatz
\[h^2 = p \cdot q\]
Kathetensatz
\[a^2 = c \cdot p\,; \enspace b^2 = c \cdot q\]
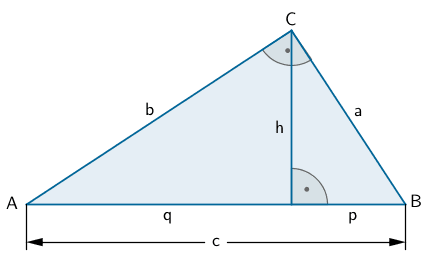
Das Dreieck \(ABC\) ist bei \(C\) rechtwinklig, wenn die Summe der Quadrate der Katheten \([CA]\) und \([BC]\) gleich dem Quadrat der Hypotenuse \([AB]\) ist.
Es ist also die Gültigkeit der Gleichung \(\overline{CA}^{2} + \overline{BC}^{2} = \overline{AB}^{2}\) zu überprüfen.
Längen der Seiten \([CA]\), \([BC]\) und \([AB]\) berechnen:
\(\overrightarrow{CA} = \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix},\; \overrightarrow{CB} = \begin{pmatrix} 2 \\ -5 \\ 1 \end{pmatrix}\) (vgl. 1. Lösungsansatz)
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\overline{CA} = \vert \overrightarrow{CA} \vert = \left| \begin{pmatrix} 2 \\ 1 \\ 1 \end{pmatrix} \right| = \sqrt{2^{2} + 1^{2} + 1^{2}} = \sqrt{6}\]
\[\overline{BC} = \vert \overrightarrow{BC} \vert = \left| \begin{pmatrix} 2 \\ -5 \\ 1 \end{pmatrix} \right| = \sqrt{2^{2} + (-5)^{2} + 1^{2}} = \sqrt{30}\]
\(A(2|3|1)\), \(B(2|-3|1)\)
\[\begin{align*}\overline{AB} &= \vert \overrightarrow{AB} \vert \\[0.8em] &= \vert \overrightarrow{B} - \overrightarrow{A} \vert \\[0.8em] &= \left| \begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix} - \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 0 \\ -6 \\ 0 \end{pmatrix} \right| \\[0.8em] &= \sqrt{0^{2} + (-6)^{2} + 0^{2}} \\[0.8em] &= 6 \end{align*}\]
Gültigkeit des Satzes des Pythagoras überprüfen:
Satzgruppe des Pythagoras im rechtwinkligen Dreieck
Satz des Pythagoras
\[\hspace{5px}a^2 + b^2 = c^2\]
Höhensatz
\[h^2 = p \cdot q\]
Kathetensatz
\[a^2 = c \cdot p\,; \enspace b^2 = c \cdot q\]

\[\begin{align*} \overline{CA}^{2} + \overline{BC}^{2} &= \overline{AB}^{2} \\[0.8em] {\sqrt{6}}^{2} + {\sqrt{30}}^{2} &= 6^{2} \\[0.8em] 6 + 30 &= 36 \qquad (\text{w}) \end{align*}\]
Schlussfolgerung:
Das Dreieck \(ABC\) ist bei \(C\) rechtwinklig.
3. Lösungsansatz: Umkreis eines rechtwinkligen Dreiecks (Thaleskreis)
Satz des Thales
Liegt der Punkt \(C\) eines Dreiecks \(ABC\) auf einem Kreis mit dem Durchmesser \([AB]\), ist der Winkel bei Punkt \(C\) ein rechter Winkel.
Der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks liegt immer in der Mitte der Hypotenuse.
![Das Dreieck ABC repräsentiert die Ebene E. Schnittkreis k der Ebene E und der Kugel K mit dem Durchmesser [AB] Das Dreieck ABC repräsentiert die Ebene E. Schnittkreis k der Ebene E und der Kugel K mit dem Durchmesser [AB]](/images/stories/B2017_PT_A_G_2/B2107_PT_A_G_2_1a_3.png)
Das Dreieck \(ABC\) repräsentiert die Ebene \(E\). Die gemeinsamen Punkte der Ebene \(E\) und einer Kugel \(K\) mit dem Durchmesser \([AB]\) liegen auf dem Schnittkreis \(k\).
Das Dreieck \(ABC\) ist bei \(C\) rechtwinklig, wenn der Punkt \(C\) auf dem Schnittkreis \(k\) liegt (Umkreis eines rechtwinkligen Dreiecks, Thaleskreis). Dies ist mit \(C \in E\) dann der Fall, wenn der Punkt \(C\) auf der Oberfläche der Kugel \(K\) liegt.
Es ist also die Punktprobe \(C \in K\) durchzuführen.
Gleichung der Kugel \(K\) formulieren:
Kugelgleichung
Eine Kugel mit dem Mittelpunkt \(M(m_{1}|m_{2}|m_{3})\) und dem Radius \(r\) wird beschrieben durch:
Vektordarstellung
\[(\overrightarrow{X} - \overrightarrow{M})^{2} = r^{2}\]
Koordinatendarstellung
\[(x_{1} - m_{1})^{2} + (x_{2} - m_{2})^{2} + (x_{3} - m_{3})^{2} = r^{2}\]
\[K \colon (x_{1} - m_{1})^{2} + (x_{2} - m_{2})^{2} + (x_{3} - m_{3})^{2} = r^{2}\]
MIt \(M_{[AB]} = \begin{pmatrix} m_{1} \\ m_{2} \\ m_{3} \end{pmatrix}\) und \(r = \frac{1}{2} \cdot \overline{AB}\)
Koordinaten des Mittelpunkts \(M_{[AB]}\) der Kugel \(K\) berechnen:
Mittelpunkt einer Strecke
Für den Ortsvektor \(\overrightarrow{M}\) des Mittelpunkts \(M\) einer Strecke \([AB]\) gilt:
\[\overrightarrow{M} = \frac{1}{2} \left( \overrightarrow{A} + \overrightarrow{B} \right)\]
\(A(2|3|1)\), \(B(2|-3|1)\)
\[\begin{align*} \overrightarrow{M_{[AB]}} &= \frac{1}{2} \cdot \left( \overrightarrow{A} + \overrightarrow{B} \right) \\[0.8em] &= \frac{1}{2} \cdot \left[ \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix} + \begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix} \right] \\[0.8em] &= \frac{1}{2} \cdot \begin{pmatrix} 4 \\ 0 \\ 2 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad M_{[AB]}(2|0|1)\]
Zu diesem Ergebnis gelangt man auch durch Überlegung: Da die Punkte \(A(2|3|1)\) und \(B(2|-3|1)\) symmetrisch bezüglich der \(x_{1}x_{2}\)-Ebene liegen (vgl. Angabe Aufgabe 1), muss die \(x_{2}\)-Koordinate des Mittelpunkts \(M_{[AB]}\) der Strecke \([AB]\) gleich Null sein und die \(x_{1}\)- bzw. die \(x_{3}\)-Koordinate mit den Koordinaten von \(A\) bzw. \(B\) übereinstimmen.
Radius \(r\) der Kugel \(K\) berechnen:
\(\overline{AB} = 6\) (vgl. 2. Lösungsansatz)
\[r = \frac{1}{2} \cdot \overline{AB} = \frac{1}{2} \cdot 6 = 3\]
Damit ergibt sich die Gleichung der Kugel \(K\) zu:
\[K \colon (x_{1} - m_{1})^{2} + (x_{2} - m_{2})^{2} + (x_{3} - m_{3})^{2} = r^{2}\]
\[M_{[AB]}(2|0|1)\]
\[r = 3\]
\[K \colon (x_{1} -2 )^{2} + (x_{2} - 0)^{2} + (x_{3} - 1)^{2} = 3^{2}\]
Punktprobe \(C \in K\) durchführen:
\(C(0|2|0)\)
\[\begin{align*} C \in K \colon (0 - 2)^{2} + (2 - 0)^{2} + (0 - 1)^{2} &= 3^{2} \\[0.8em] 4 + 4 + 1 &= 9 \\[0.8em] 9 &= 9 \qquad (\text{w}) \end{align*}\]
\[\Longrightarrow \quad C \in K\]
Schlussfolgerung:
Das Dreieck \(ABC\) ist bei \(C\) rechtwinklig.


