An einer Messstation wurde über einen Zeitraum von 10 Stunden die Anzahl der Pollen in einem Kubikmeter Luft ermittelt. Dabei kann die Anzahl der Pollen in einem Kubikmeter Luft zum Zeitpunkt \(t\) (in Stunden nach Beginn der Messung) durch die Gleichung \(n(t) = 3t^{2} - 60t + 500\) beschrieben werden.
Bestimmen Sie die mittlere Änderungsrate der Anzahl der Pollen in einem Kubikmeter Luft während der ersten beiden Stunden der Messung.
(3 BE)
Lösung zu Teilaufgabe 4a
Mittlere Änderungsrate im Sachzusammenhang
\[n(t) = 3t^{2} - 60t + 500\]
\[t \in [0;2]\]
Die mittlere Änderungsrate der Anzahl der Pollen in einem Kubikmeter Luft während der ersten beiden Stunden der Messung entspricht der Steigung \(m_{S}\) einer gedachten Geraden (Sekante) durch die Punkte \((0|n(0))\) und \((2|n(2))\) des Graphen \(G_{n}\) der Funktion \(n(t)\) (Einheit: \(\frac{1}{\sf{h}}\)).
Die gesuchte mittlere Änderungsrate gibt für die ersten beiden Stunden der Messung die durchschnittliche Änderung der Anzahl der Pollen pro Stunde in einem Kubikmeter Luft an (Zunahme: positive mittlere Änderungsrate, Abnahme: negative mittlere Änderungsrate).
Differenzenquotient oder mittlere Änderungsrate
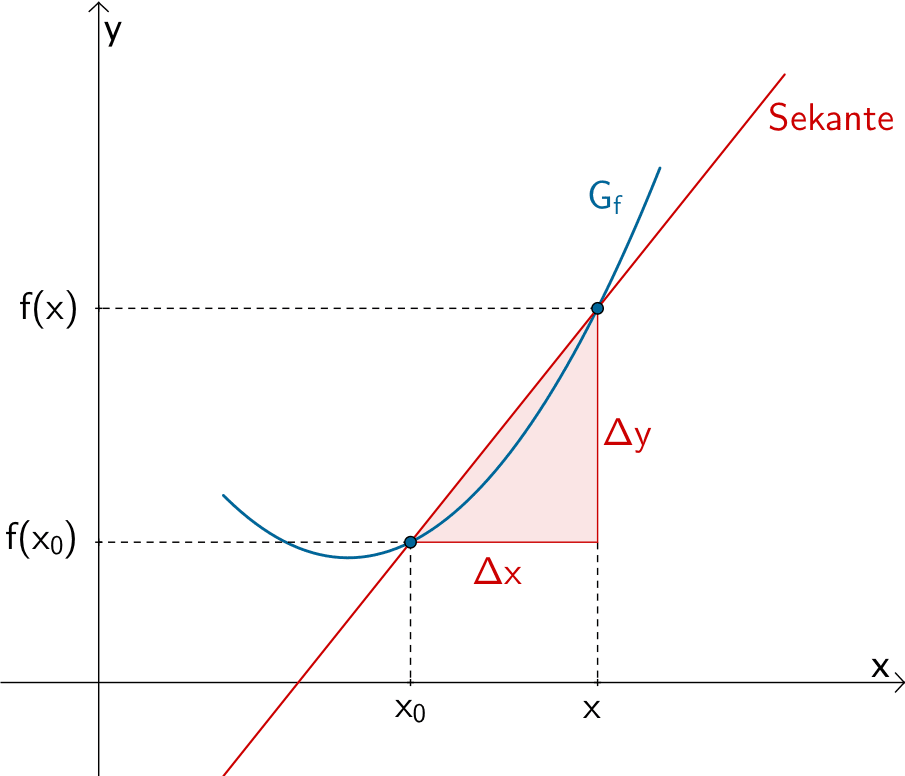
Der Differenzenquotient oder die mittlere Änderungsrate \(m_{s} = \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt die Steigung der Sekante durch den Punkt \((x_{0}|f(x_{0}))\) und einen weiteren Punkt des Graphen der Funktion \(f\).
\[\begin{align*} m_{S} &= \frac{n(2) - n(0)}{2\,\sf{h} - 0\, \sf{h}} \\[0.8em] &= \frac{3 \cdot 2^{2} - 60 \cdot 2 + 500 - (3 \cdot 0^{2} - 60 \cdot 0 + 500)}{2\,\sf{h}} \\[0.8em] &= \frac{12 - 120 + 500 - 500}{2\,\sf{h}} \\[0.8em] &= \frac{-108}{2\,\sf{h}} \\[0.8em] &= -54\,\frac{1}{\sf{h}} \end{align*}\]
Die Anzahl der Pollen in einem Kubikmeter Luft nimmt während der ersten beiden Stunden der Messung durchschnittlich um 54 Pollen pro Stunde ab.
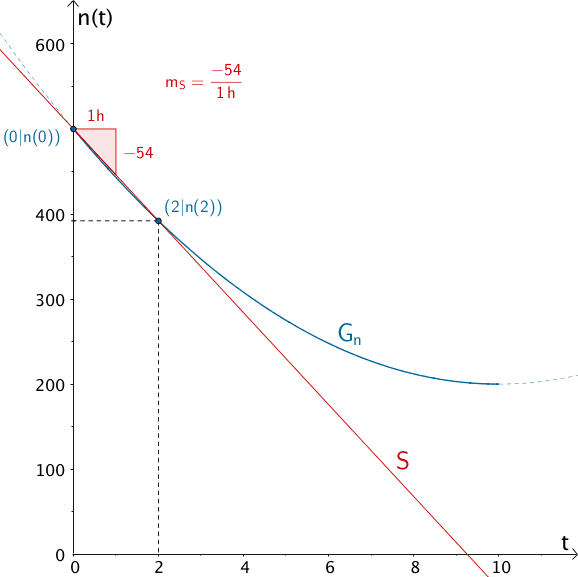
Graphische Veranschaulichung: Die mittleren Änderungsrate der Anzahl der Pollen in einem Kubikmeter Luft während der ersten beiden Stunden der Messung entspricht der Steigung \(m_{S}\) der Sekante \(S\) durch die Punkte \((0|n(0))\) und \((2|n(2))\) des Graphen \(G_{n}\) der Funktion \(n(t)\).


