Der Innenausbau des Pavillons erfordert eine möglichst kurze, dünne Strebe zwischen dem Mittelpunkt der Grundfläche und der südlichen Außenwand. Ermitteln Sie, in welcher Höhe über der Grundfläche die Strebe an der Außenwand befestigt ist.
(5 BE)
Lösung zu Teilaufgabe 1c
1. Lösungsansatz: Lotgerade auf Ebene \(E\)
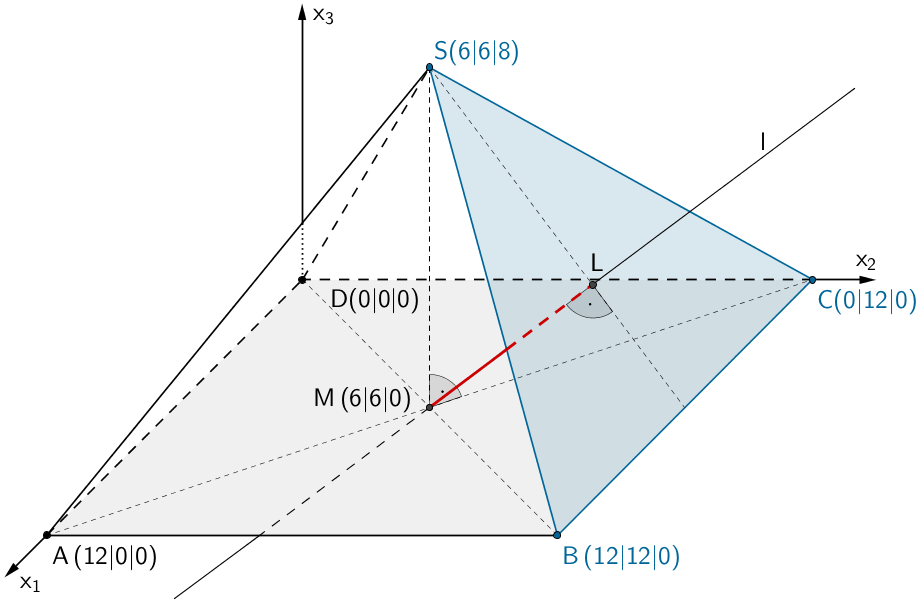
Es sei \(M\) der Mittelpunkt der Grundfläche \(ABCD\). Die Lotgerade \(l\) mit den Eigenschaften \(M \in l\) und \(l \perp E\) schneidet die Ebene \(E\) im Lotfußpunkt \(L\). Die \(x_3\)-Koordinate von \(L\) entspricht der Höhe über der Grundfläche, in der die Strebe (rot) an der Außenwand befestigt ist.
Koordinaten des Mittelpunktes \(M\) berechnen:
Mittelpunkt einer Strecke
Für den Ortsvektor \(\overrightarrow{M}\) des Mittelpunkts \(M\) einer Strecke \([AB]\) gilt:
\[\overrightarrow{M} = \frac{1}{2} \left( \overrightarrow{A} + \overrightarrow{B} \right)\]
\[\overrightarrow{M} = \overrightarrow{M}_{BD} = \frac{1}{2} \cdot \left( \overrightarrow{B} + \overrightarrow{D} \right) = \frac{1}{2} \cdot \left[ \begin{pmatrix} 12 \\ 12 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \right] = \begin{pmatrix} 6 \\ 6 \\ 0 \end{pmatrix}\]
oder
\[\overrightarrow{M} = \overrightarrow{M}_{AC} = \frac{1}{2} \cdot \left( \overrightarrow{A} + \overrightarrow{C} \right) = \frac{1}{2} \cdot \left[ \begin{pmatrix} 12 \\ 0 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 12 \\ 0 \end{pmatrix} \right] = \begin{pmatrix} 6 \\ 6 \\ 0 \end{pmatrix}\]
oder als Alternative:
Die Koordinaten des Mittelpunktes \(M\) lassen sich aus den Koordinaten der Spitze \(S\,(6|6|8)\) ableiten. Da die Pyramide \(ABCDS\) eine gerade Pyramide ist, deren Grundfläche in der \(x_1x_2\)-Ebene liegt, ist der Mittelpunkt \(M\) der Lotfußpunkt des Lotes der Spitze \(S\) auf die \(x_1x_2\)-Ebene. Damit hat \(M\) dieselben \(x_1\)- und \(x_2\)-Koordinaten wie \(S\) und die \(x_3\)-Koordinate ist Null.
\[S\,(6|6|8) \quad \Longrightarrow \quad M\,(6|6|0)\]
Geradengleichung der Lotgeraden \(l\) aufstellen:
Lotgerade auf eine Ebene
\[E\,\colon \overrightarrow{n}_E \circ (\overrightarrow{X} - \overrightarrow{A}) = 0; \quad P\,(p_1|p_2|p_3)\]
Die Lotgerade \(\ell\) mit \(P \in \ell\) auf eine Ebene \(E\) ist durch den Ortsvektor \(\overrightarrow{P}\) und den Normalenvektor \(\overrightarrow{n}_E\) eindeutig bestimmt:
\[\ell\,\colon \overrightarrow{X} = \overrightarrow{P} + \lambda \cdot \overrightarrow{n}_E; \; \lambda \in \mathbb R\]
\[M \in l\,; \quad \overrightarrow{n}_E = \begin{pmatrix} 0 \\ 4 \\ 3 \end{pmatrix}\]
\[\begin{align*} \Longrightarrow \quad l\,\colon\; \overrightarrow{X} &= \overrightarrow{M} + \lambda \cdot \overrightarrow{n}_E & & \lambda \in \mathbb R \\[0.8em] l\,\colon\; \overrightarrow{X} &= \begin{pmatrix} 6 \\ 6 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ 4 \\ 3 \end{pmatrix} \end{align*}\]
\(x_3\)-Koordinate des Lotfußpunktes \(L\) berechnen:
Zur Berechnung des Lotfußpunktes \(L\) setzt man die Koordinaten des Ortsvektors \(\overrightarrow{X}\) aus der Geradengleichung von \(l\) in die Normalengleichung der Ebene \(E\) ein und löst die Gleichung nach dem Parameter \(λ\) auf.
\[l\,\colon\; \overrightarrow{X} = \begin{pmatrix} 6 \\ 6 \\ 0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ 4 \\ 3 \end{pmatrix}\]
\[E\,\colon\; 4x_2 + 3x_3 - 48 = 0\]
\[\begin{align*} l \cap E\,\colon\; 4 \cdot (6 + 4\lambda) + 3 \cdot (0 +3\lambda) - 48 &= 0 \\[0.8em] 24 + 16\lambda + 9\lambda - 48 &= 0 \\[0.8em] -24 + 25\lambda &= 0 & &| + 24 \\[0.8em] 25\lambda &= 24 & &| : 25 \\[0.8em] \lambda &= 0{,}96 \end{align*}\]
Parameterwert \( \lambda = 0{,}96\) in die Geradengleichung von \(l\) einsetzen:
\[L \in l\,\colon\; \overrightarrow{L} = \begin{pmatrix} 6 \\ 6 \\ 0 \end{pmatrix} + 0{,}96 \cdot \begin{pmatrix} 0 \\ 4 \\ 3 \end{pmatrix} = \begin{pmatrix} 6 \\ 9{,}84 \\ 2{,}88 \end{pmatrix}\]
\[\Longrightarrow \quad x_{3_L} = 2{,}88\]
Die Strebe ist an der südlichen Außenwand in einer Höhe von 2,88 m über der Grundfläche befestigt.
2. Lösungsansatz: Trigonometrische Beziehung im rechtwinkligen Dreieck
![Lotfußpunkt L des Lotes des Punktes M auf die Ebene E, Mittelpunkt N der Strecke [BC], Lotfußpunkt F des Lotes des Punktes L auf die x₁x₂-Ebene, rechtwinklige Dreiecke MNL und FNL, Maß φ des Winkels ∠ LNF bzw. LNM](/images/stories/B2013_G_II/B2013_G_II_1c_02.png "Lotfußpunkt L des Lotes des Punktes M auf die Ebene E, Mittelpunkt N der Strecke [BC], Lotfußpunkt F des Lotes des Punktes L auf die x₁x₂-Ebene, rechtwinklige Dreiecke MNL und FNL, Maß φ des Winkels ∠ LNF bzw. LNM")
Rechtwinklige Dreiecke \(MNL\) und \(FNL\), Maß \(\varphi\) des Winkles \(\measuredangle LNF\) bzw. \(\measuredangle LNM\)
Die Länge der Strecke \([LF]\) entspricht der Höhe über der Grundfläche, in der die Strebe (rot) an der Außenwand befestigt ist.
Trigonometrische Betrachtung der rechtwinkligen Dreiecke \(MNL\) und \(FNL\):
Trigonometrische Beziehungen im rechtwinkligen Dreieck (vgl. Merkhilfe)
\[\sin \alpha = \frac{\text{Gegenkathete}}{\text{Hypotenuse}}\]
\[\cos \alpha = \frac{\text{Ankathete}}{\text{Hypotenuse}}\]
\[\tan \alpha = \frac{\text{Gegenkathete}}{\text{Ankathete}}\]
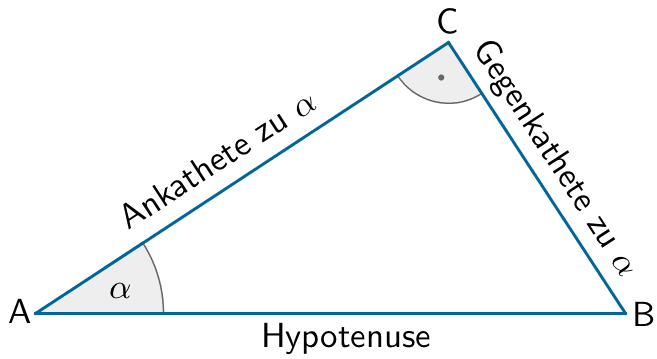
\[\sin \varphi = \frac{\overline{LM}}{\overline{MN}}\,; \quad \sin \varphi = \frac{\overline{LF}}{\overline{NL}}\]
\[\Longrightarrow \quad \frac{\overline{LF}}{\overline{NL}} = \frac{\overline{LM}}{\overline{MN}} \quad \Longleftrightarrow \quad \overline{LF} = \frac{\overline{LM} \cdot \overline{NL}}{\overline{MN}}\]
Länge der Strecke \([MN]\) berechnen:
\(\displaystyle \overline{MN} = \frac{1}{2} \cdot \overline{AB} = \frac{1}{2} \cdot 12 = 6 \;\) (siehe Angabe Teilaufgabe 1a)
Länge der Strecke \([LM]\) berechnen:
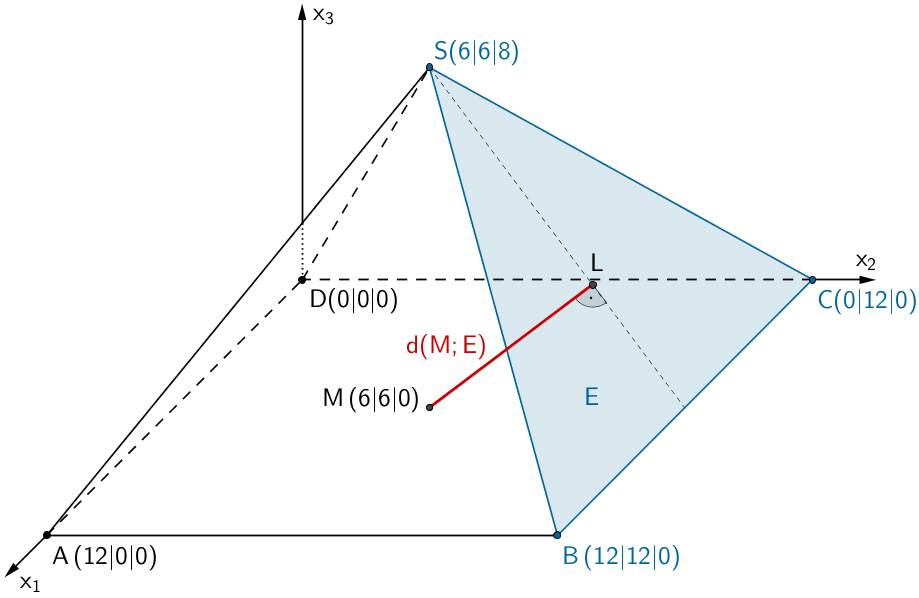
Abstand \(d\,(M;E)\) des Punktes \(M\) von der Ebene \(E\) (siehe Teilaufgabe 1b)
Die Länge der Strecke \([LM]\) entspricht dem Abstand des Punktes \(M\) von der Ebene \(E\).
Abstand eines Punktes von einer Ebene
Für den Abstand \(d(P;E)\) eines Punktes \(P(p_{1}|p_{2}|p_{3})\) zu einer in der Hesseschen Normalenform (HNF) vorliegenden Ebene \(E\) gilt:
Vektordarstellung
\[E \colon \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{P} - \overrightarrow{A}) \right|\]
Koordinatendarstellung
\[E \colon \frac{n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \frac{n_{1}p_{1} + n_{2}p_{2} + n_{3}p_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} \right|\]
Dabei ist \(\overrightarrow{n}^{0}_{E} = \dfrac{\overrightarrow{n}_{E}}{\vert \overrightarrow{n}_{E} \vert}\) der Einheitsvektor des Normalenvektors \(\overrightarrow{n}_{E}\) der Ebene \(E\).
\[M\,(6|6|0)\]
\(E\,\colon\: 4x_2 + 3x_3 - 48 = 0\)
\[\vert \overrightarrow{n}_E \vert = \left| \begin{pmatrix} 4 \\ 0 \\ 3 \end{pmatrix} \right| = \sqrt{4^2 + 0^2 + 3^2} = \sqrt{25} = 5\]
\[\begin{align*}\overline{LM} &= d\,(M;E) \\[0.8em] &= \frac{\vert 4m_1 + 3m_3 - 48 \vert}{\vert \overrightarrow{n}_E \vert} \\[0.8em] &= \frac{\vert 4 \cdot 6 + 3 \cdot 0 - 48 \vert}{5} \\[0.8em] &= \frac{24}{5} = 4{,}8 \end{align*}\]
Länge der Strecke \([NL]\) berechnen:
Die Länge der Strecke \([NL]\) lässt sich mithilfe des Satzes des Pythagoras berechnen.
Satzgruppe des Pythagoras im rechtwinkligen Dreieck
Satz des Pythagoras
\[\hspace{5px}a^2 + b^2 = c^2\]
Höhensatz
\[h^2 = p \cdot q\]
Kathetensatz
\[a^2 = c \cdot p\,; \enspace b^2 = c \cdot q\]
\[\begin{align*} {\overline{LM}}^2 + {\overline{NL}}^2 &= {\overline{MN}}^2 \\[0.8em] {\overline{NL}}^2 &= {\overline{MN}}^2 - {\overline{LM}}^2 & &| \; \sqrt{\quad} \\[0.8em] \overline{NL} &= \sqrt{{\overline{MN}}^2 - {\overline{LM}}^2} \\[0.8em] &= \sqrt{6^2 - 4{,}8^2} \\[0.8em] &= 3{,}6 \end{align*}\]
Länge der Strecke \([LF]\) berechnen:
\[\overline{LF} = \frac{\overline{LM} \cdot \overline{NL}}{\overline{MN}} = \frac{4{,}8 \cdot 3{,}6}{6} = 2{,}88\]
Die Strebe ist an der südlichen Außenwand in einer Höhe von 2,88 m über der Grundfläche befestigt.
