Begründen Sie, dass \(\lim \limits_{x\,\to\,0}f'(x) = -\infty\) und \(\lim \limits_{x\,\to\,+\infty}f'(x) = 0\) gilt. Geben Sie \(f'(0{,}5)\) und \(f'(10)\) auf eine Dezimale genau an und zeichnen Sie den Graphen der Ableitungsfunktion \(f'\) unter Berücksichtigung aller bisherigen Ergebnisse in Abbildung 1 ein.

(6 BE)

Lösung zu Teilaufgabe 1c

 

\(f'(x) = \frac{4}{x} \cdot \ln{x}; \; D_{f'} = \mathbb R^{+}\) (vgl. Teilaufgabe 1a)

 

Begründung, dass \(\lim \limits_{x\,\to\,0}f'(x) = -\infty\) und \(\lim \limits_{x\,\to\,+\infty}f'(x) = 0\) gilt

 

\[\lim \limits_{x\,\to\,0} f'(x) = \lim \limits_{x\,\to\,0} \underbrace{\frac{4}{x}}_{\large \to \, +\infty} \cdot \underbrace{\ln{x}}_{\large \to \, -\infty} = -\infty \]

 

Mit \(D = \mathbb R^{+}\) besitzt \(G_{f}\) die \(y\)-Achse als senkrechte Asymptote und fällt für \(x \to 0\) unendlich steil.

 

\[\lim \limits_{x\,\to\,+\infty} f'(x) = \lim \limits_{x\,\to\,+\infty} \underbrace{\frac{4}{x}}_{\large \to \,0} \cdot \underbrace{\ln{x}}_{\large\to\,\,+\infty} = 4 \cdot \underbrace{\lim \limits_{x\,\to\,+\infty}\frac{\ln{x}}{x} = 0}_{\large \text{vgl. Merkhilfe}}\]

 

Für \(x \to +\infty\) geht \(\ln{x}\) langsamer gegen \(+\infty\) als \(\dfrac{4}{x}\) gegen \(0\).

 

Funktionswerte \(f'(0{,}5)\) und \(f'(10)\) auf eine Dezimale genau

 

\[f'(0{,}5) = \frac{4}{0{,}5} \cdot \ln{0{,}5} \approx -5{,}5\]

\[f'(10) = \frac{4}{10} \cdot \ln{10} \approx 0{,}9\]

 

Zeichnung des Graphen der Ableitungsfunktion \(f'\)

Für die Zeichnung des Graphen der Ableitungsfunktion \(f'\) sind folgende bisherige Ergebnisse von Bedeutung:

  • \(G_{f}\) besitzt den Tiefpunkt \(T(1|-2)\) (vgl. Teilaufgabe 1a)
  • \(G_{f}\) besitzt den Wendepunkt \(W(e|0)\) (vgl. Teilaufgabe 1b)
  • \(\lim \limits_{x\,\to\,0} f'(x) = -\infty\) und \(\lim \limits_{x\,\to\,+\infty} f'(x) = 0\) (vgl. oben)
  • \(f'(0{,}5) \approx -5{,}5\) und \(f'(10) \approx -0{,}9\) (vgl. oben)
Graph der Ableitungsfunktion f'

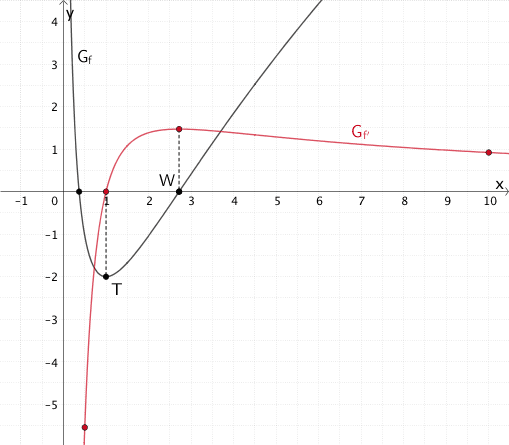
Erläuterung (nicht verlangt):

Im Tiefpunkt \(T(1|-2)\) besitzt \(G_{f}\) eine waagrechte Tangente mit der Steigung Null. Also hat \(G_{f'}\) die Nullstelle \(x = 1\).

Im Wendepunkt \(W(e|0)\) ist die Steigung von \(G_{f}\) maximal. Also besitzt \(G_{f'}\) an der Stelle \(x = e\) einen Hochpunkt.