Bestimmen Sie rechnerisch Lage und Art der Extrempunkte von \(G_f\,\).
(8 BE)
Lösung zu Teilaufgabe 1b
\[f(x) = \frac{1}{2}x - \frac{1}{2} + \frac{8}{x + 1}\,; \quad D = \mathbb R \, \backslash \, \{-1\}\]
Lage der Extrempunkte von \(G_f\)
Notwendige Bedingung für Extremstellen:
\[f'(x) \overset{!}{=} 0\]
Erste Ableitung \(f'(x)\) bilden:
Quotientenregel
\[ f(x) = \frac{u(x)}{v(x)} \quad \Longrightarrow \quad f'(x) = \frac{u'(x) \cdot v(x) - u(x) \cdot v'(x)}{[v(x)]^2}\]
Ableitung einer Potenzfunktionen
\[ f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[\begin{align*} f'(x) &= \frac{1}{2} + \frac{0 \cdot (x + 1) - 8 \cdot 1}{(x + 1)^2} \\[0.8em] &= \frac{1}{2} - \frac{8}{(x + 1)^2} \end{align*}\]
\[\begin{align*}f'(x) \overset{!}{=} 0 \quad \Longrightarrow \quad \frac{1}{2} - \frac{8}{(x + 1)^2} &= 0 \\[0.8em] \frac{1}{2} &= \frac{8}{(x + 1)^2} \\[0.8em] (x + 1)^2 &= 16 & &| \;\sqrt{\quad} \\[0.8em] x + 1 &= \pm4 & &| -1 \\[0.8em] x_1 = -5 \enspace &\vee \enspace x_2 = 3 \end{align*}\]
\(\Longrightarrow \quad x_{E_1} = -5\) und \(x_{E_2} = 3\) sind Extremstellen von \(G_f\).
\[f(-5) = \frac{1}{2} \cdot (-5) - \frac{1}{2} + \frac{8}{(-5) + 1} = -5\]
\[f(3) = \frac{1}{2} \cdot 3 - \frac{1}{2} + \frac{8}{3 + 1} = 3\]
\(\Longrightarrow \quad (-5|-5)\) und \((3|3)\) sind Extrempunkte von \(G_f\).
Art der Extrempunkte von \(G_f\)
1. Lösungsansatz: Vorzeichenwechsel von \(f'(x)\) (Monotonieverhalten von \(G_f\))
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Für die Beurteilung des Vorzeichenwechsels von \(f'(x)\) ist zweckmäßig, den Funktionsterm umzuformen.
\[\begin{align*}f'(x) &= \frac{1}{2} - \frac{8}{(x + 1)^2} \\[0.8em] &= \frac{(x + 1)^2 - 16}{2(x + 1)^2} \\[0.8em] &= \frac{x^2 + 2x - 15}{2(x + 1)^2} \end{align*}\]
Die Nullstellen von \(f'(x)\) sind mit \(x = -5\) und \(x = 3\) bereits bekannt. Damit lässt sich der Zähler von \(f'(x)\) als Produkt seiner Linearfaktoren angeben.
\[f'(x) = \frac{(x + 5) \cdot (x - 3)}{\underbrace{2(x + 1)^2}_{> \, 0}}\]
Das Produkt des Zählers bestimmt das Vorzeichen von \(f'(x)\) in der Nähe der Extremstellen \(x_{E_1} = -5\) und \(x_{E_2} = 3\) und somit das Monotonieverhalten von \(G_f\) in der Umgebung der Extremstellen.
\[x_{E_1} = -5\]
\[\left. \begin{align*} &f'(x) > 0 \enspace \text{für} \enspace x \in \; ]-\infty;-5[ \\ &f'(-5) = 0 \\ &f'(x) < 0 \enspace \text{für} \enspace x \in \; ]-5;-1[ \end{align*} \right\} \enspace \Rightarrow \enspace \text{Hochpunkt}, \; HoP \, (-5|-5)\]
\[x_{E_2} = 3\]
\[\left. \begin{align*} &f'(x) < 0 \enspace \text{für} \enspace x \in \; ]-1;3[ \\ &f'(3) = 0 \\ &f'(x) > 0 \enspace \text{für} \enspace x \in \; ]3;+\infty[ \end{align*} \right\} \enspace \Rightarrow \enspace \text{Tiefpunkt}, \; TiP \, (3|3)\]
Als Alternative (ohne Umformen des Funktionsterms von f'(x)) betrachtet man die Ungleichungen \(f'(x) > 0\) und \(f'(x) < 0\).
\[\begin{align*} f'(x) &> 0 \\[0.8em] \frac{1}{2} - \frac{8}{(x + 1)^2} &> 0 \\[0.8em] \frac{1}{2} &> \frac{8}{(x + 1)^2} \\[0.8em] (x +1)^2 &> 16 & &| \;\sqrt{\quad} \\[0.8em] x + 1 > 4 \enspace &\vee \enspace x + 1 < -4 \\[0.8em] x > 3 \enspace &\vee \enspace x < -5 \end{align*}\]
\[\Longrightarrow \quad x \in ]-\infty; -5[\; \cup \; ]3; +\infty[\]
\[\begin{align*} f'(x) &< 0 \\[0.8em] \frac{1}{2} - \frac{8}{(x + 1)^2} &< 0 \\[0.8em] \frac{1}{2} &< \frac{8}{(x + 1)^2} \\[0.8em] (x +1)^2 &< 16 & &| \;\sqrt{\quad} \\[0.8em] x + 1 < 4 \enspace &\vee \enspace x + 1 > -4 \\[0.8em] x < 3 \enspace &\vee \enspace x > -5 \end{align*}\]
\[\begin{align*}\Longrightarrow \quad x &\in ]-5; 3[ \; \backslash \; \{-1\} \\[0.8em] x &\in ]-5; -1[ \; \cup \; ]-1; 3[\end{align*}\]
\[x_{E_1} = -5\]
\[\left. \begin{align*} &f'(x) > 0 \enspace \text{für} \enspace x \in \; ]-\infty;-5[ \\ &f'(-5) = 0 \\ &f'(x) < 0 \enspace \text{für} \enspace x \in \; ]-5;-1[ \end{align*} \right\} \enspace \Rightarrow \enspace \text{Hochpunkt}, \; HoP \, (-5|-5)\]
\[x_{E_2} = 3\]
\[\left. \begin{align*} &f'(x) < 0 \enspace \text{für} \enspace x \in \; ]-1;3[ \\ &f'(3) = 0 \\ &f'(x) > 0 \enspace \text{für} \enspace x \in \; ]3;+\infty[ \end{align*} \right\} \enspace \Rightarrow \enspace \text{Tiefpunkt}, \; TiP \, (3|3)\]
2. Lösungsansatz: Art der Extrema mit Hilfe der zweiten Ableitung
Anwendung der Differentialrechnung:
Art von Extrempunkten mithilfe der zweiten Ableitung nachweisen
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) > 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Minimum (Tiefpunkt).
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) < 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Maximum (Hochpunkt).
Zweite Ableitung \(f''(x)\) bilden:
Quotientenregel
\[ f(x) = \frac{u(x)}{v(x)} \quad \Longrightarrow \quad f'(x) = \frac{u'(x) \cdot v(x) - u(x) \cdot v'(x)}{[v(x)]^2}\]
Kettenregel
\[ f(x) = u(v(x)) \quad \Longrightarrow \quad f'(x) = u'(v(x)) \cdot v'(x) \]
Ableitung einer Potenzfunktion
\[ f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[f'(x) = \frac{1}{2} - \frac{8}{(x + 1)^2}\,; \quad D = \mathbb R \, \backslash \, \{-1\}\]
\[\begin{align*} f''(x) &= 0 - \frac{0 \cdot (x + 1)^2 - 8 \cdot 2(x + 1) \cdot 1}{\left[(x + 1)^2\right]^2} \\[0.8em] &= \frac{16(x + 1)}{(x + 1)^4} \\[0.8em] &= \frac{16}{(x + 1)^3} \end{align*}\]
\[x_{E_1} = -5\]
\[f''(-5) = \frac{16}{(-5 + 1)^3} = \frac{16}{-64} = -\frac{1}{4}\]
\[\left. \begin{align*} &f'(-5) = 0 \\ &f''(-5) < 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Hochpunkt}, \; HoP\,(-5|-5)\]
\[x_{E_2} = 3\]
\[f''(3) = \frac{16}{(3 + 1)^3} = \frac{16}{64} = \frac{1}{4}\]
\[\left. \begin{align*} &f'(3) = 0 \\ &f''(3) > 0 \end{align*} \right\} \enspace \Rightarrow \enspace \text{Tiefpunkt}, \; TiP\,(3|3)\]
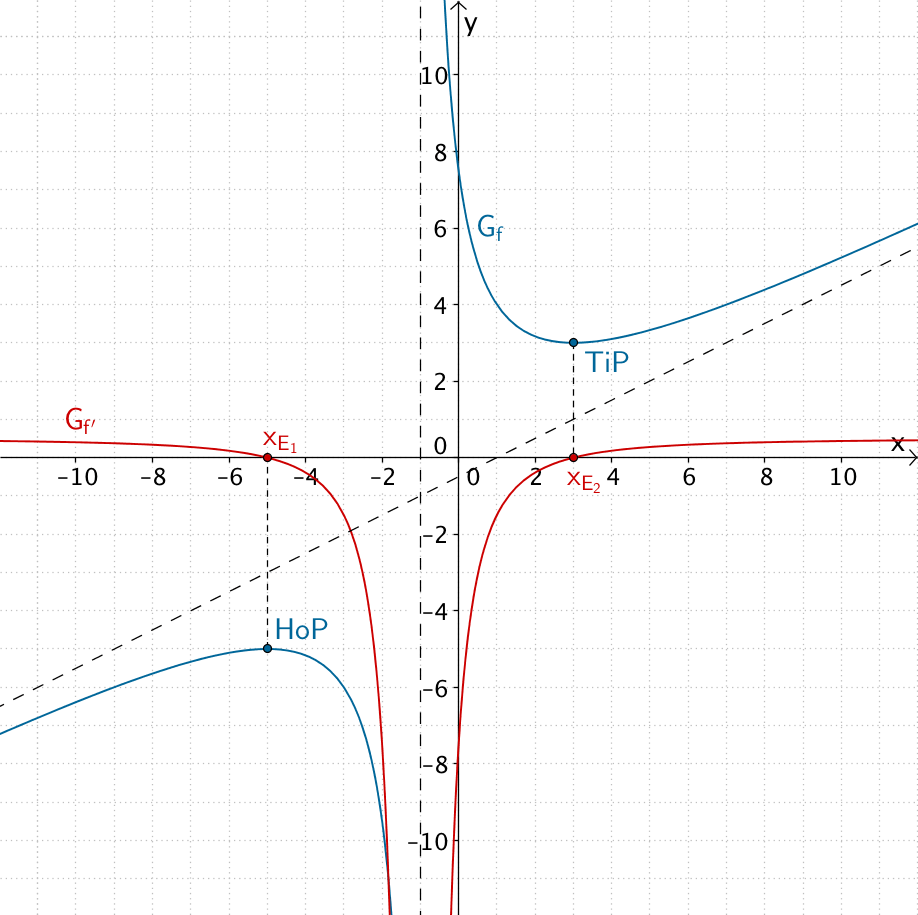
Graph von \(f\) und Graph von \(f'\)


