Der Graph von \(f\) wird verschoben. Der Punkt \((2|0)\) des Graphen der Funktion \(f\) besitzt nach der Verschiebung die Koordinaten \((3|2)\). Der verschobene Graph gehört zu einer Funktion \(h\). Geben Sie eine Gleichung von \(h\) an.
(2 BE)
Lösung zu Teilaufgabe 2b
Verschieben eines Funktionsgraphen
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
\[f(x) = x^{3} - 6x^{2} + 11x - 6\,; \enspace x \in \mathbb R\]
Der Graph der Funktiom \(f\) wird um 1 in \(x\)-Richtung und um \(2\) in \(y\)-Richtung verschoben.
\[\begin{align*} h(x) &= f(x - 1) + 2 \\[0.8em] &= (x - 1)^{3} - 6 \cdot (x - 1)^{2} + 11 \cdot (x - 1) - 6 + 2 \\[0.8em] &= (x - 1)^{3} - 6 \cdot (x - 1)^{2} + 11 \cdot (x - 1) - 4 \end{align*}\]
Anmerkung: Die Aufgabenstellung verlangt nach einer Gleichung von \(h\). Es ist nicht notwendig, den Term auszumultiplizieren und zusammenzufassen, um ihn in die Form \(ax^{3} + bx^{2} + cx + d\) zu bringen.
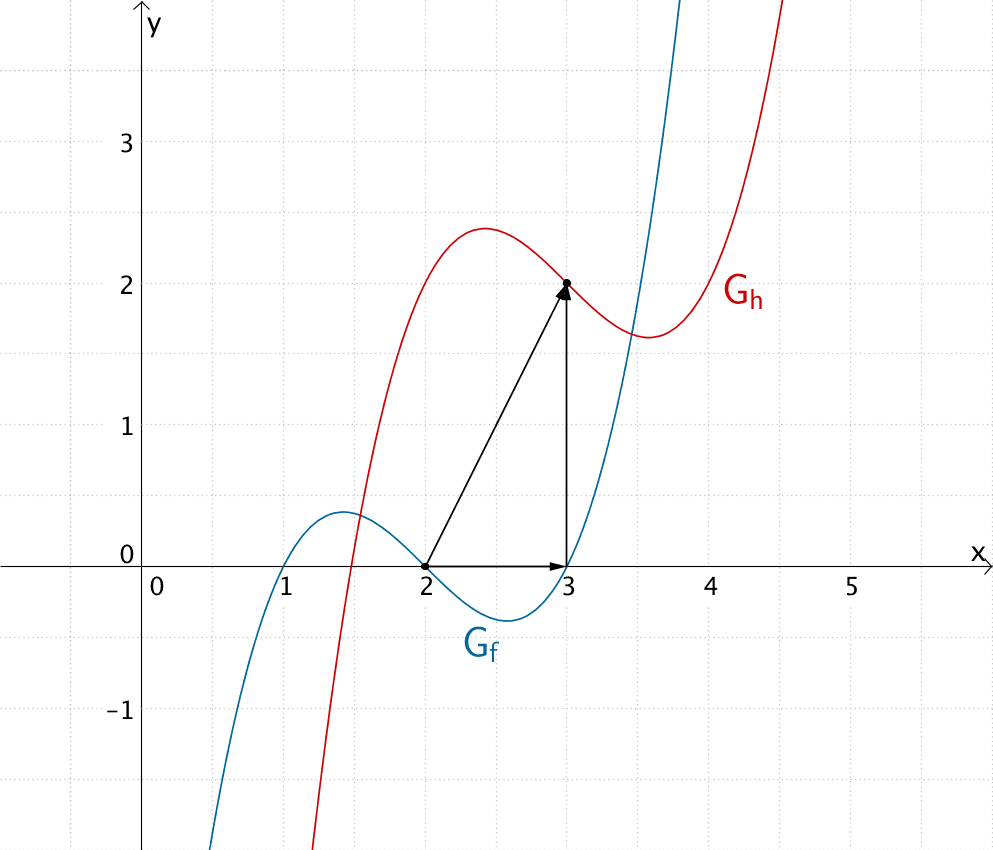
Verschiebung von \(G_{f}\) um 1 in \(x\)-Richtung und 2 in \(y\)-Richtung


