Berechnen Sie die Steigung der Tangente \(g\) an \(G_{f}\) im Punkt \(P(2|f(2))\) auf eine Dezimale genau. Zeichnen Sie den Punkt \(P\) und die Gerade \(g\) in ein Koordinatensystem ein (Platzbedarf im Hinblick auf das Folgende: \(-4 \leq x \leq 4\), \(-1 \leq y \leq 9\)).
(3 BE)
Lösung zu Teilaufgabe 1e
Tangentensteigung
Steigung der Tangente \(g\) an \(G_{f}\) im Punkt \(P(2|f(2))\)
\[f(x) = e^{\frac{1}{2}x} + e^{-\frac{1}{2}x}; \; D = \mathbb R\]
\[P(2|f(2))\]
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[m_{g} = f'(2)\]
Aus Teilaufgabe 1c ist bekannt:
\[f'(x) = \frac{1}{2} \cdot \left( e^{\frac{1}{2}x} - e^{-\frac{1}{2}x} \right)\]
\[\begin{align*}m_{g} &= f'(2) \\[0.8em] &= \frac{1}{2} \cdot \left( e^{\frac{1}{2} \cdot 2} - e^{-\frac{1}{2} \cdot 2} \right) \\[0.8em] &= \frac{1}{2} \cdot \left( e - e^{-1} \right) \\[0.8em] &\approx 1{,}2 \end{align*}\]
Einzeichnen des Punktes \(P\) und der Geraden \(g\) in ein Koordinatensystem
\[f(x) = e^{\frac{1}{2}x} + e^{-\frac{1}{2}x}; \; D = \mathbb R\]
\[P(2|f(2))\]
\[f(2) = e^{\frac{1}{2} \cdot 2} + e^{\frac{1}{2} \cdot 2} = e + e^{-1} \approx 3{,}1\]
\[\Longrightarrow \quad P(2|3{,}1)\]
Um die Tangente \(g\) an \(G_{f}\) im Punkt \(P\) zu zeichnen, wählt man entweder ausgehend vom Punkt \(P\) ein der Tangentensteigung \(m_{g}\) entsprechendes Steigungsdreieck, oder man ermittelt die vollständige Gleichung der Tangente \(g\).
Im Falle eines Steigungsdreiecks, ist es sinnvoll, die Tangentensteigung als ganzahligen Bruch anzugeben: \(m_{g} = 1{,}2 = \frac{6}{5}\). Das Steigungsdreieck wird damit genauer.
Ermittelt man die Tangentengleichung \(g \colon y = 1{,}2x + t\), erhält man mit dem \(y\)-Achsenabschnitt \(t\) einen weiteren Punkt, um die Tangente \(g\) möglichst exakt in das Koordinatensystem einzeichnen zu können.
Ermitteln der Tangentengleichung (optional):
\[\begin{align*} g \colon y &= 1{,}2x + t \\[0.8em] P(2|3{,}1) \in g \colon 3{,}1 &= 1{,}2 \cdot 2 + t \\[0.8em] 3{,}1 &= 2{,}4 + t & &| - 2{,}4 \\[0.8em] 0{,}7 &= t \end{align*}\]
\[\Longrightarrow \quad g \colon y = 1{,}2x + 0{,}7\]
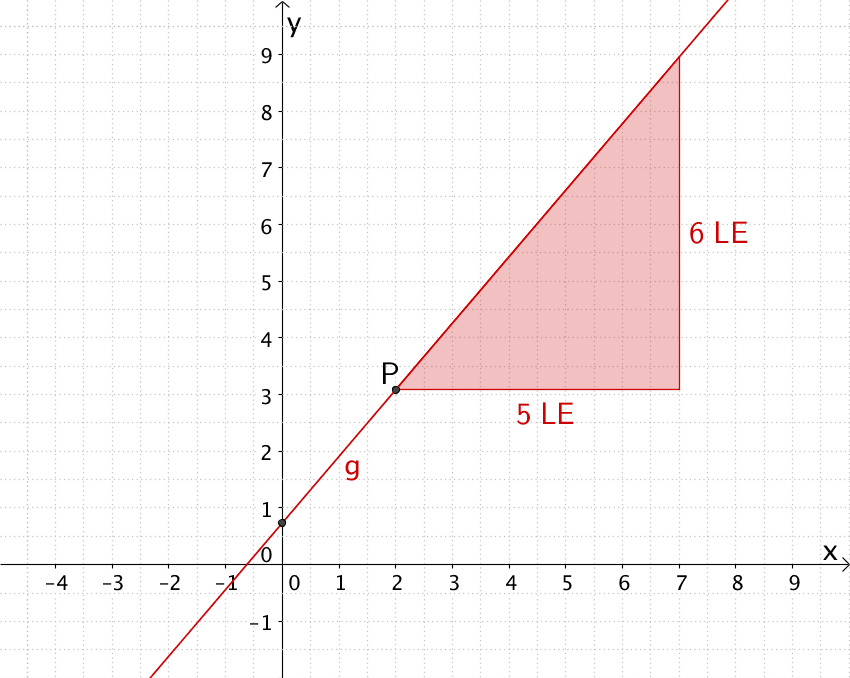
Punkt \(P\) und Gerade \(g\) (Tangente an \(G_{f}\) im Punkt \(P\)) mit Steigungsdreieck


