Interpretieren Sie den folgenden Sachverhalt geometrisch:
Für jede Stammfunktion \(F\) von \(f\) und für jede reelle Zahl \(w > 2022\) gilt
\[F(w) - F(0) \approx \int_0^{2022} f(x)dx\]
(3 BE)
Lösung zu Teilaufgabe 1e
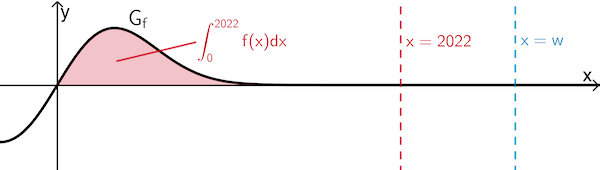
Skizze schematisch (nicht verlangt): Das bestimmte Integral \(\displaystyle \textcolor{#cc071e}{\int_0^{2022}f(x)dx}\) lässt sich geometrisch als Flächeninhalt des Flächenstücks interpretieren, das \(G_f\), die \(x\)-Achse und die Gerade mit der Gleichung \(\textcolor{#cc071e}{x = 2022}\) einschließen (vgl. Abiturskript - 1.6.3 Bestimmtes Integral).
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
Somit lautet eine geometrische Interpretation des Sachverhalts
\( \displaystyle \textcolor{#0087c1}{F(w) - F(0)} \approx \textcolor{#cc071e}{\int_0^{2022} f(x)dx} \enspace \Leftrightarrow \enspace \textcolor{#0087c1}{\int_0^w f(x)dx} \approx \textcolor{#cc071e}{\int_0^{2022} f(x)dx}\) mit \(w > 2022\)
beispielsweise wie folgt:
Der Flächeninhalt des Flächenstücks, das \(G_f\), die \(x\)-Achse und die Gerade mit der Gleichung \(\textcolor{#0087c1}{x = w}\) mit \(w > 2022\) einschließen, ist näherungsweise gleich dem Flächeninhalt des Flächenstücks, das \(G_f\), die \(x\)-Achse und die Gerade mit der Gleichung \(\textcolor{#cc071e}{x = 2022}\) einschließen.


