Abbildung 1 zeigt den Graphen der in \(\mathbb R\) definierten Funktion \(p \colon x \mapsto 0{,}5 \cdot (x + 2)^2 - 0{,}5\), die die Nullstellen \(x = -3\) und \(x = -1\) hat.
Für \(x \in D_{f}\) gilt \(\displaystyle f(x) = \frac{1}{p(x)}\).
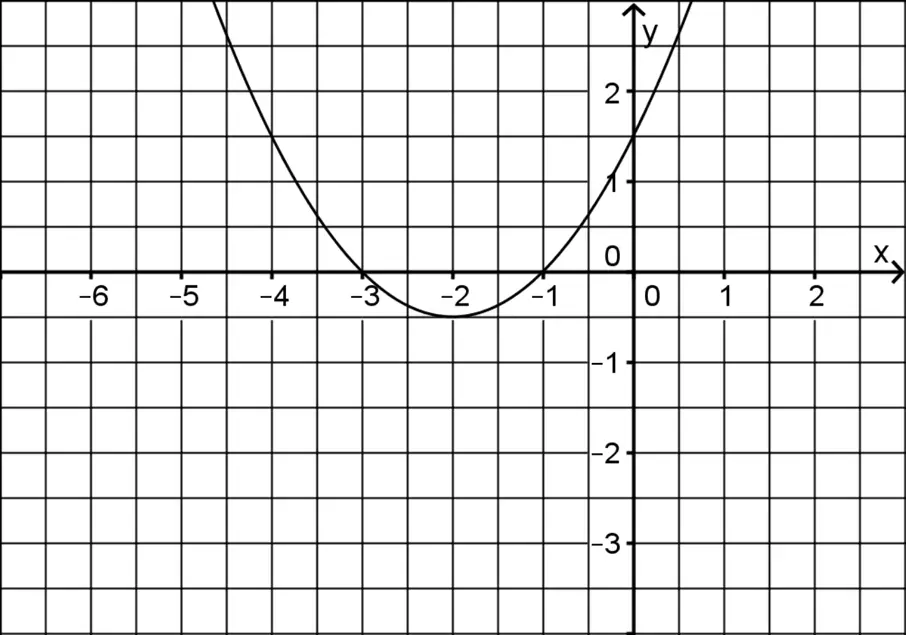Abb. 1
Gemäß der Quotientenregel gilt für die Ableitung \(f'\) und \(p'\) die Beziehung \(\displaystyle f'(x) = -\frac{p'(x)}{\big( p(x) \big)^2}\) für \(x \in D_{f}\).
Zeigen Sie unter Verwendung dieser Beziehung und ohne Berechnung von \(f'(x)\) und \(p'(x)\), dass \(x = -2\) einzige Nullstelle von \(f'\) ist und dass \(G_{f}\) in \(]-3;-2[\) streng monoton steigend sowie in \(]-2;1[\) streng monoton fallend ist. Geben Sie Lage und Art des Extrempunkts von \(G_{f}\) an.
(5 BE)
Lösung zu Teilaufgabe 1c
Nachweis von Nullstelle, Monotonie und Extrempunkt mithilfe eines Funktionsterms/Funktionsgraphen
\[f(x) = \frac{1}{0{,}5 \cdot (x + 2)^{2} - 0{,}5}\,; \enspace D_{f} = \mathbb R \, \backslash \, \{-3;-1\}\]
\[p(x) = 0{,}5 \cdot (x + 2)^{2} - 0{,}5\,; \enspace D =\mathbb R\]
\[f(x) = \frac{1}{p(x)}\,; \enspace x \in D_{f}\]
\[f'(x) = - \frac{p'(x)}{\big(p(x) \big)^{2}}\,; \enspace x \in D_{f}\]
Nachweiß, dass \(x = -2\) einzige Nullstelle von \(f'\) ist
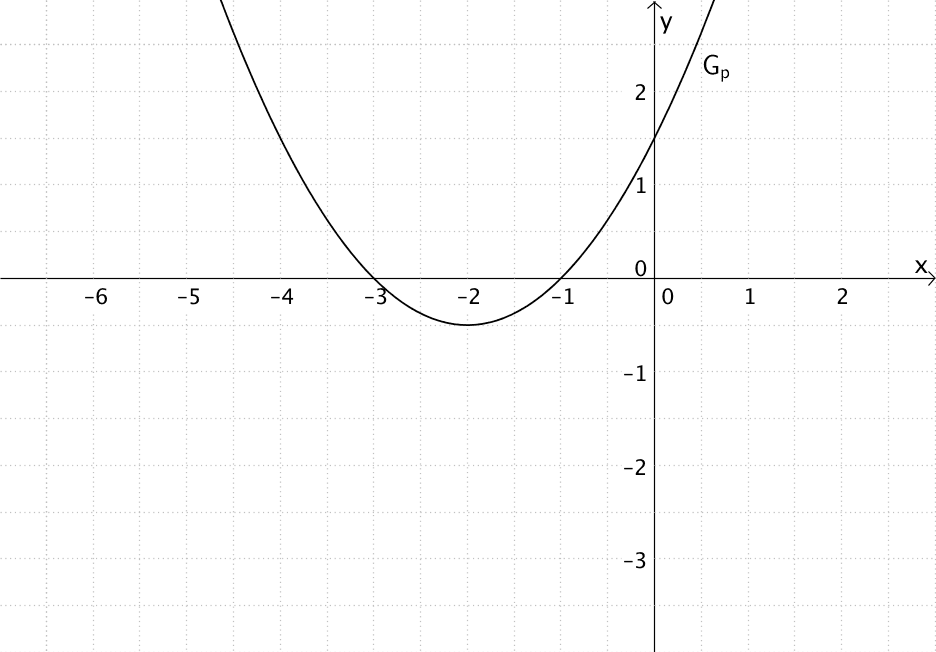Abb. 1
Abbildung 1 zeigt, dass der Graph der quadratischen Funktion \(p\) an der Stelle \(x = -2\) einen Tiefpunkt besitzt. Da der Graph einer quadratischen Funktion genau einen Extrempunkt (Scheitelpunkt) hat, ist der Tiefpunkt an der Stelle \(x = -2\) einziger Extrempunkt von \(G_{p}\).
Der Scheitelpunkt kann auch direkt von dem Funktionsterms von \(p\) abgelesen werden, da dieser in der Scheitelpunktform vorliegt.
Quadratische Funktion:
\[f(x) = ax^2 + bx + c\,; \quad a, b, c \, \in \, \mathbb R\,, a \neq 0\]
Scheitelpunktform
\[f(x) = a(x - d)^2 + e\]
Scheitelpunkt
\[S\,(d|e) \qquad d = -\frac{b}{2a}\,; \quad e = c - \frac{b^2}{4a}\]
\[p(x) = 0{,}5 \cdot (x + 2)^{2} -0{,}5 \quad \Longrightarrow \quad S\,(-2|-0{,}5)\]
Da \(G_{p}\) an der (einzigen) Extremstelle \(x = -2\) eine waagrechte Tangente besitzt, gilt: \(p'(-2) = 0\).
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[\Longrightarrow \quad f'(-2) = -\frac{p'(-2)}{\big( p(-2) \big)^{2}} = \frac{0}{\big( p(-2) \big)^{2}} = 0\]
Somit ist \(x = -2\) einzige Nullstelle von \(f'\).
Nachweiß des Monotonieverhaltens von \(G_{f}\)
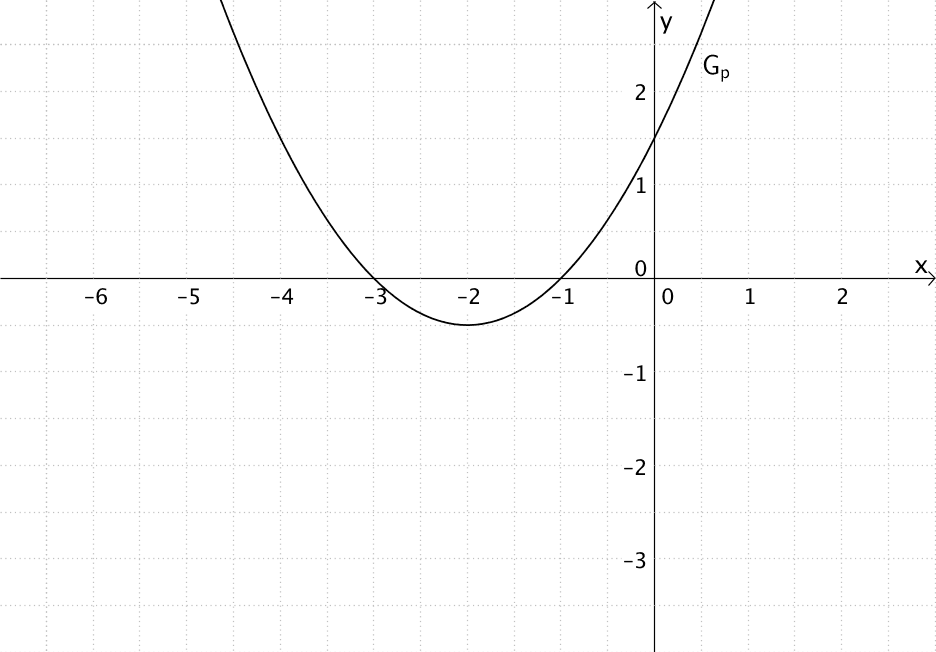Abb. 1
Gemäß Abbildung 1 gilt:
\(G_{p}\) ist in \(]-3;-2[\) streng monoton fallend.
\(G_{p}\) ist in \(]-2;-1[\) streng monoton steigend.
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\(\Longrightarrow \quad p'(x) < 0\) für \(x \in \; ]-3;-2[\)
\(\Longrightarrow \quad p'(x) > 0\) für \(x \in \; ]-2;-1[\)
Mit \(\displaystyle f'(x) = - \frac{p'(x)}{\big(p(x) \big)^{2}}\) folgt daraus:
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\(f'(x) > 0\) für \(x \in \; ]-3;-2[\)
\(\Longrightarrow \quad G_{f}\) ist in \(]-3;-2[\) streng monoton steigend.
\(f'(x) < 0\) für \(x \in \; ]-2;-1[\)
\(\Longrightarrow \quad G_{f}\) ist in \(]-2;-1[\) streng monoton fallend.
Lage und Art des Extrempunkts von \(G_{f}\)
Gemäß Angabe und Nachweis (siehe oben) gilt: \(f'(-2) = 0\). Damit ist die notwendige Bedingung für eine Extremum von \(G_{f}\) an der Stelle \(x = -2\) erfüllt. Da zudem \(G_{f}\) in der Umgebung von \(x = -2\) das Monotonieverhalten von streng monoton steigend zu streng monoton fallend ändert bzw, \(f'\) das Vorzeichen von Plus nach Minus wechselt (hinreichende Bedingung), besitzt \(G_{f}\) an der Stelle \(x = -2\) ein relatives Maximum (einen Hochpunkt).
Anwendung der Differetialrechnung:
Monotoniekriterium
\(\textcolor{#cc071e}{f'(x) < 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) fällt streng monoton in \(I\)
\(\textcolor{#0087c1}{f'(x) > 0}\) im Intervall \( I \; \Rightarrow \; G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
\[\left. \begin{align*} &f'(x) > 0 \enspace \text{für} \; x \in \; ]-3;-2[ \\ &f'(x) = 0 \enspace \text{für} \; x = -2 \\ &f'(x) < 0 \enspace \text{für} \; x \in \; ]-2;-1[ \end{align*} \right\} \enspace \Rightarrow \enspace \text{Hochpunkt}, HoP \,(-2|f(-2))\]
\[f(x) = \frac{1}{x + 1} - \frac{1}{x + 3}\, ; \enspace D_{f} = \mathbb R \, \backslash \, \{-3;-1\}\]
\[f(-2) = \frac{1}{-2 + 1} - \frac{1}{-2 + 3} = -1 - 1 = -2\]
\[\Longrightarrow \quad \text{Hochpunkt}, HoP \, (-2|-2)\]
