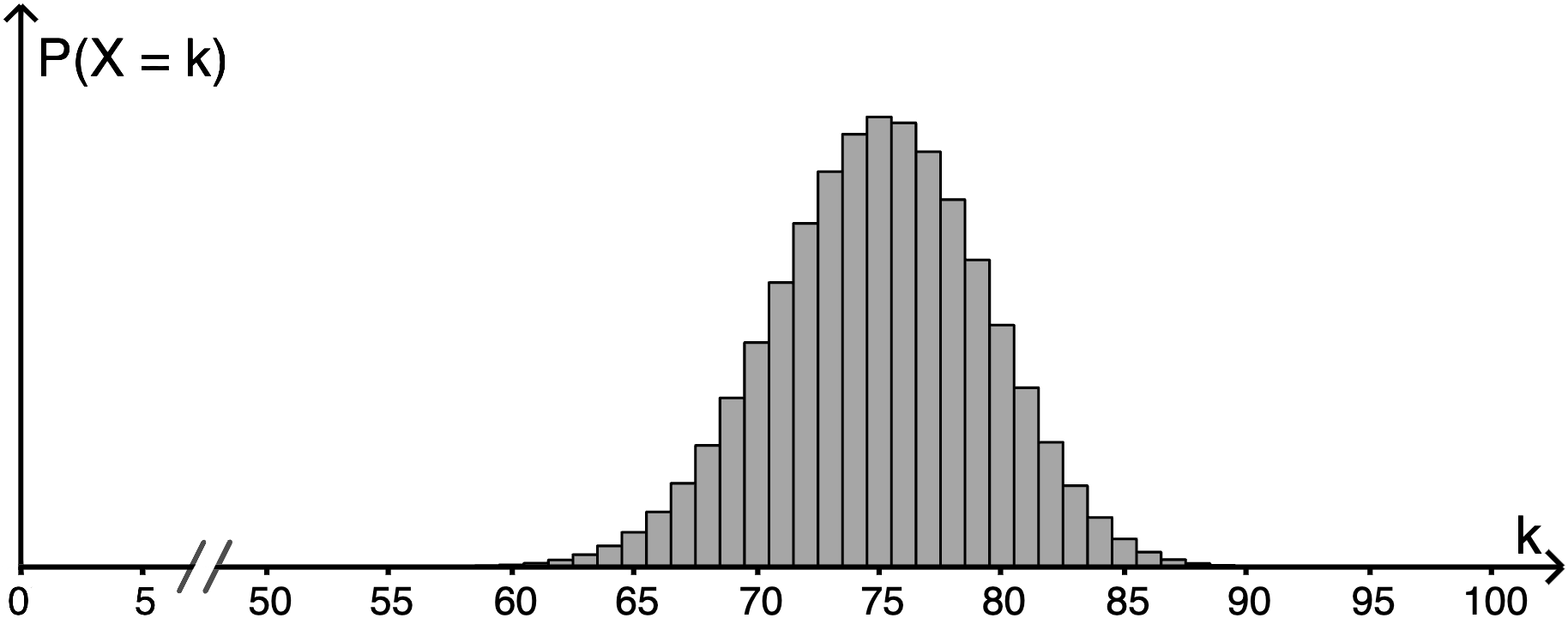
Der Erwartungswert von \(X\) ist ganzzahlig. Die Abbildung zeigt Werte der Wahrscheinlichkeitsverteilung von \(X\).
Bestimmen Sie die Anzahl der blauen Sektoren des Glücksrads.
(3 BE)
Lösung zu Teilaufgabe b
Der Abbildung ist zu entnehmen: \(\mu = 75\)
\[100 \cdot p = 75\; \Leftrightarrow \; p = \frac{75}{100} = 0{,}75\]
\[0{,}75 \cdot 20 = 15\]
15 Sektoren des Glücksrads sind blau eingefärbt.
Ausführliche Erklärung (nicht verlangt)
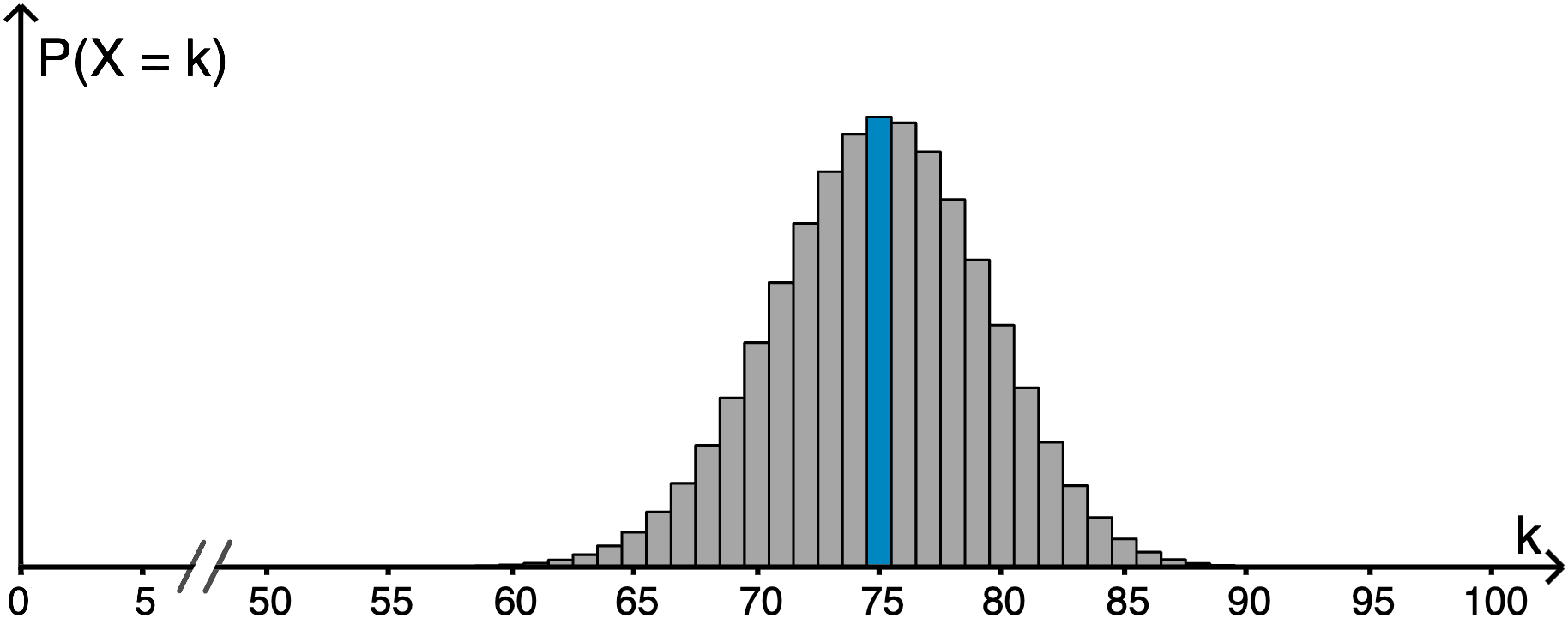
Bei einer Binomialverteilung treten die größten Wahrscheinlichkeiten in der Umgebung des Erwartungswerts oder am Erwartungswert auf. Der Wahrscheinlichkeitsverteilung von \(X\) ist zu entnehmen, dass \(\textcolor{#0087c1}{P(X = 75)}\) die maximale Wahrscheinlichkeit der Verteilung ist. Zudem ist der Erwartungswert von \(X\) ganzzahlig (vgl. Angabe). Folglich ist \(\mu = 75\) der Erwartungswert von \(X\).
Die Zufallsgröße \(X\) ist nach \(B(100;p)\) binomialverteilt. In Kenntnis des Erwartungswerts von \(X\) lässt sich die Trefferwahrscheinlichkeit \(p\) dafür berechnen, dass die Farbe „Blau" erzielt wird.
Erwartungswert \(\boldsymbol{\mu}\) einer binomialverteilten Zufallsgröße \(\boldsymbol{X}\)
\(\mu = E(X) = n \cdot p\) (vgl. Merkhilfe)
Varianz \(\boldsymbol{Var(X)}\) einer binomialverteilten Zufallsgröße \(\boldsymbol{X}\):
\(Var(X) = n \cdot p \cdot (1 - p)\) (vgl. Merkhilfe)
Standardabweichung \(\boldsymbol{\sigma}\) einer binomialverteilten Zufallsgröße \(\boldsymbol{X}\)
\[\sigma = \sqrt{Var(X)} = \sqrt{n \cdot p \cdot (1 - p)}\]
Wobei \(n\) die Länge der Bernoullikette und \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses ist.
\[\begin{align*}n \cdot p &= \mu \\[0.8em] 100 \cdot p &= 75 &&| : 100 \\[0.8em] p &= \frac{75}{100} = 0{,}75\end{align*}\]
Von den 20 gleich großen Sektoren des Glücksrads (vgl. Angabe) sind somit \(0{,}75 \cdot 20 = 15\) Sektoren blau eingefärbt.
