Abbildung 1 zeigt die Pyramide \(ABCDS\) mit den Eckpunkten \(A(-3|-3|0)\), \(B(3|-3|0)\), \(C(3|3|0)\), \(D(-3|3|0)\) und \(S(0|0|4)\) sowie den Punkt \(O(0|0|0)\), der in der quadratischen Grundfläche der Pyramide liegt. Die Seitenfläche \(CDS\) der Pyramide liegt in der Ebene \(E\).
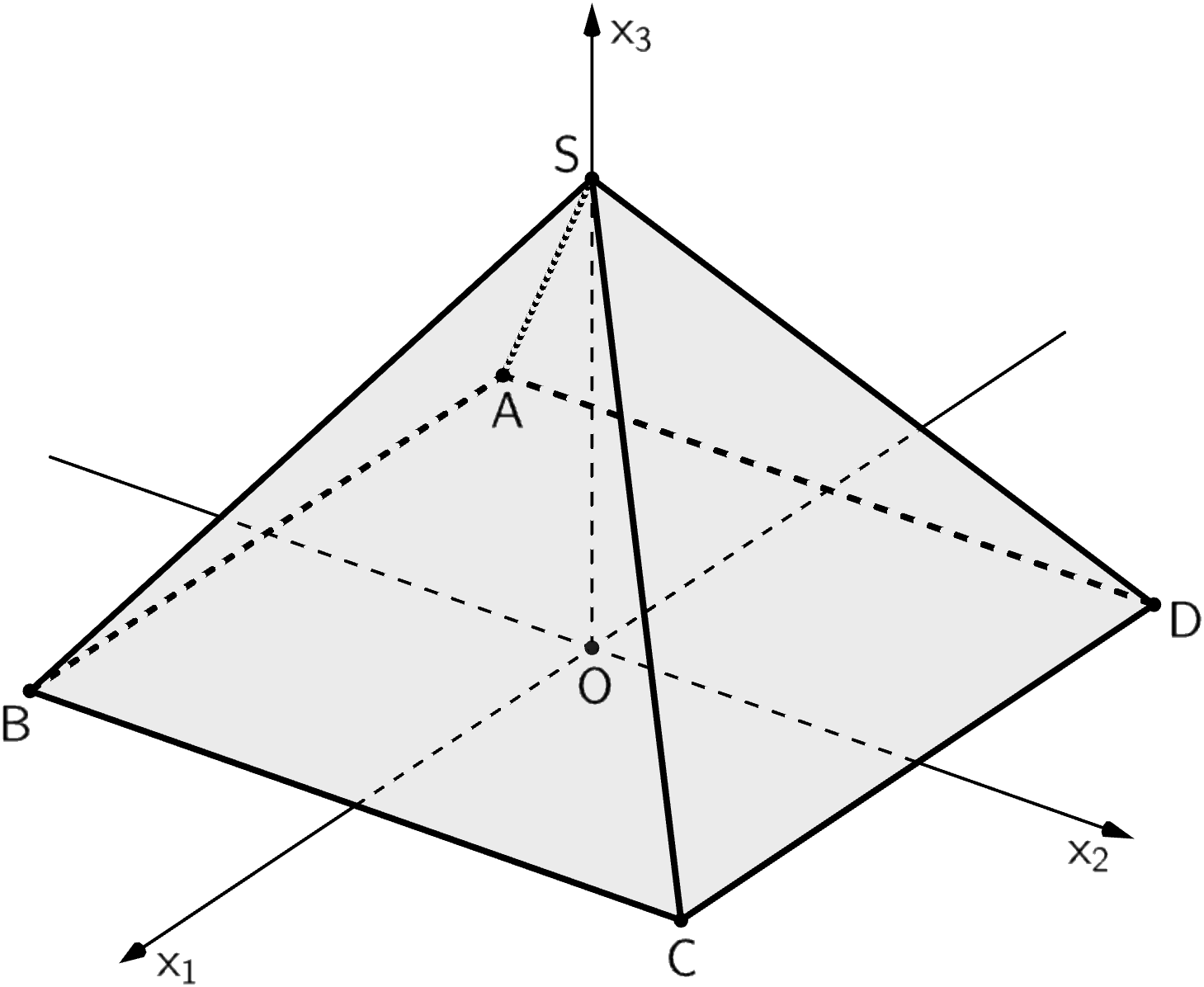Abb. 1
Berechnen Sie den Inhalt der Oberfläche der Pyramide.
(4 BE)
Lösung zu Teilaufgabe a
1. Möglichkeit: elementargeometrischer Ansatz
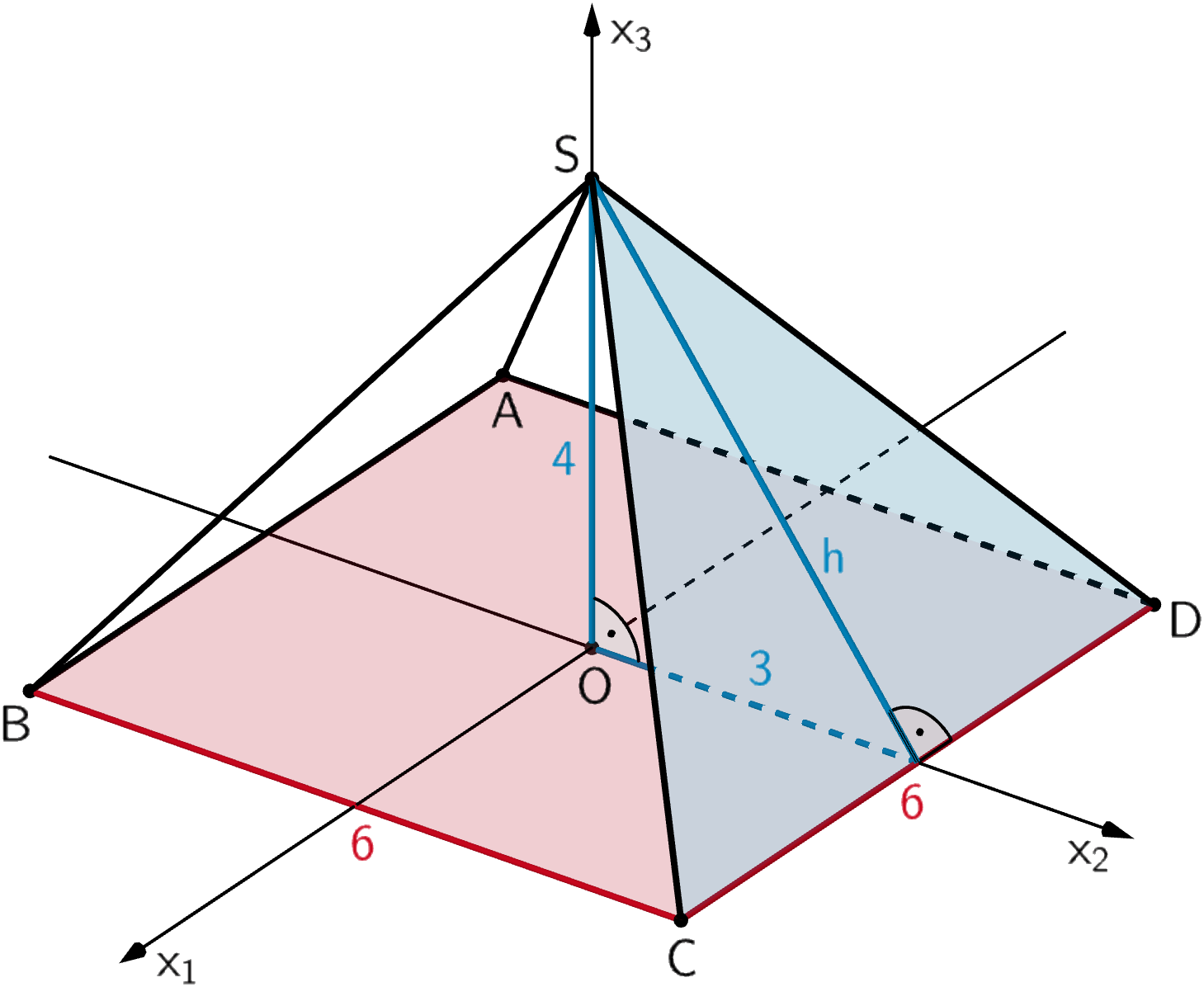
Die Oberfläche der geraden Pyramide (alle Seitenkanten sind gleich lang) setzt sich aus der quadratischen Grundfläche \(\textcolor{#cc071e}{ABCD}\) und vier kongruenten gleichschenkligen Dreiecken zusammen. Die Höhe \(\textcolor{#0087c1}{h}\) eines Dreiecks kann mithilfe des Satzes des Pythagoras bestimmt werden. Alle anderen benötigten Längenmaße ergeben sich anhand der Koordinaten der angegebenen Punkte.
\[\begin{align*}O_{ABCDS} &= \textcolor{#cc071e}{A_{ABCD}} + 4 \cdot \textcolor{#0087c1}{A_{CDS}} \\[0.8em] &= \textcolor{#cc071e}{6}^2 + 4 \cdot \frac{1}{2} \cdot \textcolor{#cc071e}{6} \cdot \textcolor{#0087c1}{h} &&| \; \textcolor{#0087c1}{h = \sqrt{3^2 + 4^2} = 5} \\[0.8em] &= \textcolor{#cc071e}{6}^2 + 4 \cdot \frac{1}{2} \cdot \textcolor{#cc071e}{6} \cdot \textcolor{#0087c1}{5} \\[0.8em] &= 36 + 4 \cdot 15 \\[0.8em] &= 96 \end{align*}\]
2. Möglichkeit: mithilfe des Vektorprodukts
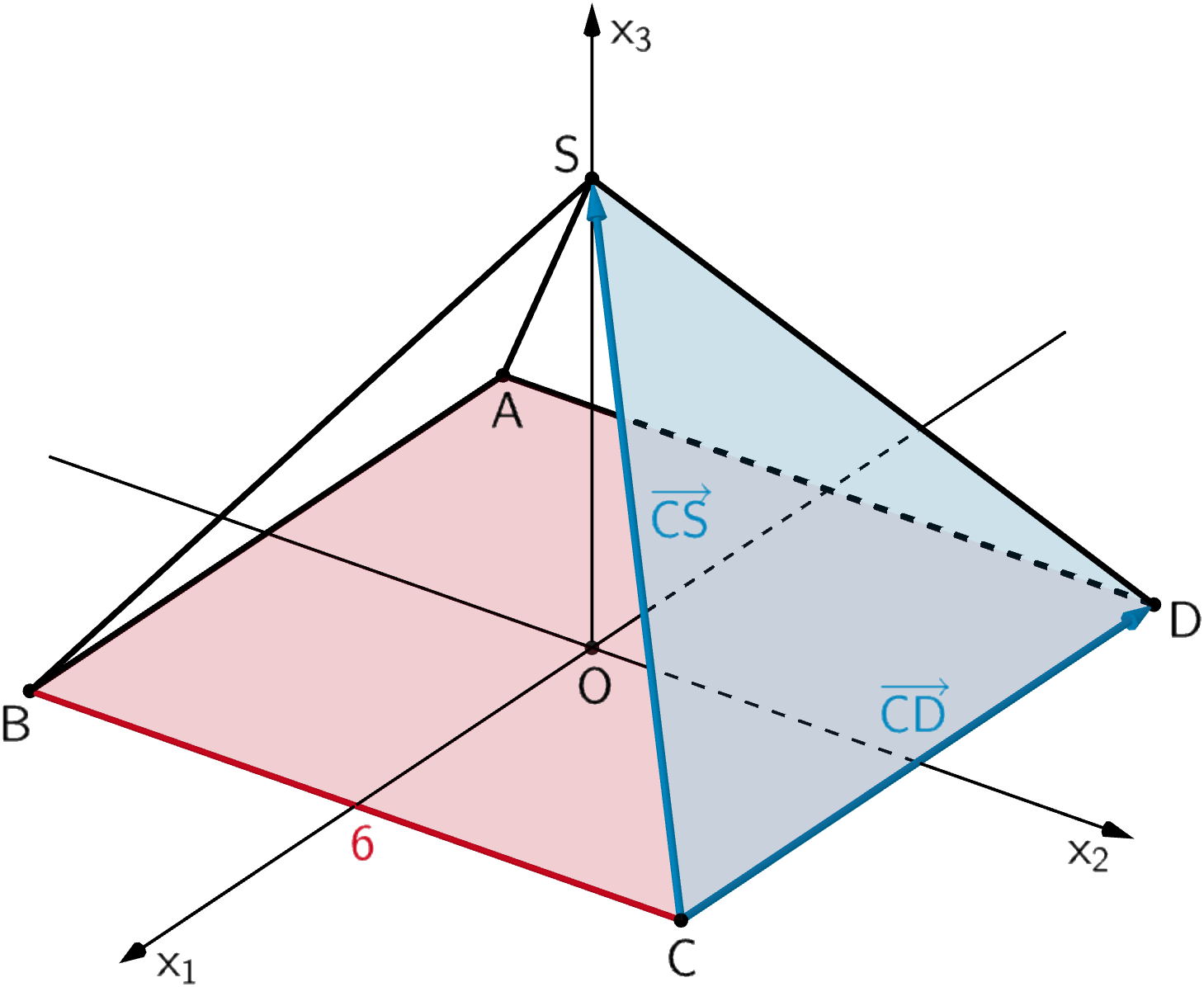
Der Inhalt einer der dreieckigen Seitenflächen lässt sich auch mithilfe des Vektorprodukts bestimmen, beispielsweise wie folgt:
\(C(3|3|0)\), \(D(-3|3|0)\), \(S(0|0|4)\)
Anwendung des Vekorprodukts
Der Betrag des Vektorprodukts \(\overrightarrow{a} \times \overrightarrow{b}\) entspricht der Maßzahl des Flächeninhalts eines von zwei Vektoren \(\overrightarrow{a} \neq \overrightarrow{0}\) und \(\overrightarrow{b} \neq \overrightarrow{0}\) aufgespannten Parallelogramms.
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \textcolor{#cc071e}{\vert \overrightarrow{b} \vert \cdot \sin{\varphi}}\]
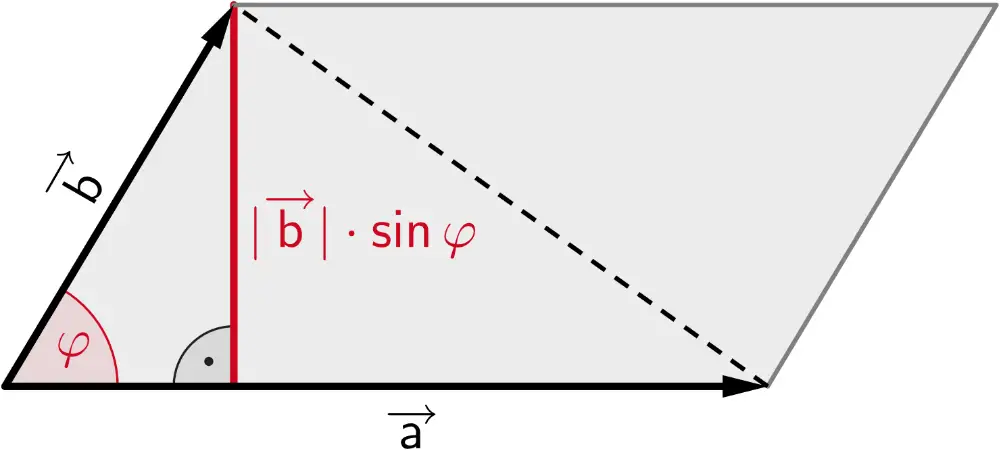
Flächeninhalt eines Parallelogramms
\[A = \vert \overrightarrow{a} \times \overrightarrow{b} \vert\]
Flächeninhalt eines Dreiecks
\[A = \frac{1}{2} \cdot \vert \overrightarrow{a} \times \overrightarrow{b} \vert\]
\[\textcolor{#0087c1}{\overrightarrow{CD}} = \overrightarrow{D} - \overrightarrow{C} = \begin{pmatrix} -3\\3\\0 \end{pmatrix} - \begin{pmatrix} 3\\3\\0 \end{pmatrix} = \textcolor{#0087c1}{\begin{pmatrix} -6\\0\\0 \end{pmatrix}}\]
\[\textcolor{#0087c1}{\overrightarrow{CS}} = \overrightarrow{S} - \overrightarrow{C} = \begin{pmatrix} 0\\0\\4 \end{pmatrix} - \begin{pmatrix} 3\\3\\0 \end{pmatrix} = \textcolor{#0087c1}{\begin{pmatrix} -3\\-3\\4 \end{pmatrix}}\]
Vektorprodukt (Kreuzprodukt)
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) mit den Eigenschaften:
\(\overrightarrow{c}\) ist sowohl zu \(\overrightarrow{a}\) als auch zu \(\overrightarrow{b}\) senkrecht.
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist gleich dem Produkt aus den Beträgen der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) und dem Sinus des von ihnen eingeschlossenen Winkels \(\varphi\).
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, dann weist \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) in Richtung des Mittelfingers.
Berechnung eines Vektorprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\]
\[\begin{align*}\textcolor{#0087c1}{A_{CDS}} &= \frac{1}{2} \cdot \vert \textcolor{#0087c1}{\overrightarrow{CD}} \times \textcolor{#0087c1}{\overrightarrow{CS}} \vert = \frac{1}{2} \cdot \left| \textcolor{#0087c1}{\begin{pmatrix} -6\\0\\0\end{pmatrix}} \times \textcolor{#0087c1}{\begin{pmatrix} -3\\-3\\4\end{pmatrix}} \right| \\[0.8em] &= \frac{1}{2} \cdot \left| \begin{pmatrix} 0 & \cdot & 4 & - & 0 & \cdot & (-3) \\ 0 & \cdot & (-3) & - & (-6) & \cdot & 4 \\ (-6) & \cdot & (-3) & - & 0 & \cdot & (-3) \end{pmatrix}\right|\\[0.8em] &= \frac{1}{2} \cdot \left| \begin{pmatrix} 0 \\ 24 \\ 18 \end{pmatrix} \right| = \frac{1}{2} \cdot \sqrt{0^2 + 24^2 + 18^2} = \frac{1}{2} \cdot 30 \\[0.8em] &= \textcolor{#0087c1}{15} \end{align*}\]
\[\begin{align*}O_{ABCDS} &= \textcolor{#cc071e}{A_{ABCD}} + 4 \cdot \textcolor{#0087c1}{A_{CDS}} \\[0.8em] &= \textcolor{#cc071e}{6}^2 + 4 \cdot \textcolor{#0087c1}{15} \\[0.8em] &= 96 \end{align*}\]
Anmerkung
Dieser Lösungsweg ist zwar rechenintensiver, dafür kann das Ergebnis des Vektorprodukts \(\overrightarrow{CD} \times \overrightarrow{CS}\) in Teilaufgabe c verwendet werden.
