Betrachtet wird der abgebildete Würfel \(ABCDEFGH\).
Die Eckpunkte \(D\), \(E\), \(F\) und \(H\) dieses Würfels besitzen in einem kartesischen Koordinatensystem die folgenden Koordinaten: \(D(0|0|-2)\), \(E(2|0|0)\), F(2|2|0) und \(H(0|0|0)\).
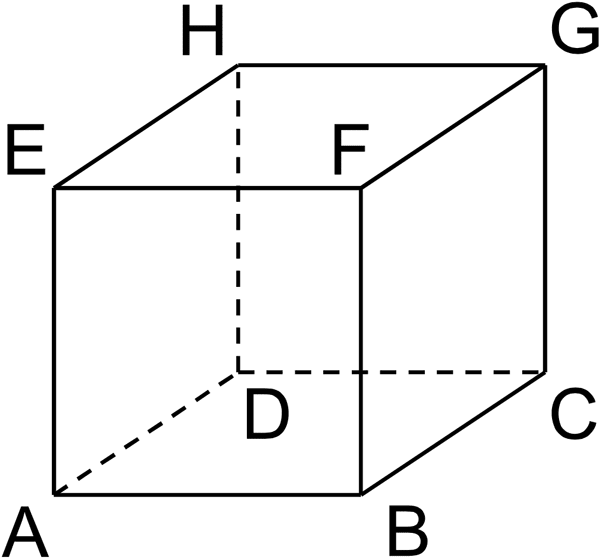
Zeichnen Sie in die Abbildung die Koordinatenachsen ein und bezeichnen Sie diese. Geben Sie die Koordinaten des Punkts \(A\) an.
(2 BE)
Lösung zu Teilaufgabe 1a
Lage eines geometrischen Körpers im Raum
Einzeichnen der Koordinatenachsen
\(D(0|0|-2)\), \(E(2|0|0)\), \(F(2|2|0)\), \(H(0|0|0)\)
Der Punkt \(H(0|0|0)\) liegt im Kootdinatenursprung. Der Punkt \(E(2|0|0)\) liegt auf der \(x_{1}\)-Achse. Folglich liegt der Punkt \(G\) auf der \(x_{2}\)-Achse. Der Punkt \(D(0|0|-3)\) liegt auf der negativen \(x_{3}\)-Achse.
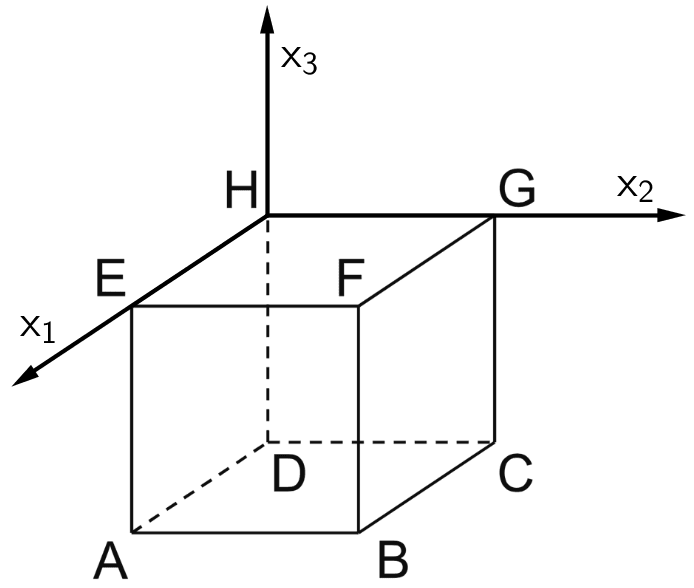
Lage des Koordinatensystems entsprechend der Koordinaten der Eckpunkte \(D\), \(E\), \(F\) und \(H\) des Würfels \(ABCDEFGH\).
Koordinaten des Punktes \(A\)
\(D(0|0|-2)\), \(E(2|0|0)\)
Der Abbildung zufolge gilt:
\[x_{{1}_{A}} = x_{{1}_{E}}; \enspace x_{{2}_{A}} = x_{{2}_{E}}; \enspace x_{{3}_{A}} = x_{{3}_{D}}\]
\[\Longrightarrow \quad A(2|0|-2)\]

