Zeigen Sie, dass Bedingung III weder bei der Modellierung mit \(p\) aus Aufgabe 1 noch bei einer Modellierung mit \(k\) erfüllt ist.
(2 BE)
Lösung zu Teilaufgabe 2b
Funktionswerte im Sachzusammenhang bewerten
\[p(x) = -0{,}2x^{2} + 5; \; D_{p} = [-5;5]\]
\[k(x) = 5 \cdot \cos\left( \frac{\pi}{10} \cdot x \right); \; D_{k} = [-5;5]\]
Bedingung III:
Der Tunnel ist auf einer Breite von mindestens 6 m mindestens 4 m hoch.
![Graph der Funktion p für x ∈ [-5;5], Punkte (-3|p(-3)) und (3|p(3)) Graph der Funktion p für x ∈ [-5;5], Punkte (-3|p(-3)) und (3|p(3))](/images/stories/B2016_PT_B_A_2/B2016_PT_B_A_2_2b_1.png)
![Graph der Funktion k für x ∈ [-5;5], Punkte (-3|k(-3)) und (3|k(3)) Graph der Funktion k für x ∈ [-5;5], Punkte (-3|k(-3)) und (3|k(3))](/images/stories/B2016_PT_B_A_2/B2016_PT_B_A_2_2b_2.png)
Das Intervall \(x \in [-3;3]\) entspricht bei der Modellierung einer zum Mittelpunkt \(M\) des Tunnelbodens symmetrischen Breite von 6 m. Um zu bestätigen, dass Bedingung III weder bei einer Modellierung mit \(p\) noch bei einer Modellierung mit \(k\) erfüllt ist, überprüft man die Funktionswerte \(p(-3)\) und \(p(3)\) bzw. \(k(-3)\) und \(k(3)\).
Damit Bedingung III erfüllt ist, muss gelten:
\(p(x) \geq 4\) für \(x \in [-3;3]\)
bzw.
\(k(x) \geq 4\) für \(x \in [-3;3]\)
Aufgrund der Achsensymmetrie zur \(y\)-Achse der Graphen der Funktionen \(p\) und \(k\) gilt \(p(-3) = p(3)\) bzw. \(k(-3) = k(3)\).
Nachweis der Achsensymmetrie zur \(y\)-Achse von \(G_{p}\) und \(G_{k}\):
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
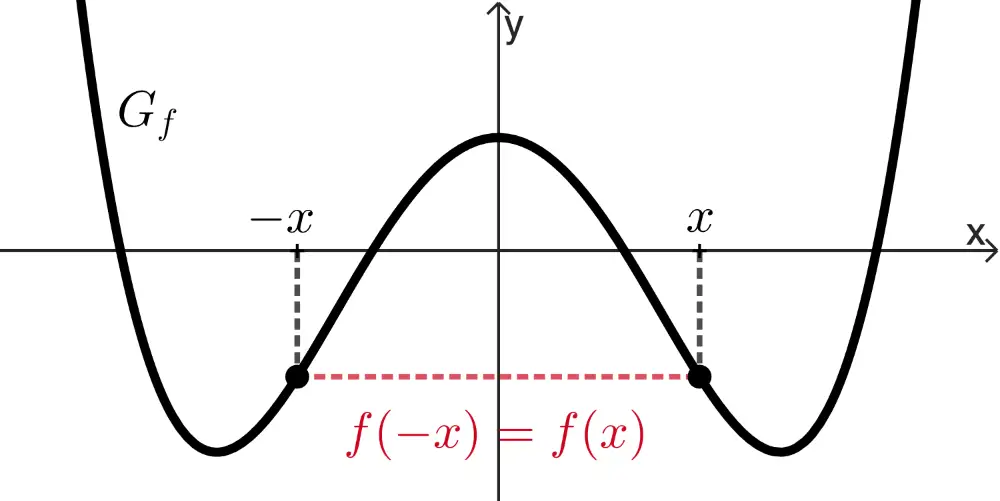
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
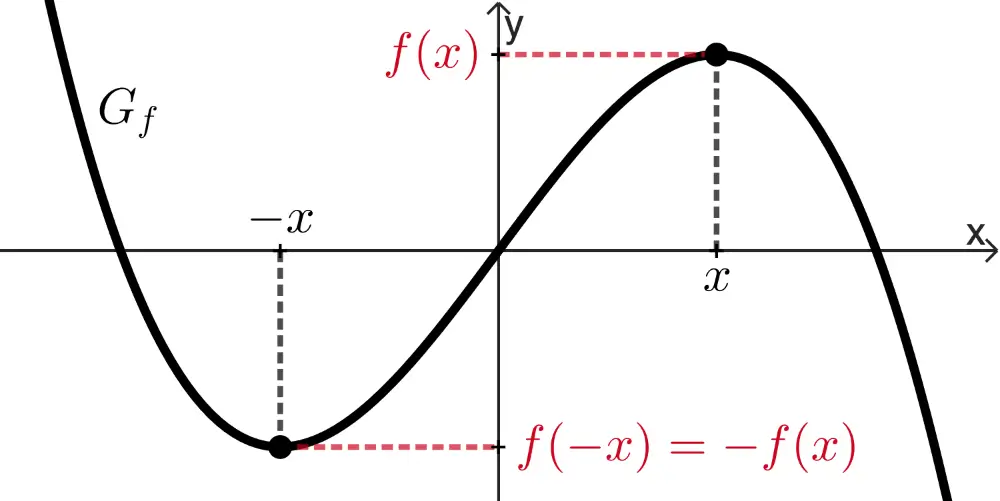
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
\[p(x) = -0{,}2x^{2} + 5; \; D_{p} = [-5;5]\]
\[k(x) = 5 \cdot \cos\left( \frac{\pi}{10} \cdot x \right); \; D_{k} = [-5;5]\]
\[p(-x) = -0{,}2 \cdot (-x)^{2} + 5 = -0{,}2x^{2} + 5 = p(x)\]
\[k(-x) = 5 \cdot \cos\left( \frac{\pi}{10} \cdot (-x) \right) = 5 \cdot \cos\left( \frac{\pi}{10} \cdot x \right) = k(x)\]
Funktionswerte \(p(-3)\) und \(p(3)\) bzw. \(k(-3)\) und \(k(3)\) berechnen:
\[p(-3) = p(3) = -0{,}2 \cdot 3^{2} + 5 = 3{,}2\]
\(\Longrightarrow \quad p(x) \geq 3{,}2\) für \(x \in [-3;3]\)
\[k(-3) = k(3) = 5 \cdot \cos\left( \frac{\pi}{10} \cdot 3 \right) \approx 2{,}94\]
\(\Longrightarrow \quad k(x) \geq 2{,}94\) für \(x \in [-3;3]\)
\(\Longrightarrow \quad\)Bedingung III ist weder bei einer Modellierung mit \(p\) noch bei einer Modellierung mit \(k\) erfüllt.


