Ein den oberen Rand des Kunstwerks genauer darstellendes Modell liefert der Graph der in \(\mathbb R\) definierten ganzrationalen Funktion \(q\) vierten Grades mit \(q(x) = -0{,}11x^4 - 0{,}81x^2 + 5\,\). Der Graph von \(q\) wird mit \(G_q\) bezeichnet.
Weisen Sie rechnerisch nach, dass \(G_q\) symmetrisch bezüglich der \(y\)-Achse ist, durch die Punkte \(A\) und \(B\) verläuft und genau einen Extrempunkt besitzt.
(7 BE)
Lösung zu Teilaufgabe 1b
\[q(x) = -0{,}11x^4 -0{,}81x^2 + 5 \,; \quad D_q = \mathbb R\]
Nachweis der Achsensymmetrie von \(G_q\)
Symmetrie von Funktionsgraphen bzgl. des Koordinatensystems
Der Graph einer Funktion \(f\) ist
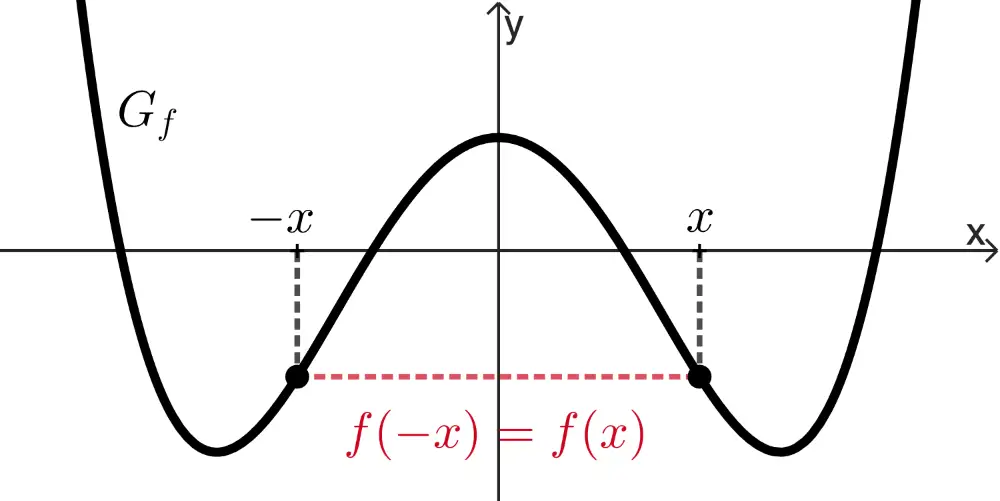
achsensymmetrisch bzgl. der \(\boldsymbol{y}\)-Achse,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = f(x)\).
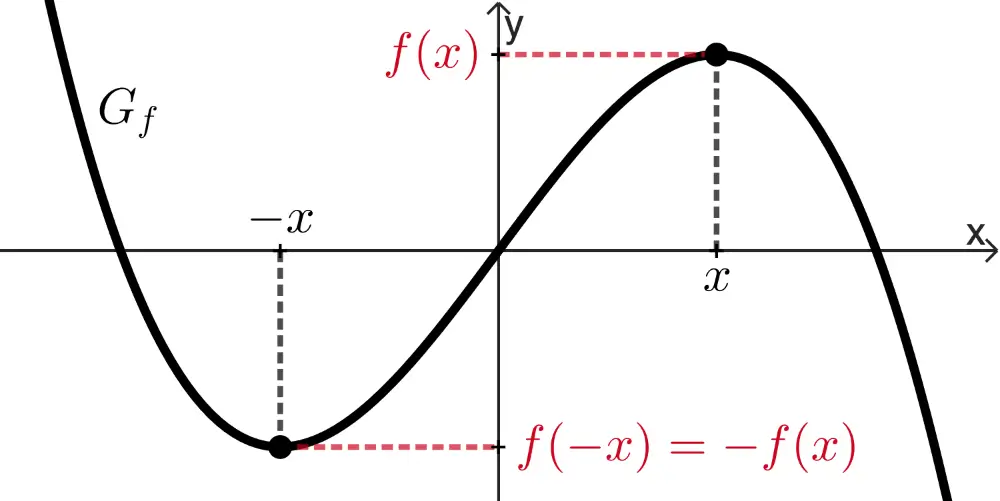
punktsymmetrisch bzgl. des Koordinatenursprungs,
wenn für alle \(x \in D_f\) gilt: \(f(-x) = -f(x)\)
\[\begin{align*} q(-x) &= -0{,}11(-x)^4 -0{,}81(-x)^2 + 5 \\[0.8em] &= -0{,}11x^4 - 0{,}81x^2 + 5 \\[0.8em] &= q(x) \end{align*}\]
Nachweis: \(A\,,\,B\, \in q\)
1. Lösungsansatz: Punktprobe
\[A\,(-2|0)\,, \quad B\,(2|0)\,, \quad q(x) = -0{,}11x^4 -0{,}81x^2 + 5\]
\[\begin{align*} A \in q \, \colon \enspace 0 &= -0{,}11 \cdot (-2)^4 - 0{,}81 \cdot (-2)^2 + 5 \\[0.8em] 0 &= -0{,}11 \cdot 16 - 0{,}81 \cdot 4 + 5 \\[0.8em] 0 &= -1{,}76 - 3{,}24 + 5 \\[0.8em] 0 &= 0 \enspace (\text{w}) \end{align*}\]
\[\begin{align*} B \in q \, \colon \enspace 0 &= -0{,}11 \cdot 2^4 - 0{,}81 \cdot 2^2 + 5 \\[0.8em] 0 &= -0{,}11 \cdot 16 - 0{,}81 \cdot 4 + 5 \\[0.8em] 0 &= -1{,}76 - 3{,}24 + 5 \\[0.8em] 0 &= 0 \enspace (\text{w}) \end{align*}\]
2. Lösungsansatz: Nullstellen von \(q\)
\[A\,(-2|0)\,, \quad B\,(2|0)\,, \quad q(x) = -0{,}11x^4 -0{,}81x^2 + 5\]
Die Punkte \(A\) und \(B\) liegen auf der \(x\)-Achse.
Nullstellen von \(q\) berechnen:
\[\begin{align*} -0{,}11x^4 - 0{,}81x^2 + 5 &= 0 & &| \; \text{Substitution:} \enspace u = x^2 \\[0.8em] -0{,}11u^2 -0{,}81u + 5 &= 0 \end{align*}\]
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[\begin{align*} u_{1,2} &= \frac{0{,}81 \pm \sqrt{(-0{,}81)^2 - 4 \cdot (-0{,}11) \cdot 5}}{2 \cdot (-0{,}11)} \\[0.8em] &= \frac{0{,}81 \pm 1{,}69}{-0{,}22} \\[0.8em] u_1 &= -\frac{125}{11} \quad \vee \quad u_2 = 4 \end{align*}\]
Resubstitution:
\[\begin{align*} x^2 &= u_1 \\[0.8em] x^2 &= -\frac{125}{11} & &\Longrightarrow \quad \text{keine Lösung} \\[2.4em] x^2 &= u_2 \\[0.8em] x^2 &= 4 & &| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm 2 \end{align*}\]
\[\Longrightarrow \quad A\,(-2|0)\, \enspace B\,(2|0)\]
Nachweis des einzigen Extrempunktes von \(G_q\)
\[g(x) = -0{,}11x^4 -0{,}81x^2 + 5 \,, \quad D_q = \mathbb R\]
Notwendige Bedingung: \(\;q'(x) \overset{!}{=} 0\)
Erste Ableitung \(q'(x)\) bilden:
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[\begin{align*}q'(x) &= -0{,}11 \cdot 4x^3 - 0{,}81 \cdot 2x \\[0.8em] &= -0{,}44x^3 - 1{,}62x \\[0.8em] &= -x\big( 0{,}44x^2 + 1{,}62 \big) \end{align*}\]
\[-x\big( \underbrace{0{,}44x^2 + 1{,}62}_{>\,0}\big) = 0\]
\(\Longrightarrow \quad x = 0\) ist einzige Nullstelle von \(g'(x)\,\). Folglich kann \(G_q\) nur einen Extrempunkt besitzen.
Extrempunkt bestätigen bzw. Terrassenpunkt ausschließen:
Anwendung der Differetialrechnung:
Terrassenpunkt
Wenn \(f'(x_0) = f''(x_0) = 0\) ist und \(f''\) an der Stelle \(x_0\) das Vorzeichen wechselt, so hat \(G_f\) an der Stelle \(x_0\) einen Terrassenpunkt.
Zweite Ableitung g''(x) bilden:
Ableitung einer Potenzfunktion
\[f(x) = x^r \quad \Longrightarrow \quad f'(x) = rx^{r - 1} \quad (r \in \mathbb R)\]
(vgl. Merkhilfe)
\[\begin{align*} g'(x) = -0{,}44x^3 - 1{,}62x \quad \Longrightarrow \quad g''(x) &= -0{,}44 \cdot 3x^2 - 1{,}62 \\[0.8em] &= -1{,}32x^2 -1{,}62\end{align*}\]
\[q''(0) = -1{,}62\]
\(q''(0) \neq 0 \quad \Longrightarrow \quad G_q\,\) besitzt genau einen Extrempunkt.
Ergänzung: Art und Lage des Extrempunkts
Anwendung der Differentialrechnung:
Art von Extrempunkten mithilfe der zweiten Ableitung nachweisen
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) > 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Minimum (Tiefpunkt).
Ist \(f'(x_{0}) = 0\) und \(f''(x_{0}) < 0\), so hat der Graph \(G_{f}\) an der Stelle \(x_{0}\) ein relatives Maximum (Hochpunkt).
\(\left. \begin{align*} q'(0) &= 0 \\[0.8em] q''(0) &< 0 \end{align*} \right\} \Longrightarrow \quad\) \(G_q\) hat an der Stelle \(x = 0\) ein lokales Maximum.
\[g(0) = -0{,}11 \cdot 0^4 -0{,}81 \cdot 0^2 + 5 = 5\]
\(\Longrightarrow \quad\) Der Punkt \(C\,(0|5)\) (siehe Teilaufgabe 1a) ist Hochpunkt und einziger Extrempunkt von \(G_q\,\).


