Die Größen der Sektoren werden geändert. Dabei werden der grüne und der rote Sektor verkleinert, wobei der Mittelpunktswinkel des roten Sektors wieder doppelt so groß wie der des grünen Sektors ist. Die Abbildung zeigt einen Teil eines Baumdiagramms, das für das geänderte Glücksrad die beiden ersten Drehungen beschreibt. Ergänzend ist für einen Pfad die zugehörige Wahrscheinlichkeit angegeben.
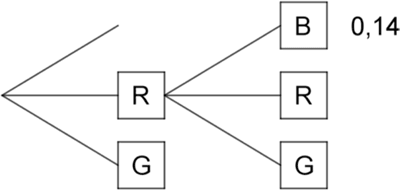
Bestimmen Sie die Größe des zum grünen Sektor gehörenden Mittelpunktswinkels.
(5 BE)
Lösung zu Teilaufgabe 2c
Es sei \(p\) die Wahrscheinlichkeit, mit der der grüne Sektor erscheint.
\[P(G) = p\]
„... wobei der Mittelpunktswinkel des roten Sektors wieder doppelt so groß wie der des grünen Sektors ist."
\[P(R) = 2p\]
\[P(B) = 1 - P(G) - P(R) = 1 - p - 2p = 1 - 3p\]
Entsprechend des abgebildeten Teils eines Baumdiagramms gilt nach der ersten Pfadregel:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*}P(R) \cdot P(B) &= P(R \cap B) \\[0.8em] 2p \cdot (1 - 3p) &= 0{,}14 \\[0.8em] 2p - 6p^{2} &= 0{,}14 &&| -0{,}14 \\[0.8em] -6p^{2} +2p -0{,}14 &= 0 \end{align*}\]
Mithilfe der Lösungsformel für quadratische Gleichungen folgt:
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[\begin{align*}p_{1,2} &= \frac{-2 \pm \sqrt{2^{2} - 4 \cdot (-6) \cdot (-0{,}14)}}{2 \cdot (-6)} \\[0.8em] &= \frac{-2 \pm 0{,}8}{-12} \end{align*}\]
\[p_{1} = 0{,}1 \; \vee \; \left( p_{2} = \frac{7}{30} > \frac{1}{6} \right)\]
Da der grüne Sektor verkleinert wird, gilt \(p < \dfrac{1}{6}\) (ursprünglicher Wert). Somit ist \(p = 0{,}1\) die im Sachzusammenhang richtige Lösung.
Mittelpunktswinkel des grünen Sektors berechnen:
\(0{,}1 \cdot 360^{\circ} = 36^{\circ}\)
Der grüne Sektor hat einen Mittelpunktswinkels von 36°.


