Gegeben sind die Punkte \(A(0|0|0)\), \(B(3|4|1)\), \(C(1|7|3)\), \(D(-2|3|2)\).

  1. Weisen Sie nach, dass das Viereck \(ABCD\) ein Parallelogramm ist.
    (1 BE)
  2. Der Punkt \(T\) liegt auf der Strecke \(\overline{AC}\). Das Dreieck \(ABT\) hat bei \(B\) einen rechten Winkel. Ermitteln Sie das Verhältnis der Länge der Strecke \(\overline{AT}\) zur Länge der Strecke \(\overline{CT}\).
    (4 BE)

Lösung zu Aufgabe A9

 

\(A(0|0|0)\), \(B(3|4|1)\), \(C(1|7|3)\), \(D(-2|3|2)\)

 

a) Nachweis, dass das Viereck \(ABCD\) ein Parallelogramm ist

Es ist beispielsweise nachzuweisen, dass die Seiten \(\textcolor{#cc071e}{\overline{AC}}\) und \(\textcolor{#cc071e}{\overline{CD}}\) zueinander parallel und gleich lang sind (schematische Darstellung).

\[\begin{align*} \textcolor{#cc071e}{\overrightarrow{AB}} &= \textcolor{#cc071e}{\overrightarrow{DC}} \\[0.8em] \overrightarrow{OB} -\overrightarrow{OA} &= \overrightarrow{OC} - \overrightarrow{OD} \\[0.8em] \begin{pmatrix} 3\\4\\1 \end{pmatrix} - \begin{pmatrix} 0\\0\\0 \end{pmatrix} &= \begin{pmatrix} 1\\7\\3 \end{pmatrix} - \begin{pmatrix} -2\\3\\2 \end{pmatrix} \\[0.8em] \textcolor{#cc071e}{\begin{pmatrix} 3\\4\\1 \end{pmatrix}} &= \textcolor{#cc071e}{\begin{pmatrix} 3\\4\\1 \end{pmatrix}} \\[0.8em] \Rightarrow \; \textcolor{#cc071e}{\vert \overline{AB}\vert} &= \textcolor{#cc071e}{\vert \overline{CD}\vert}\end{align*}\]

 

(Vgl. Mathematik Abiturskript Bayern G9 - 3 Geometrie, 3.2.6 Nachweis von Vierecken)

NEU  Abiturskript G9 PDF

 

b) Verhältnis der Länge der Strecke \(\overline{AT}\) zur Länge der Strecke \(\overline{CT}\)

Parallelogramm ABCD, Punkt T auf der Strecke AS, Dreieck ABT mit rechtem Winkel bei B

Planskizze (optional): Da das Dreieck \(ABT\) bei \(B\) rechtwinklig ist, legt die Bedingung \(\textcolor{#cc071e}{\overrightarrow{AB}} \perp \textcolor{#0087c1}{\overrightarrow{BT}}\) die Lage des Punktes \(T\) auf der Strecke \(\textcolor{#e9b509}{\overline{AC}}\) fest (schematische Darstellung).

Vorgehensweise

1. Strecke \(\textcolor{#e9b509}{\overline{AC}}\) in Parameterform formulieren.

2. Ortsvektor des Punktes \(T \in \textcolor{#e9b509}{\overline{AC}}\) mithilfe der Koordinaten der Strecke \(\textcolor{#e9b509}{\overline{AC}}\) ausdrücken.

3. Skalarprodukt zueinander senkrechter Vektoren anwenden.

\(\textcolor{#cc071e}{\overrightarrow{AB}} \perp \textcolor{#0087c1}{\overrightarrow{BT}} \; \Leftrightarrow \; \textcolor{#cc071e}{\overrightarrow{AB}} \circ \textcolor{#0087c1}{\overrightarrow{BT}} = 0\)

4. Verhältnis der Länge der Strecke \(\overline{AT}\) zur Länge der Strecke \(\overline{CT}\) ermitteln.

 

Strecke \(\boldsymbol{\textcolor{#e9b509}{\overline{AC}}}\) in Parameterform

Gleichung einer Gerade/Strecke in Parameterform

Gleichung einer Gerade/Strecke in Parameterform

Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform \(g \colon \overrightarrow{x} = \overrightarrow{OA} + \lambda \cdot \overrightarrow{u}\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden. Dabei ist \(\overrightarrow{OA}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).

Punkt-Richtung-Form

Ein Punkt \(\textcolor{#0087c1}{A} \in g\) und ein Richtungsvektor \(\textcolor{#cc071e}{\overrightarrow{u}}\,\) legen eine Gerade \(g\) fest.

Veranschaulichung der Punkt-Richtung-Form der Gleichung einer Gerade in Parameterform

\[\qquad \qquad \qquad g \colon \overrightarrow{x} = \textcolor{#0087c1}{\overrightarrow{OA}} + \lambda \cdot \textcolor{#cc071e}{\overrightarrow{u}}\]

Zwei-Punkt-Form

Zwei Punkte \(\textcolor{#0087c1}{A} \in g\) und \(\textcolor{#0087c1}{B} \in g\) legen eine Gerade \(g\) fest.

Veranschaulichung der Zwei-Punkte-Form der Gleichung einer Gerade in Parameterform

\[\qquad \qquad \qquad g \colon \overrightarrow{x} = \textcolor{#0087c1}{\overrightarrow{OA}} + \lambda \cdot \textcolor{#cc071e}{\overrightarrow{AB}}\]

Für \(\boldsymbol{\lambda \in [0;1]}\) beschreibt die Gleichung  \(\overrightarrow{x} = \textcolor{#0087c1}{\overrightarrow{OA}} + \lambda \cdot \textcolor{#cc071e}{\overrightarrow{AB}}\) die Strecke \(\boldsymbol{\overline{AB}}\).

\[\textcolor{#e9b509}{\overline{AC}}\colon \, \overrightarrow{x} = \overrightarrow{OA} + \lambda \cdot \overrightarrow{AC}, \; \lambda \in [0;1]\]

 

\(\overrightarrow{AC} = \overrightarrow{OC} = \begin{pmatrix} 1\\7\\3 \end{pmatrix}\) (da \(A(0|0|0)\))

 

\[\textcolor{#e9b509}{\overline{AC}} \colon \, \overrightarrow{x} = \begin{pmatrix} 0\\0\\0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 1\\7\\3 \end{pmatrix} =\lambda \cdot \begin{pmatrix} 1\\7\\3 \end{pmatrix}, \; \lambda \in [0;1]\]

 

Ortsvektor des Punktes \(\boldsymbol{T}\) 

Der Punkt \(T\) liegt auf der Strecke \(\textcolor{#e9b509}{\overline{AC}}\). Der Ortsvektor \(\overrightarrow{OT}\) lässt sich somit mithilfe der Gleichung der Strecke \(\textcolor{#e9b509}{\overline{AC}}\) in Abhängigkeit des Parameters \(\lambda\) ausdrücken.

 

\[T \in \textcolor{#e9b509}{\overline{AC}} \colon \, \overrightarrow{OT} =\lambda \cdot \begin{pmatrix} 1\\7\\3 \end{pmatrix} = \begin{pmatrix} \lambda\\7\lambda\\3\lambda \end{pmatrix}, \; \lambda \in [0;1]\]

 

Skalarprodukt der Vektoren \(\boldsymbol{\textcolor{#cc071e}{\overrightarrow{AB}} \perp \textcolor{#0087c1}{\overrightarrow{BT}}}\)

Skalarprodukt - zueinander senkrechte Vektoren

Anwendung des Skalarprodukts

Zueinander senkrechte (orthogonale) Vektoren

Zwei vom Nullvektor verschiedene Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) sind genau dann zueinander senkrecht (orthogonal), wenn deren Skalarprodukt null ist.

\[\textcolor{#cc071e}{\overrightarrow{a}} \circ \textcolor{#0087c1}{\overrightarrow{b}} = 0 \; \Leftrightarrow \; \textcolor{#cc071e}{\overrightarrow{a}} \perp \textcolor{#0087c1}{\overrightarrow{b}}\]

\[\begin{align*}\textcolor{#cc071e}{\overrightarrow{AB}} \circ \textcolor{#0087c1}{\overrightarrow{BT}} &= 0 &&|\; \overrightarrow{AB} = \overrightarrow{OB}, \;\text{da}\; A(0|0|0) \\[0.8em] \overrightarrow{OB} \circ (\overrightarrow{OT} - \overrightarrow{OB}) &= 0 \\[0.8em] \begin{pmatrix} 3\\4\\1 \end{pmatrix} \circ \left[\begin{pmatrix} \lambda\\7\lambda\\3\lambda \end{pmatrix} - \begin{pmatrix} 3\\4\\1 \end{pmatrix} \right] &= 0 \\[0.8em] \begin{pmatrix} 3\\4\\1 \end{pmatrix} \circ \begin{pmatrix} \lambda - 3\\7\lambda - 4\\3\lambda - 1 \end{pmatrix} &= 0 \\[0.8em] 3 \cdot (\lambda - 3) + 4 \cdot (7\lambda - 4) + 1 \cdot (3\lambda - 1) &= 0 \\[0.8em] 3\lambda - 9 + 28\lambda -16 + 3\lambda - 1 &= 0 \\[0.8em] 34\lambda - 26 &= 0 &&| + 26 \\[0.8em] 34\lambda &= 26 &&| : 34 \\[0.8em] \lambda &= \frac{26}{34} \\[0.8em] &= \frac{13}{17}\end{align*}\]

 

Verhältnis der Länge der Strecke \(\boldsymbol{\overline{AT}}\) zur Länge der Strecke \(\boldsymbol{\overline{CT}}\)

 

\[\textcolor{#e9b509}{\overline{AC}} \colon \, \overrightarrow{x} =\lambda \cdot \begin{pmatrix} 1\\7\\3 \end{pmatrix}, \; \lambda \in [0;1]\]

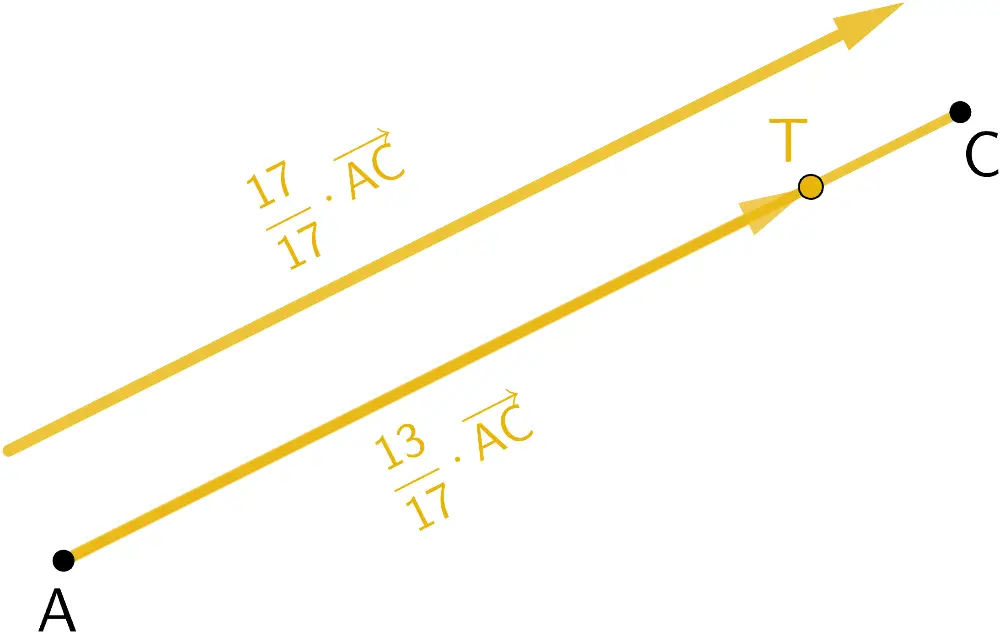
Veranschaulichung des Verhältnisses der Länge der Strecke AT zur Länge der Strecke CT

 

\(\lambda = \dfrac{13}{17}\) in die Gleichung der Strecke \(\textcolor{#e9b509}{\overline{AC}}\) eigesetzt, ergibt den Ortsvektor des Punktes \(T\).

\(\lambda = 1 = \dfrac{17}{17}\) in die Gleichung der Strecke \(\textcolor{#e9b509}{\overline{AC}}\) eigesetzt, ergibt den Ortsvektor des Punktes \(C(1|7|3)\).

Somit beträgt das Verhältnis der Länge der Strecke \(\overline{AT}\) zur Länge der Strecke \(\overline{CT}\)  \(13 : 4\).

 

(Vgl. Mathematik Abiturskript Bayern G9 - 3 Geometrie, 3.2.2 Skalarprodukt zweier Vektoren - Anwendungen des Skalarprodukts)

NEU  Abiturskript G9 PDF