Das Ende der Rechtskurve wird im Koordinatensystem durch den Punkt \(C\) beschrieben. Begründen Sie, dass für den Ortsvektor des Punkts \(C\) gilt: \(\overrightarrow{C} = \overrightarrow{M} + \overrightarrow{v}\).
(2 BE)
Lösung zu Teilaufgabe d
Vektorgleichung nachweisen
\[\overrightarrow{C} = \overrightarrow{M} + \overrightarrow{v}\]
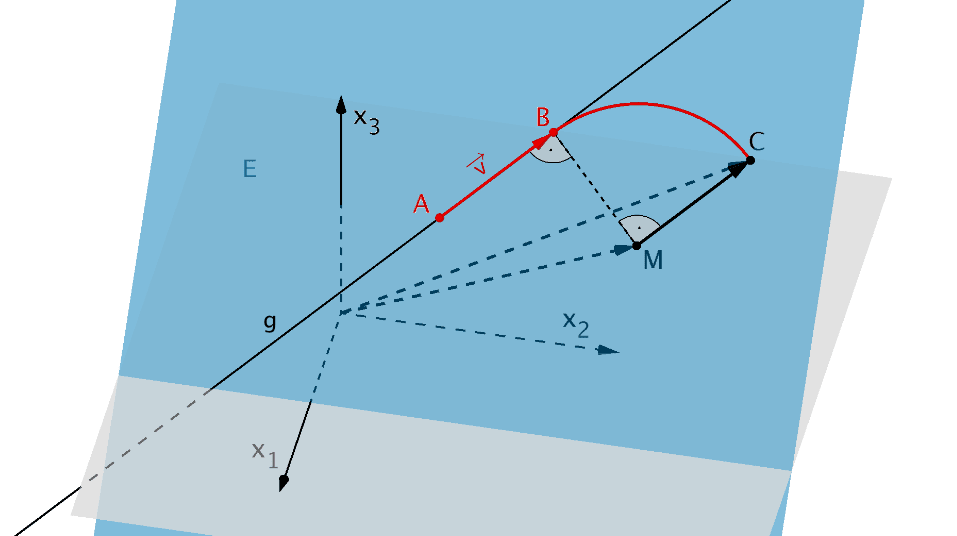
Richtungsvektor \(\overrightarrow{v}\) der Geraden \(g\), Ortsvektor \(\overrightarrow{C}\), Ostvektor \(\overrightarrow{M}\) und Vektor \(\overrightarrow{MC}\)
Die Rechtskurve, die im Modell durch einen Viertelkreis beschrieben wird, schließt an den geraden Abschnitt \([AB]\) an (siehe Angabe Teilaufgabe c). Das bedeutet, dass die Strecke \([MC]\) parallel zur Geraden \(g\) verläuft und folglich auch der Vektor \(\overrightarrow{MC}\) parallel zum Richtungsvektor \(\overrightarrow{v}\) der Geraden \(g\) ist. Da sich der Ortsvektor \(\overrightarrow{C}\) durch die Vektoraddition \(\overrightarrow{C} = \overrightarrow{M} + \overrightarrow{MC}\) beschreiben lässt, muss die Länge des Richtungsvektors \(\overrightarrow{v}\) der Geraden \(g\) gleich der Länge des Vektors \(\overrightarrow{MC}\) sein, damit \(\overrightarrow{C} = \overrightarrow{M} + \overrightarrow{v}\) gilt.
\[\overrightarrow{C} = \overrightarrow{M} + \overrightarrow{MC}\]
\[\overrightarrow{MC} \parallel \overrightarrow{v}\]
Der Radius des Viertelkreisbogens und damit auch die Länge der Strecke \([MC]\) ist aus Teilaufgabe c bekannt.
\[r = \overline{MB} = \overline{MC} = 2\]
Nachweis, dass \(\vert \overrightarrow{v} \vert = \overline{MC} = 2\) gilt:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\(\overrightarrow{v} = \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix}\) (siehe Teilaufgabe a,b)
\[\begin{align*} \vert \overrightarrow{v} \vert &= \left| \begin{pmatrix} -1 \\ \sqrt{2} \\ 1 \end{pmatrix} \right| \\[0.8em] &= \sqrt{(-1)^{2} + (\sqrt{2})^{2} + 1^{2}} \\[0.8em] &= \sqrt{4} \\[0.8em] &= 2 \end{align*}\]
\[\left. \begin{align*} &\overrightarrow{MC} \parallel \overrightarrow{v} \\[0.8em] &\vert \overrightarrow{v} \vert = \overline{MC} \end{align*} \right\} \enspace \Rightarrow \enspace \overrightarrow{v} = \overrightarrow{MC}\]
\[\left. \begin{align*} &\overrightarrow{C} = \overrightarrow{M} + \overrightarrow{MC} \\[0.8em] &\overrightarrow{v} = \overrightarrow{MC} \end{align*} \right\} \enspace \Rightarrow \enspace \overrightarrow{C} = \overrightarrow{M} + \overrightarrow{v}\]


