Bestimmen Sie den Flächeninhalt des Trapezes \(ABCD\).
(zur Kontrolle: 374)
(3 BE)
Lösung zu Teilaufgabe b
1. Möglichkeit: Formel für den Flächeninhalt eines Trapezes anwenden

Da das Trapez \(ABCD\) bei \(D\) einen rechten Innenwinkel hat (vgl. Teilaufgabe a), ist \(\vert \textcolor{#e9b509}{\overrightarrow{DA}}\vert\) die Höhe des Trapezes.
Flächeninhalt eines Trapezes

\[A = \frac{1}{2} \cdot (a + c) \cdot h\]
\(A(17|-10|0)\), \(B(17|20|0)\)
\[\textcolor{#cc071e}{\overrightarrow{AB}} = \overrightarrow{OB} - \overrightarrow{OA} = \begin{pmatrix} 17\\20\\0 \end{pmatrix} - \begin{pmatrix} 17\\-10\\0 \end{pmatrix} = \textcolor{#cc071e}{\begin{pmatrix} 0 \\ 30 \\ 0 \end{pmatrix}}\]
\(\textcolor{#0087c1}{\overrightarrow{DC}} = \textcolor{#0087c1}{\begin{pmatrix} 0 \\ 14 \\ 0 \end{pmatrix}}\), \(\textcolor{#e9b509}{\overrightarrow{DA}} = \textcolor{#e9b509}{\begin{pmatrix} 15 \\ 0 \\ -8 \end{pmatrix}}\) (vgl. Teilaufgabe a)
Der Betrag eines Vektors \(\overrightarrow{a}\) bedeutet die Länge eines zu \(\overrightarrow{a}\) gehörenden Repräsentanten. Schreibweise: \(\vert \overrightarrow{a}\vert\)
Für \(\smash{\overrightarrow{a} = \begin{pmatrix} a_1\\a_2 \end{pmatrix}}\vphantom{\begin{pmatrix} a_1\\a_2\\a_3 \end{pmatrix}}\) gilt \(\vert \overrightarrow{a}\vert = \sqrt{a_1^2 + a_2^2}\)
Für \(\overrightarrow{a} = \begin{pmatrix} a_1\\a_2\\a_3 \end{pmatrix}\) gilt \(\vert \overrightarrow{a}\vert = \sqrt{a_1^2 + a_2^2 + a_3^2}\)
\[\begin{align*}A_{ABCD} &= \frac{1}{2} \cdot \bigg(\vert \textcolor{#cc071e}{\overrightarrow{AB}}\vert + \vert \textcolor{#0087c1}{\overrightarrow{DC}} \vert\bigg) \cdot \vert \textcolor{#e9b509}{\overrightarrow{DA}} \vert \\[0.8em] &= \frac{1}{2} \cdot \left(\left| \textcolor{#cc071e}{\begin{pmatrix} 0 \\ 30 \\ 0 \end{pmatrix}} \right| + \left| \textcolor{#0087c1}{\begin{pmatrix} 0 \\ 14 \\ 0 \end{pmatrix}} \right|\right) \cdot \left| \textcolor{#e9b509}{\begin{pmatrix} 15 \\ 0 \\ -8 \end{pmatrix}} \right| \\[0.8em] &= \frac{1}{2} \cdot \left( \sqrt{0^2 + 30^2 + 0^2} + \sqrt{0^2 + 14^2 + 0^2} \right) \cdot \sqrt{15^2 + 0^2 + (-8)^2} \\[0.8em] &= \frac{1}{2} \cdot (30 + 14) \cdot 17 = 22 \cdot 17 = 374\end{align*}\]
2. Möglichkeit: Vektorprodukt anwenden (zeitaufwendiger)

Das Trapez \(ABCD\) kann in die beiden Dreiecke \(ABC\) und \(ACD\) zerlegt werden. Der Flächeninhalt eines Dreiecks lässt sich mithilfe des Vektorprodukts berechnen.
Anwendung des Vekorprodukts
Der Betrag des Vektorprodukts \(\overrightarrow{a} \times \overrightarrow{b}\) entspricht der Maßzahl des Flächeninhalts eines von zwei Vektoren \(\overrightarrow{a} \neq \overrightarrow{0}\) und \(\overrightarrow{b} \neq \overrightarrow{0}\) aufgespannten Parallelogramms.
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \textcolor{#cc071e}{\vert \overrightarrow{b} \vert \cdot \sin{\varphi}}\]
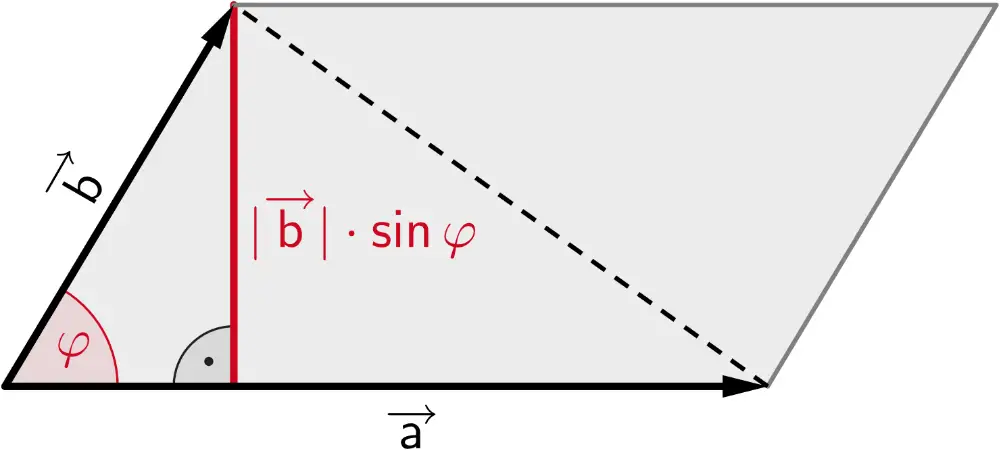
Flächeninhalt eines Parallelogramms
\[A = \vert \overrightarrow{a} \times \overrightarrow{b} \vert\]
Flächeninhalt eines Dreiecks
\[A = \frac{1}{2} \cdot \vert \overrightarrow{a} \times \overrightarrow{b} \vert\]
\(\textcolor{#cc071e}{\overrightarrow{AB}} = \textcolor{#cc071e}{\begin{pmatrix} 0 \\ 30 \\ 0 \end{pmatrix}}\), \(\textcolor{#0087c1}{\overrightarrow{DC}} = \textcolor{#0087c1}{\begin{pmatrix} 0 \\ 14 \\ 0 \end{pmatrix}}\), \(\textcolor{#e9b509}{\overrightarrow{DA}} = \textcolor{#e9b509}{\begin{pmatrix} 15 \\ 0 \\ -8 \end{pmatrix}}\) (vgl. Teilaufgabe a)
\[\textcolor{#89ba17}{\overrightarrow{AC}} = \overrightarrow{OC} - \overrightarrow{OA} = \begin{pmatrix} 2\\4\\8 \end{pmatrix} - \begin{pmatrix} 17 \\ -10 \\0 \end{pmatrix} = \textcolor{#89ba17}{\begin{pmatrix} -15 \\ 14 \\ 8 \end{pmatrix}}\]
Vektorprodukt (Kreuzprodukt)
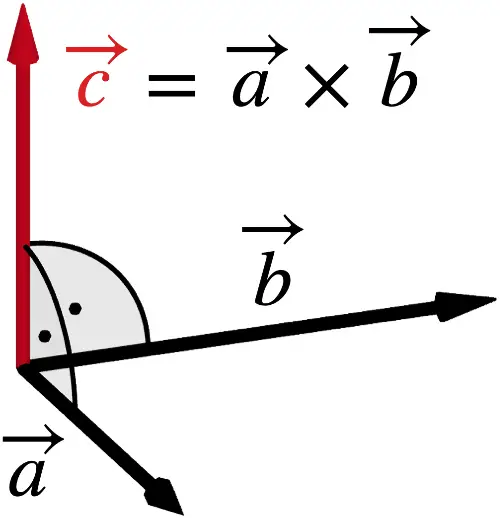
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\neq \overrightarrow{0}\) und \(\overrightarrow{b} \neq \overrightarrow{0}\), die nicht parallel zueinander sind, erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\), der zu beiden Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) orthogonal (senkrecht) ist.
\[\textcolor{#cc071e}{\overrightarrow{c}} = \overrightarrow{a} \times \overrightarrow{b} \, \Rightarrow \begin{cases}\textcolor{#cc071e}{\overrightarrow{c}} \circ \overrightarrow{a} = 0\; \Leftrightarrow \;\textcolor{#cc071e}{\overrightarrow{c}} \perp \overrightarrow{a} \\\textcolor{#cc071e}{\overrightarrow{c}} \circ \overrightarrow{b} = 0\; \Leftrightarrow \;\textcolor{#cc071e}{\overrightarrow{c}} \perp \overrightarrow{b}\end{cases} \quad (\overrightarrow{a} \neq \overrightarrow{0},\, \overrightarrow{b} \neq \overrightarrow{0},\, \overrightarrow{a} \neq k \cdot \overrightarrow{b}\;\text{mit} \;k \in \mathbb R \backslash \{0\})\]
Es gilt: \(\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\)
\(\overrightarrow{a} \times \overrightarrow{b} = -\left(\overrightarrow{b} \times \overrightarrow{a}\right)\)
(Das Kommutativgesetz gilt nicht.)
Die Rechte-Hand-Regel beschreibt die gegenseitige Lage der Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\textcolor{#cc071e}{\overrightarrow{c}} = \overrightarrow{a} \times \overrightarrow{b}\) im Raum. Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, so weist der Mittelfinger in Richtung von \(\textcolor{#cc071e}{\overrightarrow{c}} = \overrightarrow{a} \times \overrightarrow{b}\).

\[\begin{align*} A_{ABCD} &= A_{ABC} + A_{ACD} \\[0.8em] &= \frac{1}{2} \cdot \vert \textcolor{#cc071e}{\overrightarrow{AB}} \times \textcolor{#89ba17}{\overrightarrow{AC}} \vert + \frac{1}{2} \cdot \vert \textcolor{#e9b509}{\overrightarrow{DA}} \times \textcolor{#0087c1}{\overrightarrow{DC}} \vert \\[0.8em] &= \frac{1}{2} \cdot \left| \textcolor{#cc071e}{\begin{pmatrix} 0 \\ 30 \\ 0 \end{pmatrix}} \times \textcolor{#89ba17}{\begin{pmatrix} -15 \\ 14 \\ 8 \end{pmatrix}} \right| + \frac{1}{2} \cdot \left| \textcolor{#e9b509}{\begin{pmatrix} 15 \\ 0 \\ -8 \end{pmatrix}} \times \textcolor{#0087c1}{\begin{pmatrix} 0 \\ 14 \\ 0 \end{pmatrix}} \right| \\[0.8em] &= \frac{1}{2} \cdot \left| \begin{pmatrix} 30 & \cdot & 8 & - & 0 & \cdot & 14 \\ 0 & \cdot & (-15) & - & 0 & \cdot & 8 \\ 0 & \cdot & 14 & - & 30 & \cdot & (-15) \end{pmatrix} \right| + \frac{1}{2} \cdot \left| \begin{pmatrix} 0& \cdot & 0 & - & (-8) & \cdot & 14 \\ -8 & \cdot & 0 & - & 15 & \cdot & 0 \\ 15 & \cdot & 14 & - & 0 & \cdot & 0 \end{pmatrix} \right| \\[0.8em] &= \frac{1}{2} \cdot \left| \begin{pmatrix} 240 \\ 0 \\ 450 \end{pmatrix} \right| + \frac{1}{2} \cdot \left| \begin{pmatrix}112 \\ 0 \\ 210 \end{pmatrix} \right| \\[0.8em] &= \frac{1}{2} \cdot \sqrt{240^2 + 0^2 + 450^2} + \frac{1}{2} \cdot \sqrt{112^2 + 0^2 + 210^2} \\[0.8em] &= \frac{1}{2} \cdot 510 + \frac{1}{2} \cdot 238 \\[0.8em] &= 255 + 119 \\[0.8em] &= 374 \end{align*}\]
(Vgl. Mathematik Abiturskript Bayern G9 - 3 Geometrie, 3.2.1 Rechnen mit Vektoren - Betrag eines Vektors, 3.2.3 Vektorprodukt zweier Vektoren)


