Bestimmen Sie nun mithilfe des Graphen von \(\boldsymbol{F}\) aus Aufgabe 2c den Flächeninhalt der gesamten Vorderseite der Dachgaube (einschließlich des Fensters).
Beschreiben Sie unter Einbeziehung dieses Flächeninhalts die wesentlichen Schritte eines Lösungswegs, mit dem der Wert von \(a\) rechnerisch so bestimmt werden könnte, dass bei einer Fensterhöhe von 1,50 m der Teil der Vorderseite der Dachgaube, der in Abbildung 3 schraffiert dargestellt ist, den Flächeninhalt 6 m2 hat.
(5 BE)
Lösung zu Teilaufgabe 2d
Flächeninhalt der gesamten Vorderseite der Dachgaube
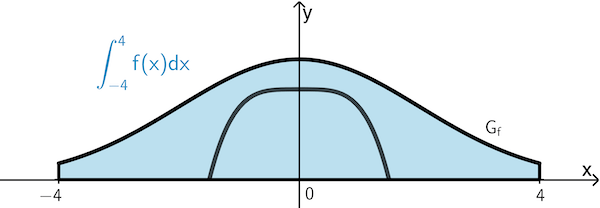
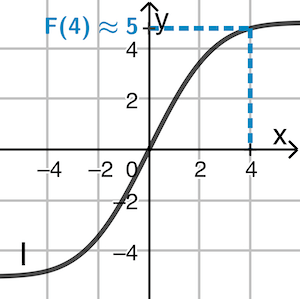
Graph I zeigt den Verlauf einer Stammfunktion \(F\) von \(f\) (vgl. Teilaufgabe 2c), womit sich der Flächeninhalt der Vorderseite der Dachgaube näherungsweise durch Integration berechnen lässt.
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*}A_{\text{Vorderseite}} &= \textcolor{#0087c1}{\int_{-4}^4 f(x)dx} = 2 \cdot \int_0^4 f(x)dx \\[0.8em] &= 2 \cdot (\textcolor{#0087c1}{F(4)} - F(0)) \approx 2 \cdot (\textcolor{#0087c1}{5} - 0) = 10\end{align*}\]
Beschreibung eines rechnerischen Lösungswegs für die Bestimmung von \(a\)
Mögliche Abfolge wesentlicher Schritte (ohne Skizzen):
1. Schritt: Flächeninhalt des Fensters berechnen
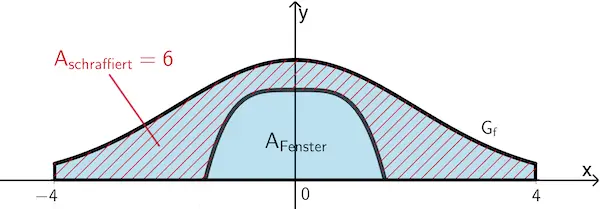
\(A_{\text{Fenster}} = \textcolor{#0087c1}{A_{\text{Vorderseite}}} - \textcolor{#cc071e}{A_{\text{schraffiert}}} = \textcolor{#0087c1}{10} - \textcolor{#cc071e}{6} = 4\) (vgl. oben bzw. Angabe)
2. Schritt: Nullstellen der Funktion \(\boldsymbol{g}\) bestimmen
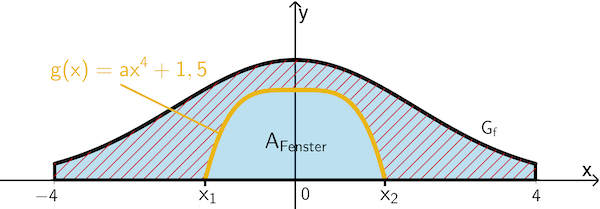
\(\textcolor{#e9b509}{g(x)} = 0 \; \Leftrightarrow \; \textcolor{#e9b509}{ax^4 + 1{,}5} = 0 \; \Rightarrow x_1, x_2\) mit \(x_1 < x_2\)
Ergänzende Erklärung (nicht verlangt)
Der Wert des Parameters \(b\) der Funktion \(g\) mit \(g(x) = ax^4 + b\) legt im Modell für \(b > 0\) die Höhe des Fensters fest (vgl. Teilaufgabe 2b). Bei einer Fensterhöhe von 1,50 m (vgl. Angabe) gilt \(b = 1{,}5\) und damit \(\textcolor{#e9b509}{g(x) = ax^4 + 1{,}5}\).
\(x_1\) und \(x_2\) sind die Nullstellen von \(g\) in Abhängigkeit des Parameters \(a\). Sie liefern die Integrationsgrenzen für die Berechnung des Flächeninhalts der Fensterfläche in Abhängigkeit des Parameters \(a\) durch Integration (vgl. 3. Schritt). Mit \(x_ 1 < x_2\) ist \(x_1\) die untere und \(x_2\) die obere Integrationsgrenze.
3. Schritt: Lösungsansatz für die Bestimmung von \(\boldsymbol{a}\) formulieren
\(\displaystyle \int_{x_1}^{x_2}\textcolor{#e9b509}{(ax^4 + 1{,}5)}\,dx = 4 \; \Rightarrow \; a\) mit \(a < 0\)
Ergänzende Erklärung (nicht verlangt)
Das bestimmte Integral \(\displaystyle \int_{x_1}^{x_2}\textcolor{#e9b509}{(ax^4 + 1{,}5)}\,dx\) beschreibt den Flächeninhalt des Fensters in Abhängigkeit des Parameters \(a\). Da der Flächeninhalt des Fensters aus Schritt 1 mit 4 m² bekannt ist, liefert die Gleichung \(\displaystyle \int_{x_1}^{x_2}\textcolor{#e9b509}{(ax^4 + 1{,}5)}\,dx = 4 \) einen Lösungsansatz für die Bestimmung des Werts des Parameters \(a\), wobei \(a < 0\) gilt (vgl. Teilaufgabe 2b).


