Skizzieren Sie den Graphen der Funktion \(A\) unter Verwendung der bisherigen Ergebnisse in der Abbildung 2.
(3 BE)
Lösung zu Teilaufgabe 2e
Bisherige Ergebnisse:
- \(A(0) = 1\) (vgl. Teilaufgabe 2a)
- Steigung der Tangente im Punkt \((0|1)\): \(\textcolor{#cc071e}{A'(0) = 0{,}175}\) (vgl. Teilaufgabe 2c)
- \(\textcolor{#e9b509}{\lim \limits_{x\,\to\,+\infty} A(x) = 8}\) (vgl. Teilaufgabe 2a)
- \(G_{A}\) ist streng monoton steigend (vgl. Teilaufgabe 2a).
- Der Punkt \((x_{0}|4)\) mit \(x_{0} \approx 9{,}7\) ist Wendepunkt von \(G_{A}\) (vgl. Teilaufgabe 2b,d).
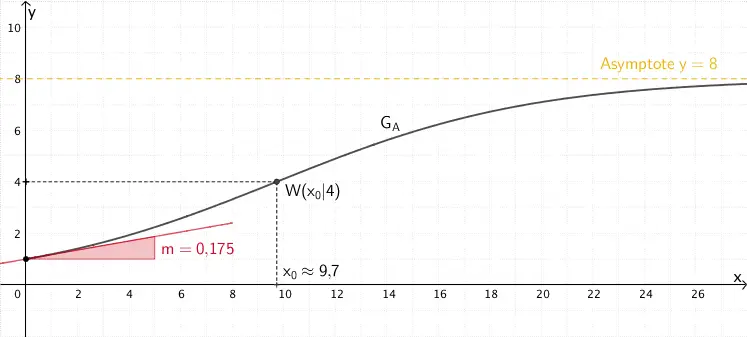
Graph der in \(\mathbb R_{0}^{+}\) definierten Funktion \(A \colon x \mapsto \dfrac{8}{f(x)}\) mit \(f(x) = 1 + 7e^{-0{,}2x}\).


