Abbildung 1 zeigt eine Sonnenuhr mit einer gegenüber der Horizontalen geneigten, rechteckigen Grundplatte, auf der sich ein kreisförmiges Zifferblatt befindet. Auf der Grundplatte ist der Polstab befestigt, dessen Schatten bei Sonneneinstrahlung die Uhrzeit auf dem Zifferblatt anzeigt.
 Abb. 1
Abb. 1
Eine Sonnenuhr dieser Bauart wird in einem kartesischen Koordinatensystem modellhaft dargestellt (vgl. Abbildung 2). Dabei beschreibt das Rechteck \(ABCD\) mit \(A\,(5|-4|0)\) und \(B\,(5|4|0)\) die Grundplatte der Sonnenuhr. Der Befestigungspunkt des Polstabs auf der Grundplatte wird im Modell durch den Diagonalenschnittpunkt \(M\,(2{,}5|0|2)\) des Rechtecks \(ABCD\) dargestellt. Eine Längeneinheit im Koordinatensystem entspricht 10 cm in der Realität. Die Horizontale wird im Modell durch die \(x_{1}x_{2}\)-Ebene beschrieben.
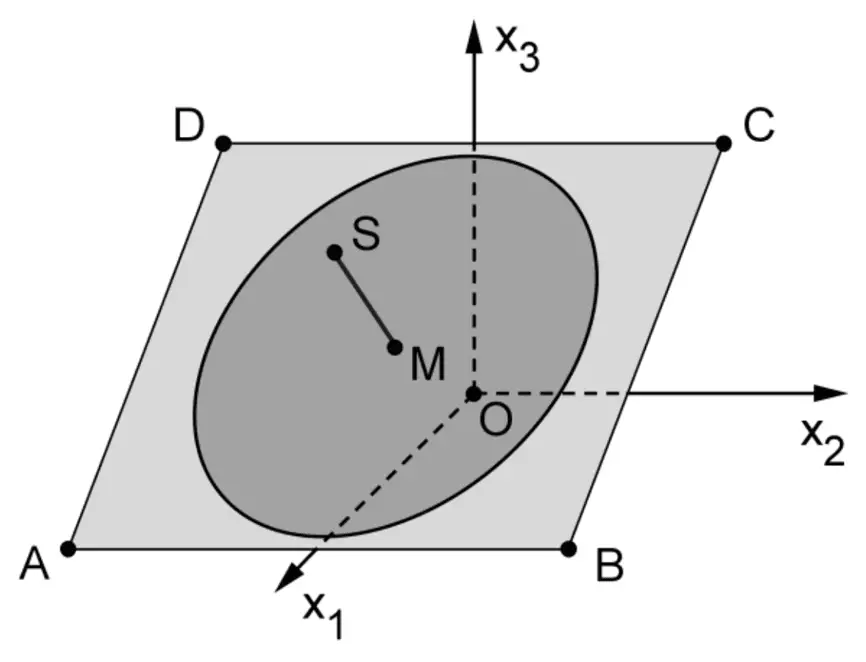 Abb. 2
Abb. 2
Bestimmen Sie die Koordinaten des Punkts \(C\). Ermitteln Sie eine Gleichung der Ebene \(E\), in der das Rechteck \(ABCD\) liegt, in Normalenform.
(mögliches Teilergebnis: \(E\colon 4x_{1} + 5x_{3} - 20 = 0\))
(5 BE)
Lösung zu Teilaufgabe a
Vektoraddition, Ebenengleichung in Normalenform
\[A\,(5|-4|0)\,, \enspace B\,(5|4|0)\,, \enspace M\,(2{,}5|0|2)\]
Koordinaten des Punktes \(C\)
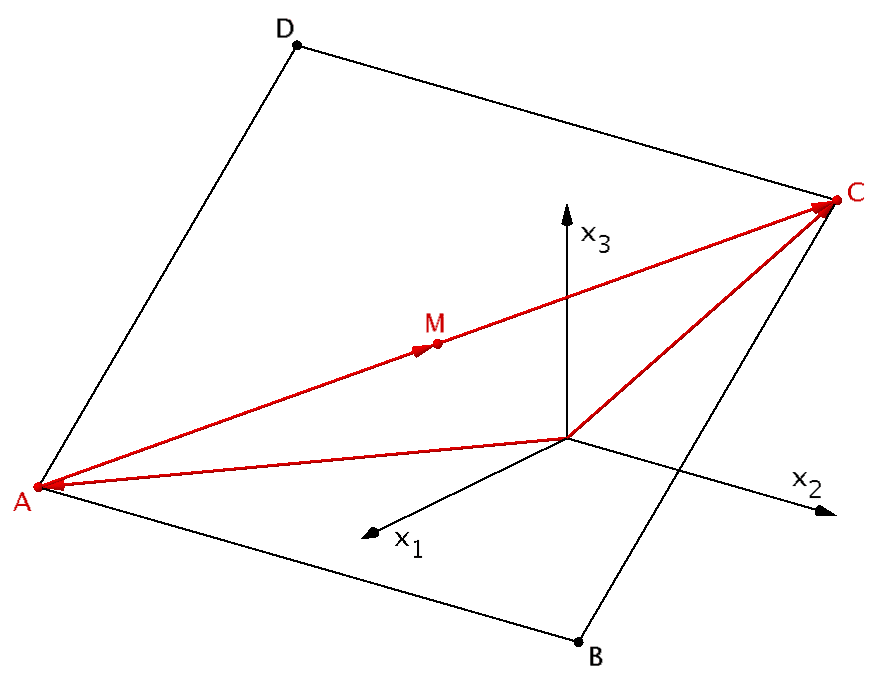
Vektoraddition zur Berechnung der Koordinaten des Punktes \(C\)
\[A\,(5|-4|0)\,, \enspace M\,(2{,}5|0|2)\]
\[\begin{align*} \overrightarrow{C} &= \overrightarrow{A} + 2 \cdot \overrightarrow{AM} \\[0.8em] &= \overrightarrow{A} + 2 \cdot (\overrightarrow{M} - \overrightarrow{A}) \\[0.8em] &= \begin{pmatrix} 5 \\ -4 \\ 0 \end{pmatrix} + 2 \cdot \left[ \begin{pmatrix} 2{,}5 \\ 0 \\ 2 \end{pmatrix} - \begin{pmatrix} 5 \\ -4 \\ 0 \end{pmatrix} \right] \\[0.8em] &= \begin{pmatrix} 5 \\ -4 \\ 0 \end{pmatrix} + 2 \cdot \begin{pmatrix} -2{,}5 \\ 4 \\ 2 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 0 \\ 4 \\ 4 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad C\,(0|4|4)\]
Gleichung der Ebene \(E\) in Normalenform
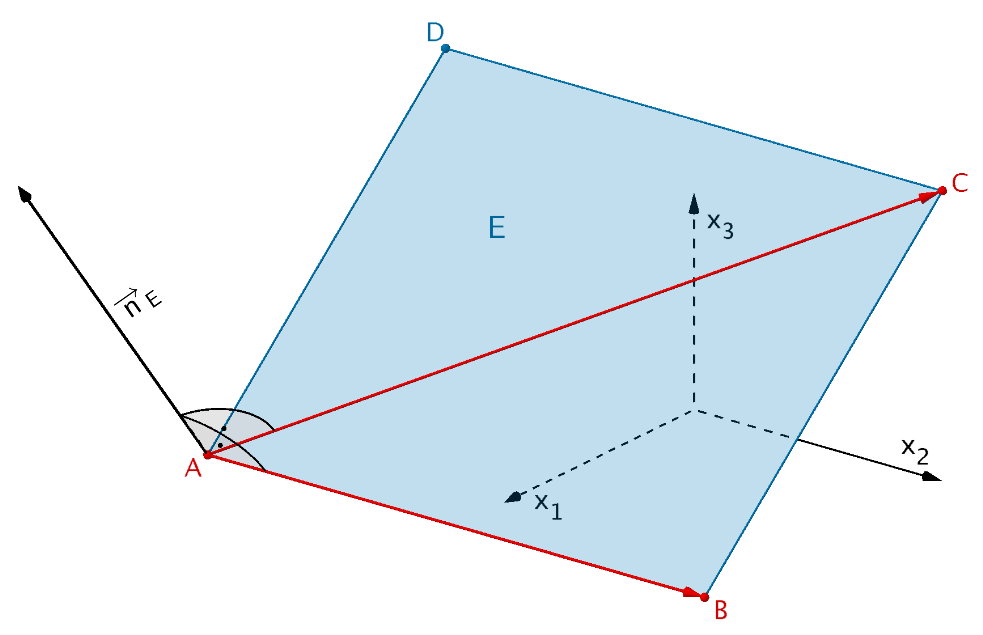
Das Rechteck \(ABCD\) liegt in der Ebene \(E\). Die Ebene \(E\) lässt sich z.B. durch die beiden linear unabhängigen Vektoren \(\overrightarrow{AB}\) und \(\overrightarrow{AC}\) sowie dem Aufpunkt \(A\) beschreiben.
Mithilfe des Vektorprodukts aus dem Vektor \(\overrightarrow{AB}\) und dem Vektor \(\overrightarrow{AC}\) bestimmt man den Normalenvektor \(\overrightarrow{n}_{E}\) für die Gleichung der Ebene \(E\) in Normalenform.
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jede Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
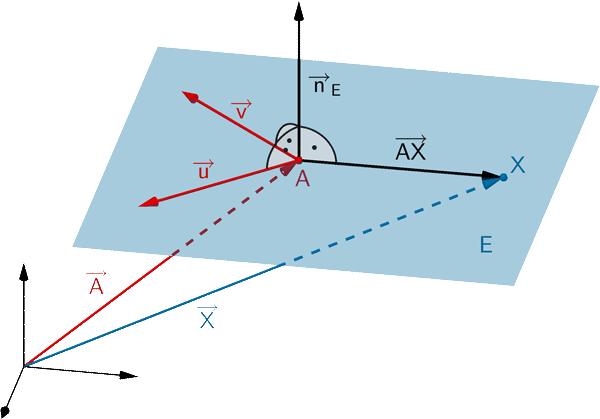
Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) bestimmen:
Vektorprodukt (Kreuzprodukt)
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) mit den Eigenschaften:
\(\overrightarrow{c}\) ist sowohl zu \(\overrightarrow{a}\) als auch zu \(\overrightarrow{b}\) senkrecht.
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist gleich dem Produkt aus den Beträgen der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) und dem Sinus des von ihnen eingeschlossenen Winkels \(\varphi\).
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, dann weist \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) in Richtung des Mittelfingers.
Berechnung eines Vektorprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\]
\[A\,(5|-4|0)\,, \enspace B\,(5|4|0)\,, \enspace C\,(0|4|4)\]
\[\begin{align*} \overrightarrow{AB} \times \overrightarrow{AC} &= (\overrightarrow{B} - \overrightarrow{A}) \times (\overrightarrow{C} - \overrightarrow{A}) \\[0.8em] &= \left[ \begin{pmatrix} 5 \\ 4 \\ 0 \end{pmatrix} - \begin{pmatrix} 5 \\ -4 \\ 0 \end{pmatrix} \right] \times \left[ \begin{pmatrix} 0 \\ 4 \\ 4 \end{pmatrix} - \begin{pmatrix} 5 \\ -4 \\ 0 \end{pmatrix} \right] \\[0.8em] &= \begin{pmatrix} 0 \\ 8 \\ 0 \end{pmatrix} \times \begin{pmatrix} -5 \\ 8 \\ 4 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 8 & \cdot & 4 & - & 0 & \cdot & 8 \\ 0 & \cdot & (-5) & - & 0 & \cdot & 4 \\ 0 & \cdot & 8 & - & 8 & \cdot & (-5) \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 32 \\ 0 \\ 40 \end{pmatrix} \\[0.8em] &= 8 \cdot \begin{pmatrix} 4 \\ 0 \\ 5 \end{pmatrix} \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 4 \\ 0 \\ 5 \end{pmatrix}\]
Gleichung der Ebene \(E\) in Normalenform aufstellen:
Der Ansatz für die Gleichung der Ebene \(E\) kann mit der Normalenform in Vektordarstellung oder in Koordinatendarstellung erfolgen.
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jede Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]

Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
Ansatz mit der Normalenform in Vektordarstellung:
\[A\,(5|-4|0)\,, \enspace \overrightarrow{n}_{E} = \begin{pmatrix} 4 \\ 0 \\ 5 \end{pmatrix}\]
\[E\colon \overrightarrow{n}_{E} \circ \left( \overrightarrow{X} - \overrightarrow{A} \right) = 0\]
\[\begin{align*} \begin{pmatrix} 4 \\ 0 \\ 5 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 5 \\ -4 \\ 0 \end{pmatrix} \right] &= 0 \\[0.8em] 4 \cdot (x_{1} - 5) + 0 \cdot (x_{2} + 4) + 5 \cdot (x_{3} - 0) &= 0 \\[0.8em] 4x_{1} + 5x_{3} - 20 &= 0 \end{align*}\]
\[E\colon 4x_{1} + 5x_{3} - 20 = 0\]
Ansatz mit der Normalenorm in Koordiantendarstellung:
\[A\,(5|-4|0)\,, \enspace \overrightarrow{n}_{E} = \begin{pmatrix} 4 \\ 0 \\ 5 \end{pmatrix}\]
\[\begin{align*} E\colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} &= 0 \\[0.8em] 4x_{1} + 5x_{3} + n_{0} &= 0 \end{align*}\]
\[\begin{align*} A \in E\colon 4 \cdot 5 + 5 \cdot 0 + n_{0} &= 0 \\[0.8em] 20 + n_{0} &= 0 & &| - 20 \\[0.8em] n_{0} &= -20 \end{align*}\]
\[E\colon 4x_{1} + 5x_{3} - 20 = 0\]


