Der Punkt \((0|0|h)\) liegt innerhalb des Quaders und hat von den drei Strecken \([AB]\), \([BC]\) und \([CD]\) den gleichen Abstand. Das folgende Gleichungssystem liefert den Wert von \(h\):
\[\textsf{I}\quad \overrightarrow{Q} = \begin{pmatrix} 11 \\ 11 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} -22 \\ 0 \\ 28 \end{pmatrix}, \; t \in [0;1]\]
\[\textsf{II}\quad \overrightarrow{PQ} \circ \overrightarrow{AB} = 0\]
\[\textsf{III}\quad \overline{PQ} = 28 - h\]
Erläutern Sie die Überlegungen, die diesem Vorgehen zur Bestimmung des Werts von \(h\) zugrunde liegen.
(4 BE)
Lösung zu Teilaufgabe g
Gleichung I beschreibt einen Punkt \(Q\) auf der Strecke \([AB]\).
Gleichung II formuliert die Bedingung \([PQ] \perp [AB]\) für den Abstand des Punktes \(P\) von der Strecke \([AB]\).
Gleichung III legt fest, dass der Abstand \(\overline{PQ}\) des Punktes \(P\) von der Strecke \([AB]\) gleich dem Abstand \(28 - h\) des Punktes \(P\) von der Strecke \([BC]\) ist.
Ausführliche Erklärung (nicht verlangt)
Gleichung einer Gerade / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
![Punkt Q auf der Strecke [AB]](/images/stories/B2022_PT_B_G2/B2022_PT_B_G2_g_1.png)
\[\textsf{I}\quad \textcolor{#cc071e}{\overrightarrow{Q}} = \textcolor{#cc071e}{\begin{pmatrix} 11 \\ 11 \\ 0 \end{pmatrix}} + t \cdot \textcolor{#cc071e}{\begin{pmatrix} -22 \\ 0 \\ 28 \end{pmatrix}}, \; \textcolor{#cc071e}{t \in [0;1]}\]
Gleichung I beschreibt einen Punkt \(\textcolor{#cc071e}{Q}\) auf der Strecke \(\textcolor{#cc071e}{[AB]}\) in der Parameterform.
Dabei ist \(\textcolor{#cc071e}{A(11|11|0)}\) der Aufpunkt und \(\textcolor{#cc071e}{\overrightarrow{AB}} = \begin{pmatrix} -11 \\ 11\\ 28 \end{pmatrix} - \begin{pmatrix} 11 \\ 11\\ 0 \end{pmatrix} = \textcolor{#cc071e}{\begin{pmatrix} -22 \\ 0 \\ 28 \end{pmatrix}}\) ein Richtungsvektor.
Entscheidend ist die Einschränkung \(\textcolor{#cc071e}{t \in [0;1]}\), welche die Strecke \(\textcolor{#cc071e}{[AB]}\) festlegt (\(t \in \mathbb R\) würde die Gerade \(AB\) festlegen).
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \; \Leftrightarrow \; \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\[\textsf{II}\quad \textcolor{#0087c1}{\overrightarrow{PQ}} \circ \textcolor{#cc071e}{\overrightarrow{AB}} = 0\]
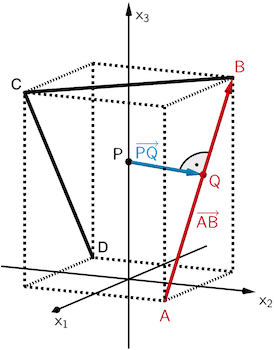
Gleichung II formuliert das Skalarprodukt der zueinander senkrechten Verbindungsvektoren \(\textcolor{#cc071e}{\overrightarrow{AB}}\) und \(\textcolor{#0087c1}{\overrightarrow{PQ}}\), denn es gilt:
\[\textcolor{#0087c1}{\overrightarrow{PQ}} \circ \textcolor{#cc071e}{\overrightarrow{AB}} = 0 \enspace \Leftrightarrow \enspace \textcolor{#0087c1}{\overrightarrow{PQ}} \perp \textcolor{#cc071e}{\overrightarrow{AB}}\]
\[\Rightarrow \enspace \textcolor{#0087c1}{[PQ]} \perp \textcolor{#cc071e}{[AB]}\]
Damit legt die Gleichung die Bedingung dafür fest, dass \(\textcolor{#0087c1}{\overline{PQ}}\) der Abstand des Punktes \(P\) von der Strecke \(\textcolor{#cc071e}{[AB]}\) ist.
![Abstand des Punktes P von der Strecke [AB] sowie von der Strecke [BC]](/images/stories/B2022_PT_B_G2/B2022_PT_B_G2_g_3.png)
\[\textsf{III}\quad \textcolor{#0087c1}{\overline{PQ}} = \textcolor{#89ba17}{28 - h}\]
Gleichung III legt fest, dass der Punkt \(P(0|0|\textcolor{#e9b509}{h})\) von den Strecken \(\textcolor{#cc071e}{[AB]}\) und \([BC]\) den gleichen Abstand hat.
\(\textcolor{#0087c1}{\overline{PQ}}\) ist der Abstand des Punktes \(P\) von der Strecke \(\textcolor{#cc071e}{[AB]}\) (vgl. Gleichung II).
Der Punkt \(P(0|0|\textcolor{#e9b509}{h})\) liegt auf der \(x_3\)-Achse, welche die Strecke \([BC]\) rechtwinklig schneidet.
Da die Höhe des Quaders \(28\) beträgt (vgl. \(x_3\)-Koordinate von \(B\) und \(C\)), beschreibt der Term \(\textcolor{#89ba17}{28 - h}\) den Abstand des Punktes \(P\) von der Strecke \([BC]\).


