- Details
- Kategorie: Analysis 1
Gegeben ist die Funktion \(f \colon x \mapsto \dfrac{x^2 + 2x}{x+1}\) mit maximaler Definitionsmenge \(D_f\). Geben Sie \(D_f\) und die Nullstellen von \(f\) an.
(2 BE)
- Details
- Kategorie: Analysis 1
Geben Sie einen Term einer gebrochen-rationalen Funktion an, die die folgenden Eigenschaften hat: Die Funktion \(h\) ist in \(\mathbb R\) definiert; ihr Graph besitzt die Gerade mit der Gleichung \(y = 3\) als waagrechte Asymptote und schneidet die \(y\)-Achse im Punkt \((0|4)\).
(3 BE)
- Details
- Kategorie: Analysis 1
Gegeben ist die in \(\mathbb R^+\) definierte Funktion \(g \colon x \mapsto \dfrac{4}{x}\). Abbildung 1 zeigt den Graphen von \(g\).
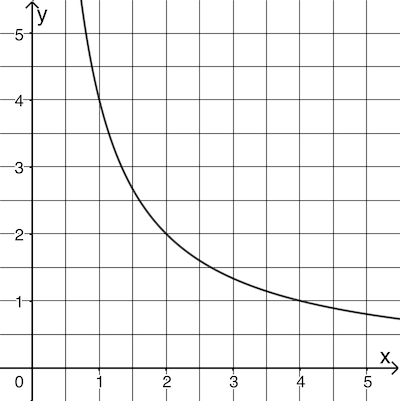Abb. 1
Berechnen Sie den Wert des Integrals \(\displaystyle \int_1^e g(x)dx\).
(2 BE)
- Details
- Kategorie: Analysis 1
Ermitteln Sie grafisch diejenige Stelle \(x_0 \in \mathbb R^+\), für die gilt: Die lokale Änderungsrate von \(g\) an der Stelle \(x_0\) stimmt mit der mittleren Änderungsrate von \(g\) im Intervall \([1;4]\) überein.
(3 BE)
- Details
- Kategorie: Analysis 1
Der Graph \(G_f\) der in \(\mathbb R\) definierten ganzrationalen Funktion \(f\) besitzt nur an der Stelle \(x = 3\) eine waagrechte Tangente (vgl. Abbildung 2).
Betrachtet wird die in \(\mathbb R\) definierte Funktion \(g\) mit \(g(x) = f\left(f(x)\right)\).
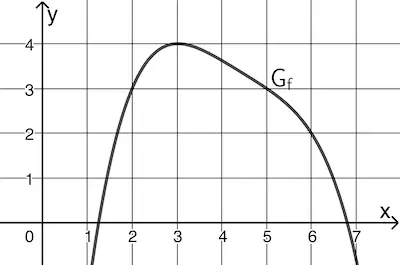Abb. 2
Geben Sie mithilfe von Abbildung 2 die Funktionswerte \(f(6)\) und \(g(6)\) an.
(2 BE)
- Details
- Kategorie: Analysis 1
Gemäß der Kettenregel gilt \(g'(x) = f'\left( f(x) \right) \cdot f'(x)\). Ermitteln Sie damit und mithilfe von Abbildung 2 alle Stellen, an denen der Graph von \(g\) eine waagrechte Tangente besitzt.
(3 BE)
- Details
- Kategorie: Analysis 1
Gegeben sind die in \(\mathbb R\) definierten Funktionen \(f_a\) mit \(f_a(x) = a \cdot e^{-x} + 3\) und \(a \in \mathbb R \backslash \{0\}\).
Zeigen Sie, dass \(f'_a(0) = -a\) gilt.
(1 BE)
- Details
- Kategorie: Analysis 1
Betrachtet wird die Tangente an den Graphen von \(f_a\) im Punkt \((0|f_a (0))\). Bestimmen Sie diejenigen Werte von \(a\), für die diese Tangente eine positive Steigung hat und zudem die \(x\)-Achse in einem Punkt schneidet, dessen \(x\)-Koordinate größer als \(\dfrac{1}{2}\) ist.
(4 BE)
