Abbildung 1 zeigt den Körper \(ABCDEFGH\), bei dem die quadratische Grundfläche \(ABCD\) parallel zur quadratischen Deckfläche \(EFGH\) liegt. Der Körper ist symmetrisch sowohl bezüglich der \(x_1x_3\)-Ebene als auch bezüglich der \(x_2x_3\)-Ebene. Außerdem werden die Punkte \(S_k(0|0|k)\) mit \(k \in \; ]7;+\infty[\) betrachtet, die Spitzen von Pyramiden \(EFGHS_k\) sind.
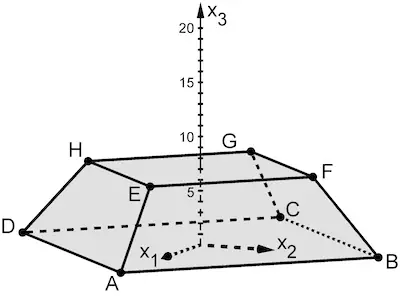Abb. 1
Bestimmen Sie rechnerisch denjenigen Wert von \(k\), für den die Pyramide \(EFGHS_k\) den Körper \(ABCDEFGH\) zu einer großen Pyramide \(ABCDS_k\) ergänzt.
(zur Kontrolle: \(k = 19\))
(2 BE)
Lösung zu Teilaufgabe c
\[S_k(0|0|k) \in L\colon 0 + 0 + k - 19 = 0 \; \Rightarrow \; k = 19\]
oder
\[S_k \in AE \colon \begin{pmatrix} 0\\0\\k \end{pmatrix} = \begin{pmatrix} 19\\0\\0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -7\\0\\7 \end{pmatrix}\]
\[\begin{align*} \text{I} & & & 0 = 19 - 7\lambda \; \Rightarrow \; \lambda = \frac{19}{7} \\[0.8em] \text{II} & & \wedge \enspace & 0 = 0 \\[0.8em] \text{III} & & \wedge \enspace & k = 7\lambda \end{align*}\]
Gleichung \(\text{III}\): \(k = 7 \cdot \dfrac{19}{7} = 19\)
Ausführliche Erklärung (nicht verlangt)
1. Möglichkeit: Seitenfläche \(\boldsymbol{ABS_k}\) betrachten
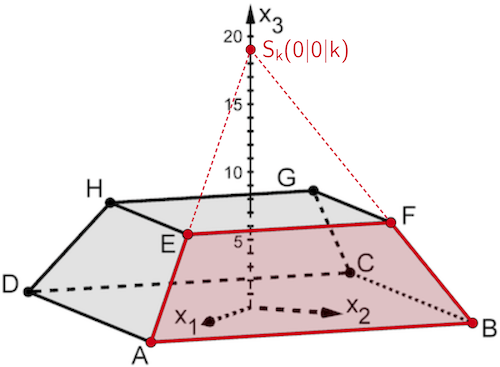Abb. 1
Planskizze (optional): Das Trapez \(\textcolor{#cc071e}{ABEF}\) liegt in der Ebene \(L\) (vgl. Teilaufgabe b) und ist Teil der Seitenfläche \(\textcolor{#cc071e}{ABS_k}\) der großen Pyramide \(ABCDS_k\). Die Spitze \(\textcolor{#cc071e}{S_k}\) liegt somit in der Ebene \(L\).
\[L\colon x_1 + x_2 + x_3 - 19 = 0\]
\[\begin{align*}\textcolor{#cc071e}{S_k(0|0|k)} \in L\colon \textcolor{#cc071e}{0} + \textcolor{#cc071e}{0} + \textcolor{#cc071e}{k} - 19 &= 0 &&| + 19 \\[0.8em] k &= 19\end{align*}\]
Für \(k = 19\), ergänzt die Pyramide \(EFGHS_{19}\) den Körper \(ABCDEFGH\) zu einer großen Pyramide \(ABCDS_{19}\).
2. Möglichkeit: Z. B. Seitenkante \(\boldsymbol{AS_k}\) betrachten
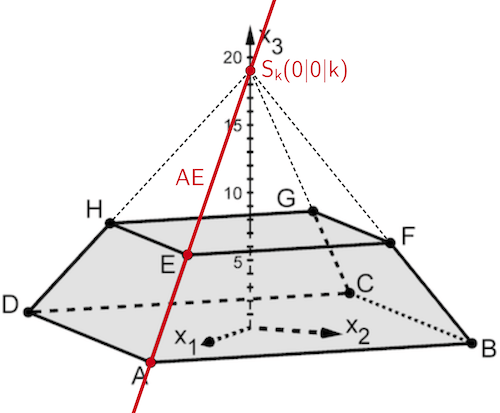Abb. 1
Planskizze (optional): Die Seitenkante \(\textcolor{#cc071e}{[ES_k]}\) der Pyramide \(EFGHS_k\) ergänzt die Seitenkante \(\textcolor{#cc071e}{[AE]}\) des Körpers \(ABCDEFGH\) zur Seitenkante \(\textcolor{}{[AS_k]}\) der großen Pyramide \(ABCDS_k\). Die Spitze \(\textcolor{#cc071e}{S_k}\) liegt daher auf der Gerade \(\textcolor{#cc071e}{AE}\).
Gleichung der Gerade \(\textcolor{#cc071e}{AE}\) in Parameterform:
Gleichung einer Gerad / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
\(A(19|0|0)\), \(\overrightarrow{AE} = \begin{pmatrix} -7\\0\\7 \end{pmatrix}\) (vgl. Teilaufgabe a)
\[\textcolor{#cc071e}{AE} \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AE}; \; \lambda \in \mathbb R\]
\[\textcolor{#cc071e}{AE} \colon \overrightarrow{X} = \begin{pmatrix} 19\\0\\0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -7\\0\\7 \end{pmatrix}; \; \lambda \in \mathbb R\]
Wert von \(k\) bestimmen:
\[\textcolor{#cc071e}{S_k} \in \textcolor{#cc071e}{AE} \colon \textcolor{#cc071e}{\begin{pmatrix} 0\\0\\k \end{pmatrix}} = \begin{pmatrix} 19\\0\\0 \end{pmatrix} + \lambda \cdot \begin{pmatrix} -7\\0\\7 \end{pmatrix}\]
Koordinatenweise gelesen ergibt die Vektorgleichung folgendes Gleichungssystem:
\[\begin{align*} \text{I} & & & 0 = 19 - 7\lambda \\[0.8em] \text{II} & & \wedge \enspace & 0 = 0 \\[0.8em] \text{III} & & \wedge \enspace & k = 7\lambda \end{align*}\]
Aus Gleichung \(\text{I}\) folgt: \(\lambda = \dfrac{19}{7}\)
In Gleichung \(\text{III}\) eingesetzt: \(k = 7 \cdot \dfrac{19}{7} = 19\)
Für \(k = 19\), ergänzt die Pyramide \(EFGHS_{19}\) den Körper \(ABCDEFGH\) zu einer großen Pyramide \(ABCDS_{19}\).
