- Details
- Kategorie: Analysis 2
Geben Sie jeweils den Term einer in \(\mathbb R\) definierten periodischen Funktion an, die die angegebene Eigenschaft hat.
Der Graph der Funktion \(g\) geht aus dem Graphen der in \(\mathbb R\) definierten Funktion \(x \mapsto \sin x\) durch Spiegelung an der y-Achse hervor.
(1 BE)
- Details
- Kategorie: Analysis 2
Gegeben ist die in \(\mathbb R\) definierte Funktion \(f\) mit \(f(x) = e^x \cdot \left( 2x + x^2 \right)\).
Bestimmen Sie die Nullstellen der Funktion \(f\).
(2 BE)
- Details
- Kategorie: Analysis 2
Zeigen Sie, dass die in \(\mathbb R\) definierte Funktion \(F\) mit \(F(x) = x^2 \cdot e^x\) eine Stammfunktion von \(f\) ist. Geben eine Gleichung einer weiteren Stammfunktion \(G\) von \(f\) an, für die \(G(1) = 2e\) gilt.
(3 BE)
- Details
- Kategorie: Analysis 2
Der Graph einer in \(\mathbb R\) definierten Funktion \(g \, \colon \mapsto g(x)\) besitzt für \(-5 \leq x \leq 5\) zwei Wendepunkte. Entscheiden Sie, welcher der Graphen I, II und III zur zweiten Ableitungsfunktion \(g''\) von \(g\) gehört. Begründen Sie Ihre Entscheidung.
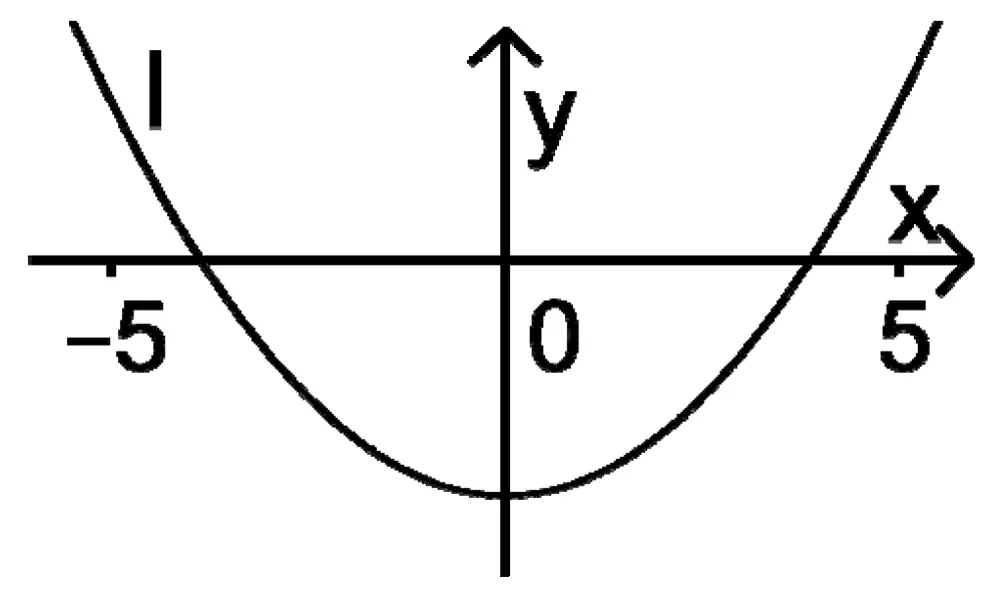
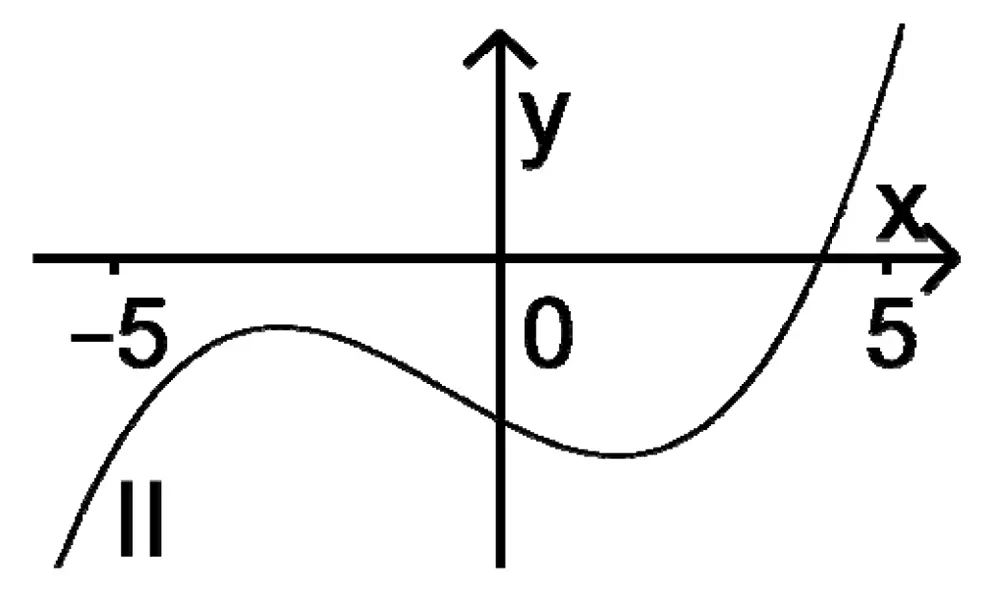
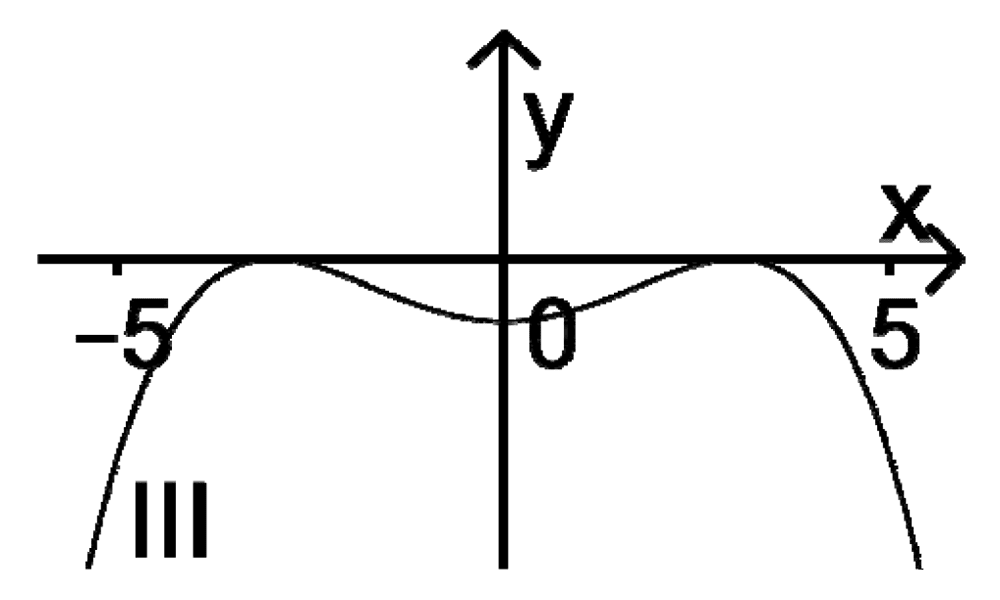
(2 BE)
- Details
- Kategorie: Analysis 2
In einem Koordinatensystem (vgl. Abbildung 1) werden alle Rechtecke betrachtet, die folgende Bedingungen erfüllen:
-
Zwei Seiten liegen auf den Koordinatenachsen.
-
Ein Eckpunkt liegt auf dem Graphen \(G_f\) der Funktion \(f \, \colon x \mapsto -\ln x\) mit \(0 < x < 1\).
Abbildung 1 zeigt ein solches Rechteck.
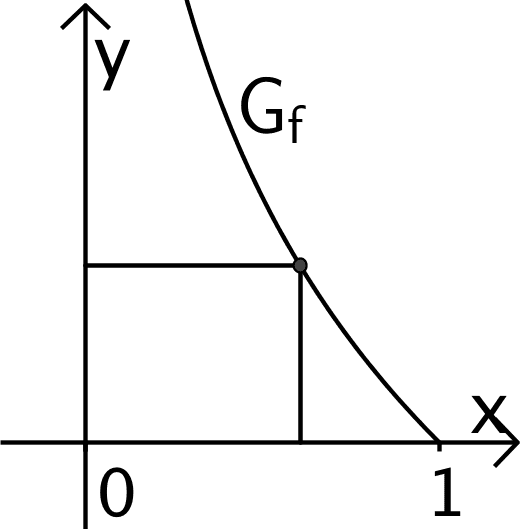Abb. 1
Unter den betrachteten Rechtecken gibt es eines mit größtem Flächeninhalt. Berechnen Sie die Seitenlängen dieses Rechtecks.
(5 BE)
- Details
- Kategorie: Analysis 2
Die Abbildung zeigt den Graphen einer Funktion \(f\).
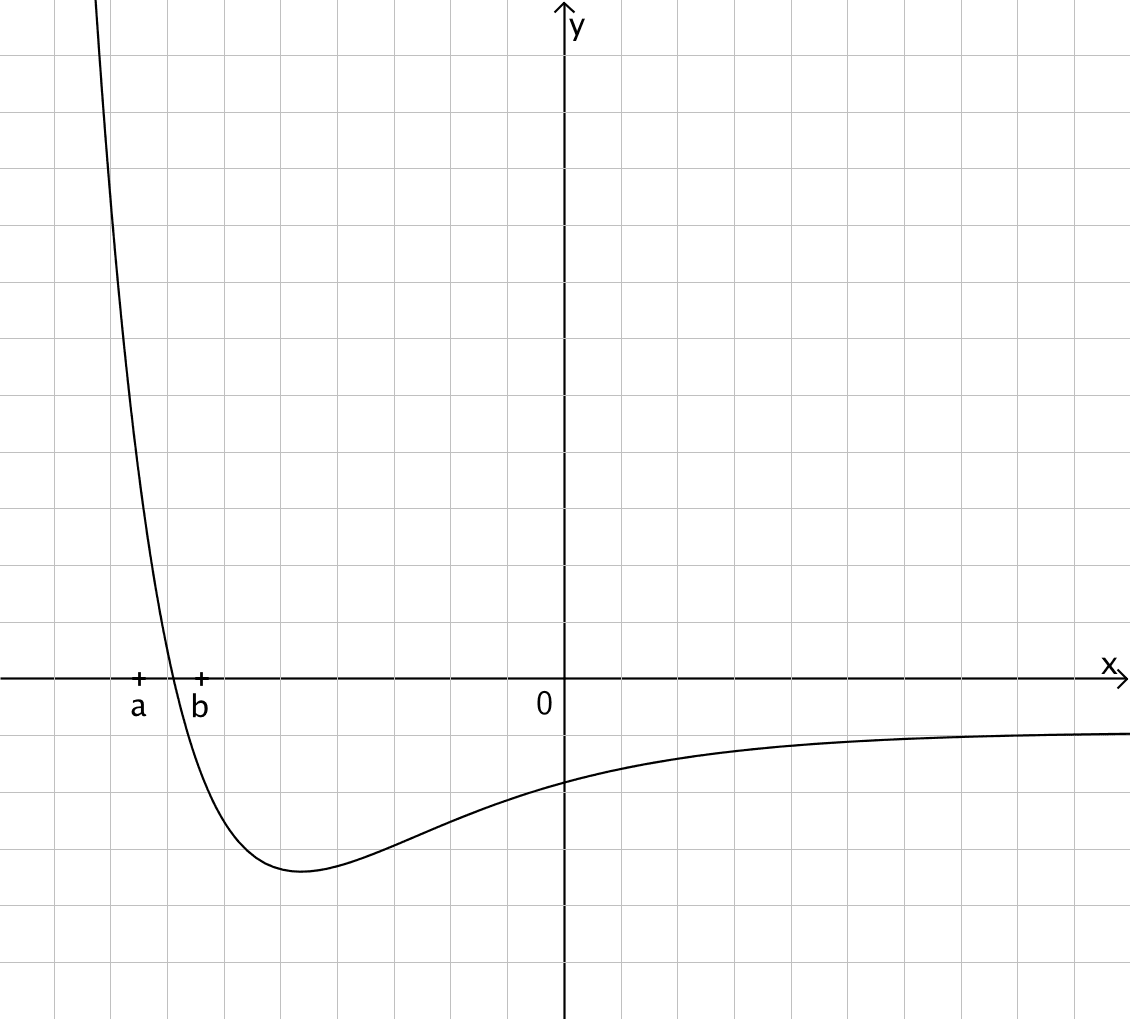Abb. 2
Beschreiben Sie für \(a \leq x \leq b\) den Verlauf des Graphen einer Stammfunktion von \(f\).
(2 BE)
- Details
- Kategorie: Analysis 2
Skizzieren Sie in der Abbildung den Graphen einer Stammfunktion von \(f\) im gesamten dargestellten Bereich.
(3 BE)
