Die von Solarmodulen abgegebene elektrische Leistung hängt unter anderem von der Größe ihres Neigungswinkels gegen die Horizontale ab. Die Tabelle gibt den Anteil der abgegebenen Leistung an der maximal möglichen Leistung in Abhängigkeit von der Größe des Neigungswinkels an. Schätzen Sie diesen Anteil für die Solarmodule des Pavillons - nach Berechnung des Neigungswinkels - unter Verwendung der Tabelle ab.

(4 BE)
Lösung zu Teilaufgabe 1e
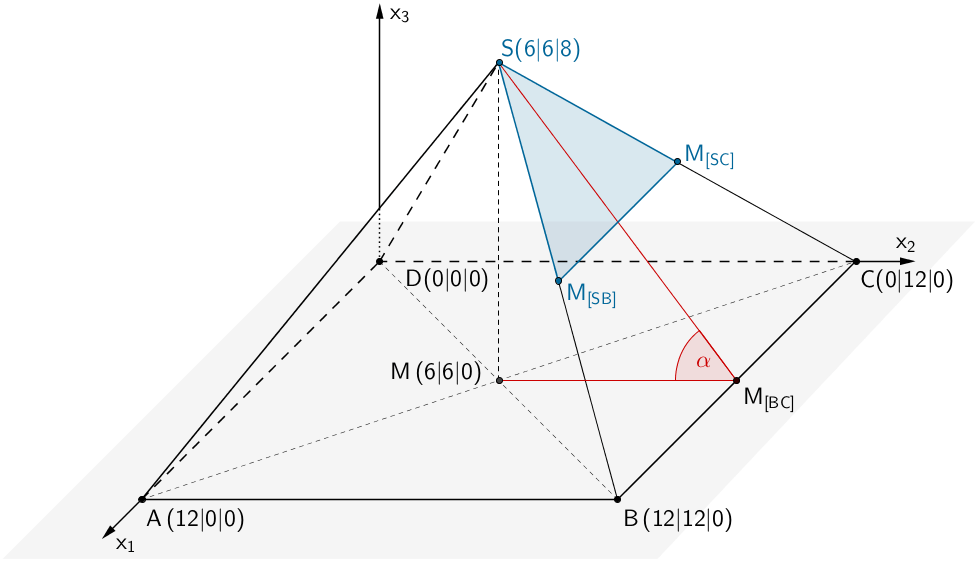
Die von den Solarmodulen bedeckte dreieckige Fläche \(M_{[SB]}M_{[SC]}S\) liegt in der Ebene \(E\) (siehe Teilaufgabe 1b). Der Neigungswinkel der Solarmodule gegen die Horizontale entspricht dem Schnittwinkel \(\alpha\) zwischen der Ebene \(E\) und der \(x_1x_2\)-Ebene.
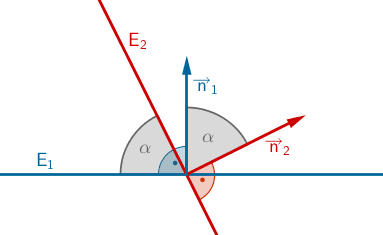
Schnittwinkel \(\boldsymbol{\alpha}\) zweier Ebenen
\[E_1\colon \enspace \overrightarrow{n}_1 \circ \left( \overrightarrow{X} - \overrightarrow{A} \right) = 0\]
\[E_2\colon \enspace \overrightarrow{n}_2 \circ \left( \overrightarrow{X} - \overrightarrow{B} \right) = 0\]
\[\cos \alpha = \frac{\vert \overrightarrow{n}_1 \circ \overrightarrow{n}_2 \vert}{\vert \overrightarrow{n}_1 \vert \cdot \vert \overrightarrow{n}_2 \vert} \enspace \Rightarrow \enspace \alpha = \cos^{-1}(\dots)\]
\[(0^{\circ} \leq \alpha \leq 90^{\circ})\]
\[E\,\colon\; 4x_2 + 3x_3 - 48 = 0\,; \quad \overrightarrow{n}_E = \begin{pmatrix} 0 \\ 4 \\ 3 \end{pmatrix}\]
\[x_1x_2\text{-Ebene}\,\colon\; x_3 = 0\,; \quad \overrightarrow{n}_{x_1x_2} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\]
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \cos{\alpha} &= \frac{\vert \overrightarrow{n}_E \circ \overrightarrow{n}_{x_1x_2} \vert}{\vert \overrightarrow{n}_E \vert \cdot \vert \overrightarrow{n}_{x_1x_2} \vert} \\[0.8em] &= \frac{\left| \begin{pmatrix} 0 \\ 4 \\ 3 \end{pmatrix} \circ \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right|}{\left| \begin{pmatrix} 0 \\ 4 \\ 3 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \right|} \\[0.8em] &= \frac{\vert 0 \cdot 0 + 4 \cdot 0 + 3 \cdot 1 \vert}{\sqrt{0^2 + 4^2 + 3^2} \cdot \sqrt{0^2 + 0^2 + 1^2}} \\[0.8em] &= \frac{3}{5} & &| \; \cos^{-1}(\dots) \\[0.8em] \alpha &= 53{,}13^{\circ} \end{align*}\]
Laut Tabelle liegt der Anteil der abgegebenen Leistung an der maximal möglichen Leistung der Solarmodule für einen Neigungswinkel von 53,13° zwischen 94 % und 98 %.

