In einem kartesischen Koordinatensystem legen die Punkte \(A\,(4|0|0)\), \(B\,(0|4|0)\) und \(C\,(0|0|4)\) das Dreieck \(ABC\) fest, das in der Ebene \(E\,\colon \, x_1 + x_2 + x_3 = 4\) liegt.
Bestimmen Sie den Flächeninhalt des Dreiecks \(ABC\).
(3 BE)
Lösung zu Teilaufgabe a
1. Lösungsansatz: Elementargeometrischer Ansatz
\[A\,(4|0|0)\,, \enspace B\,(0|4|0)\,, \enspace C\,(0|0|4)\]
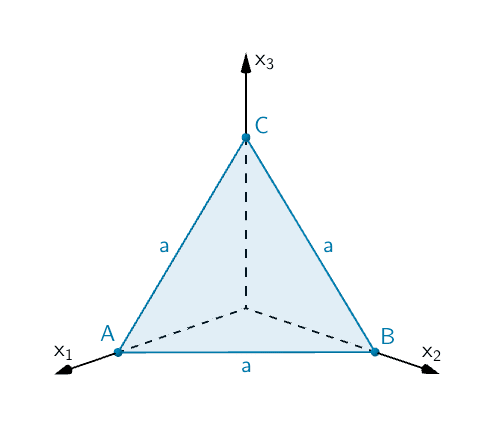
Da die Punkte \(A\), \(B\) und \(C\) jeweils auf einer Koordinatenachse bei 4 liegen, ist das Dreieck \(ABC\) gleichseitig.
Gleichseitiges Dreieck
\[\alpha = \beta = \gamma = 60^{\circ}\]
\[h = \frac{a}{2} \sqrt{3}\]
\[A = \frac{a^2}{4} \sqrt{3}\]
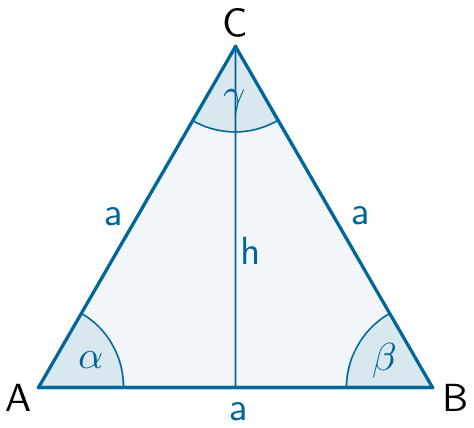
\[A_{\triangle ABC} = \frac{a^2}{4}\sqrt{3}\]
Seitenlänge \(a\) des gleichseitigen Dreiecks \(ABC\) berechnen:
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*}a &= \vert \overrightarrow{AB} \vert \\[0.8em] &= \vert \overrightarrow{B} - \overrightarrow{A} \vert \\[0.8em] &= \begin{pmatrix} 0 \\ 4 \\ 0 \end{pmatrix} - \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} -4 \\ 4 \\ 0 \end{pmatrix} \\[0.8em] &= \sqrt{(-4)^2 + 4^2 + 0^2} \\[0.8em] &= \sqrt{32} = 4\sqrt{2}\end{align*}\]
Flächeninhalt des Dreiecks \(ABC\) berechnen:
\[A_{\triangle ABC} = \frac{a^2}{4}\sqrt{3} = \frac{(4\sqrt{2})^2}{4}\sqrt{3} = \frac{32}{4}\sqrt{3} = 8\sqrt{3} \approx 13{,}86\]
Der Flächeninhalt des Dreiecks \(ABC\) beträgt 13,86 FE (Flächeneinheiten).
2. Lösungsansatz: Vektorprodukt anwenden
\[A\,(4|0|0)\,, \enspace B\,(0|4|0)\,, \enspace C\,(0|0|4)\]
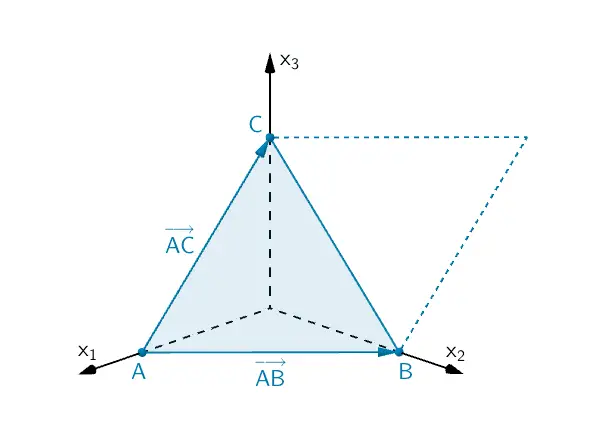
Die Vektoren \(\overrightarrow{AB}\) und \(\overrightarrow{AC}\) spannen ein Parallelogramm auf, dessen Flächeninhalt sich mit dem Vektorprodukt berechnen lässt. Der Flächeninhalt des Dreiecks \(ABC\) ist gleich dem halben Flächeninhalt des Parallelogramms.
Anwendung des Vekorprodukts
Der Betrag des Vektorprodukts \(\overrightarrow{a} \times \overrightarrow{b}\) entspricht der Maßzahl des Flächeninhalts eines von zwei Vektoren \(\overrightarrow{a} \neq \overrightarrow{0}\) und \(\overrightarrow{b} \neq \overrightarrow{0}\) aufgespannten Parallelogramms.
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \textcolor{#cc071e}{\vert \overrightarrow{b} \vert \cdot \sin{\varphi}}\]
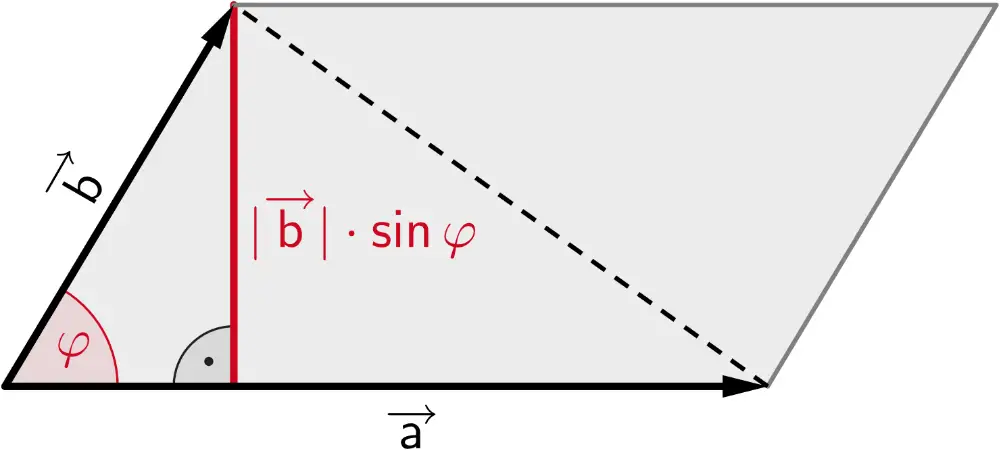
Flächeninhalt eines Parallelogramms
\[A = \vert \overrightarrow{a} \times \overrightarrow{b} \vert\]
Flächeninhalt eines Dreiecks
\[A = \frac{1}{2} \cdot \vert \overrightarrow{a} \times \overrightarrow{b} \vert\]
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*}A_{\triangle ABC} &= \frac{1}{2} \cdot \vert \overrightarrow{AB} \times \overrightarrow{AC} \vert \\[0.8em] &= \frac{1}{2} \cdot \vert (\overrightarrow{B} - \overrightarrow{A}) \times (\overrightarrow{C} - \overrightarrow{A}) \vert \\[0.8em] &= \frac{1}{2} \cdot \left| \left[\begin{pmatrix} 0 \\ 4 \\ 0 \end{pmatrix} - \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix} \right] \times \left[\begin{pmatrix} 0 \\ 0 \\ 4 \end{pmatrix} - \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix} \right] \right| \\[0.8em] &= \frac{1}{2} \cdot \left| \begin{pmatrix} -4 \\ 4 \\ 0 \end{pmatrix} \times \begin{pmatrix} -4 \\ 0 \\ 4 \end{pmatrix} \right| \\[0.8em] &= \frac{1}{2} \cdot \left| \begin{pmatrix} 4 & \cdot & 4 & - & 0 & \cdot & 0 \\ 0 & \cdot & (-4) & - & (-4) & \cdot & 4 \\ (-4) & \cdot & 0 & - & 4 & \cdot & (-4) \end{pmatrix} \right| \\[0.8em] &= \frac{1}{2} \cdot \left| \begin{pmatrix} 16 \\ 16 \\ 16 \end{pmatrix} \right| \\[0.8em] &= \frac{1}{2} \cdot \sqrt{16^2 + 16^2 + 16^2} \\[0.8em] &= \frac{1}{2} \cdot \sqrt{3 \cdot 16^2} \\[0.8em] &= \frac{1}{2} \cdot 16\sqrt{3} \\[0.8em] &= 8\sqrt{3} = 13{,}86 \end{align*}\]
Der Flächeninhalt des Dreiecks \(ABC\) beträgt 13,86 FE (Flächeneinheiten).


